
Concept explainers
(a)
The rest energy of Boson (W) in GeV if the mass of intermediate vector Boson
(a)
Answer to Problem 24Q
Solution:
80.27 GeV.
Explanation of Solution
Given data:
The mass of intermediate Boson is 85.6 times the mass of a proton.
Formula used:
Einstein proposed in his
Here, m is the mass and c is the
The conversion formula from joule to GeV is:
Explanation:
Consider the mass of protons to be
Recall the expression for energy.
Substitute
Conclusion:
The rest mass energy as given by Einstein’s equation is 80.27 GeV.
(b)
The rest energy of Boson (W) in GeV if the mass of intermediate vector Boson
(b)
Answer to Problem 24Q
Solution:
Explanation of Solution
Given data:
The mass of intermediate Boson is 85.6 times the mass of a proton.
Formula used:
Einstein proposed in his special theory of relativity that energy is also given as:
Here, m is the mass and c is the speed of light.
The energy and temperature relation is:
Here, k is the Boltzmann constant and T is the temperature.
Explanation:
If the rest mass of Boson is taken into consideration, the threshold temperature of the Bosons can be calculated.
Consider the Boltzmann constant to be
Recall the expression for energy and temperature.
Substitute
Conclusion:
The threshold temperature obtained is
(c)
The time after the Big Bang when Boson particles and antiparticles disappeared with the help of the below figure.
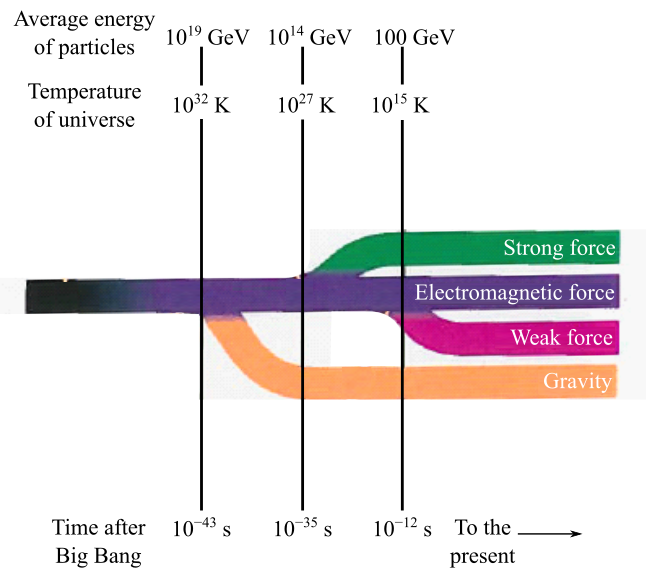
(c)
Answer to Problem 24Q
Solution:
Explanation of Solution
Introduction:
When the Big Bang occurred, all the forces bound together. As the temperature started to decrease with time, the forces got separated because the average temperature of the particles decreased.
Explanation:
From sub-part (a), the energy of the particle is 80.27 GeV and, from sub-part (b), the temperature is
So, from the figure, it can be inferred that the time for which the average energy of the particle is 80.27 GeV and the temperature is
Conclusion:
The time for which the temperature obtained is
Want to see more full solutions like this?
Chapter 26 Solutions
EBK LOOSE-LEAF VERSION OF UNIVERSE
- Exercise 1: (a) Using the explicit formulae derived in the lectures for the (2j+1) × (2j + 1) repre- sentation matrices Dm'm, (J/h), derive the 3 × 3 matrices corresponding to the case j = 1. (b) Verify that they satisfy the so(3) Lie algebra commutation relation: [D(Î₁/ħ), D(Î₂/h)]m'm₁ = iƊm'm² (Ĵ3/h). (c) Prove the identity 3 Dm'm,(β) = Σ (D(Ρ)D(Ρ))m'¡m; · i=1arrow_forwardSketch the harmonic.arrow_forwardFor number 11 please sketch the harmonic on graphing paper.arrow_forward
- # E 94 20 13. Time a) What is the frequency of the above wave? b) What is the period? c) Highlight the second cycle d) Sketch the sine wave of the second harmonic of this wave % 7 & 5 6 7 8 * ∞ Y U 9 0 0 P 150arrow_forwardShow work using graphing paperarrow_forwardCan someone help me answer this physics 2 questions. Thank you.arrow_forward
- Four capacitors are connected as shown in the figure below. (Let C = 12.0 μF.) a C 3.00 με Hh. 6.00 με 20.0 με HE (a) Find the equivalent capacitance between points a and b. 5.92 HF (b) Calculate the charge on each capacitor, taking AV ab = 16.0 V. 20.0 uF capacitor 94.7 6.00 uF capacitor 67.6 32.14 3.00 µF capacitor capacitor C ☑ με με The 3 µF and 12.0 uF capacitors are in series and that combination is in parallel with the 6 μF capacitor. What quantity is the same for capacitors in parallel? μC 32.14 ☑ You are correct that the charge on this capacitor will be the same as the charge on the 3 μF capacitor. μCarrow_forwardIn the pivot assignment, we observed waves moving on a string stretched by hanging weights. We noticed that certain frequencies produced standing waves. One such situation is shown below: 0 ст Direct Measurement ©2015 Peter Bohacek I. 20 0 cm 10 20 30 40 50 60 70 80 90 100 Which Harmonic is this? Do NOT include units! What is the wavelength of this wave in cm with only no decimal places? If the speed of this wave is 2500 cm/s, what is the frequency of this harmonic (in Hz, with NO decimal places)?arrow_forwardFour capacitors are connected as shown in the figure below. (Let C = 12.0 µF.) A circuit consists of four capacitors. It begins at point a before the wire splits in two directions. On the upper split, there is a capacitor C followed by a 3.00 µF capacitor. On the lower split, there is a 6.00 µF capacitor. The two splits reconnect and are followed by a 20.0 µF capacitor, which is then followed by point b. (a) Find the equivalent capacitance between points a and b. µF(b) Calculate the charge on each capacitor, taking ΔVab = 16.0 V. 20.0 µF capacitor µC 6.00 µF capacitor µC 3.00 µF capacitor µC capacitor C µCarrow_forward
- Two conductors having net charges of +14.0 µC and -14.0 µC have a potential difference of 14.0 V between them. (a) Determine the capacitance of the system. F (b) What is the potential difference between the two conductors if the charges on each are increased to +196.0 µC and -196.0 µC? Varrow_forwardPlease see the attached image and answer the set of questions with proof.arrow_forwardHow, Please type the whole transcript correctly using comma and periods as needed. I have uploaded the picture of a video on YouTube. Thanks,arrow_forward
 College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College
College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning University Physics Volume 3PhysicsISBN:9781938168185Author:William Moebs, Jeff SannyPublisher:OpenStax
University Physics Volume 3PhysicsISBN:9781938168185Author:William Moebs, Jeff SannyPublisher:OpenStax AstronomyPhysicsISBN:9781938168284Author:Andrew Fraknoi; David Morrison; Sidney C. WolffPublisher:OpenStax
AstronomyPhysicsISBN:9781938168284Author:Andrew Fraknoi; David Morrison; Sidney C. WolffPublisher:OpenStax Modern PhysicsPhysicsISBN:9781111794378Author:Raymond A. Serway, Clement J. Moses, Curt A. MoyerPublisher:Cengage Learning
Modern PhysicsPhysicsISBN:9781111794378Author:Raymond A. Serway, Clement J. Moses, Curt A. MoyerPublisher:Cengage Learning





