Chapter 26, Problem 1Q

Figure 26-15 shows cross sections through three long conductors of the same length and material, with square cross sections of edge lengths as shown. Conductor B fits snugly within conductor A, and conductor C fits snugly within conductor B. Rank the following according to their end-to-end resistances, greatest first: the individual conductors and the combinations of A + B (B inside A), B + C(C inside B), and A + B + C(B inside A inside C).

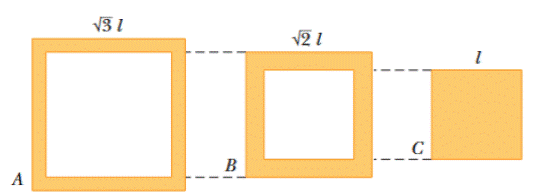
Figure 26-15 Question 1.

To determine

To find:

Ranking of resistances from greatest to lowest.

Answer to Problem 1Q

Solution:

Ranking of resistances from greatest to lowest is

$R_A+R_B+R_C>R_B+R_C=R_A+R_B>R_A=R_B=R_C$.

Explanation of Solution

1) Concept:

We use the formula of resistance related to resistivity, length, and area. Here, we have given the material and length as same for the given conductors, so the resistivity and length are same for all. So, the resistance will be proportional to only the area of cross section of the conductor. Using the proportionality relation, we can rank the resistances for given combinations.

2) Formula:

$R=\frac{\rho L}{A}$

3) Given:

Figure 26-15 is the cross sections of conductors.

4) Calculation:

We can calculate the area of cross section of each conductor as,

Area of conductor C is $l^2$ and conductor B is ${\left(\sqrt{2}l\right)}^2-l^2=2l^2-l^2=l^2$

Similarly, area of conductor A is ${\left(\sqrt{3}l\right)}^2-l^2-l^2= 3l^2-2l^2=l^2.$ This gives the area of cross section of the given conductors as the same.

We know the formula,

$R=\frac{\rho L}{A}$

Here, the given conductors are of same material and length so the resistivity and length are the same for each conductor, so the resistance depends on only the area of cross section of the conductor as,

$R\propto \frac{1}{A}\dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots .1)$

The resistancesof given combination of conductors are,

For combination of $A+B$ we get,

$R_A+R_B\propto \frac{1}{l^2}+\frac{1}{l^2}$

$R_A+R_B\propto \frac{2}{l^2}$

For $B+C$ we get,

$R_B+R_C\propto \frac{1}{l^2}+\frac{1}{l^2}$

$R_B+R_C\propto \frac{2}{l^2}$

For $A+B+C$ we get,

$R_A+R_B+R_C\propto \frac{1}{l^2}+\frac{1}{l^2}+\frac{1}{l^2}$

$R_A+R_B+R_C\propto \frac{3}{l^2}$

From this, we can rank the resistances from greatest to lowest as follows,

$R_A+R_B+R_C>R_B+R_C=R_A+R_B>R_A=R_B=R_C$

Conclusion:

We can rank the combination of conductors of same material and length according to the resistance from their area of cross section.