Chapter 2.6, Problem 14E

Cost for a Can This is a continuation of Exercises 12 and 13. Suppose now that we use different materials in making different parts of the can. The material for the side of the can costs $0.10 per square inch, and the material for both the top and bottom costs $0.05 per square inch.

a. Use a formula to express the cost C, in dollars, of the material for the can as a function of the radius r.

b. What radius should you use to make the least expensive can?

An Aluminum Can The cost of making a can is determined by how much aluminum A, in square inches, is needed to make it. This in turn depends on the radius r and the height h of the can, both measured in inches. You will need some basic facts about cans. See Figure 2.107.

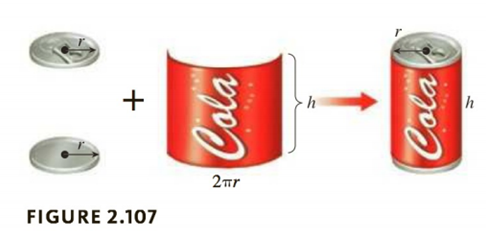
The surface of a can may be modeled as consisting of three parts: two circles of radius r and the surface of a cylinder of radius r and height h. The area of each circle is $\pi r^2$, In what follows, we assume that the can must hold 15 cubic inches, and we will look at various cans holding the same volume.

a. Explain why the height of any can that holds a volume of 15 cubic inches is given by $h=\frac{15}{\pi r^2}$

b. Make a graph of the height h as a function of r, and explain what the graph is showing.

c. Is there a value of r that gives the least height h? Explain.

d. If A is the amount of aluminum needed to make the can, explain why $A=2\pi r^2+2\pi rh$.

e. Using the formula for h from part a, explain why we may also write A as $A=2\pi r^2+\frac{30}{r}$.

An Aluminum Can, Continued This is a continuation of Exercise 12. The cost of making a can is determined by how much aluminum A, in square inches, is needed to make it. As we saw in Exercise 10, we can express both the height h and the amount of aluminum A in terms of the radius r:

$\begin{array}{l}h=\frac{15}{\pi r^2}\\ A=2\pi r^2+\frac{30}{r}\end{array}$

a. What is the height, and how much aluminum is needed to make the can, if the radius is 1 inch? (This is a tall, thin can.)

b. What is the height, and how much aluminum is needed to make the can, if the radius is 5 inches? (This is a short, fat can.)

c. The first two parts of this problem are designed to illustrate that for an aluminum can, different surface areas can enclose the same volume of 15 cubic inches.

i. Make a graph of A versus r and explain what the graph is showing.

ii. What radius should you use to make the can using the least amount of aluminum?

iii. What is the height of the can that uses the least amount of aluminum?