Chapter 2.6, Problem 11E

Refer to Exercise 9.

1. a. Find the conditional probability mass function p_Y|X(y | 4).
2. b. Find the conditional probability mass function p_X|Y(x | 3).
3. c. Find the conditional expectation E(Y | X =4).
4. d. Find the conditional expectation E(X | Y = 3).

9.    Bolts manufactured for a certain purpose may be classified as acceptable (suitable for the intended purpose), downgraded (unsuitable for the intended purpose but acceptable for a different purpose), or scrap (unsuitable for any purpose). In a lot of 500 bolts, let X be the number that are downgraded and let Y be the number that are scrap. Assume that the joint probability mass function of X and Y is given in the following table.

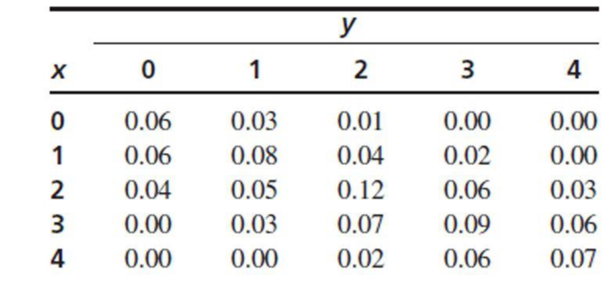
1. a. Find the marginal probability mass function of X.
2. b. Find the marginal probability mass function of Y.
3. c. Are X and Y independent? Explain.
4. d. Find μ_X and μ_Y.
5. e. Find σ_X and σ_Y.
6. f. Find Cov(X, Y).
7. g. Find ρ(X, Y).

To determine

Find the conditional probability mass function $p_{Y|X}\left(y|4\right)$.

Answer to Problem 11E

The conditional probability mass function $p_{Y|X}\left(y|4\right)$ is,

y	$p_{Y|X}\left(y|4\right)$
0	0
1	0
2	$\frac{2}{15}$
3	$\frac{2}{5}$
4	$\frac{7}{15}$

Explanation of Solution

Given info:

In a lot of 500 bolts, X be the number that are downgraded and Y be the number that are scrap.

Calculation:

The joint probability mass function of X and Y their totals are given in the following table:

		Y
X	0	1	2	3	4	Total
0	0.06	0.03	0.01	0.00	0.00	0.10
1	0.06	0.08	0.04	0.02	0.00	0.20
2	0.04	0.05	0.12	0.06	0.03	0.30
3	0.00	0.03	0.07	0.09	0.06	0.25
4	0.00	0.00	0.02	0.06	0.07	0.15
Total	0.16	0.19	0.26	0.23	0.16	1

Table 1

The formula for finding the conditional probability mass function can be written as,

$p_{Y|X}\left(y|x\right)=\frac{p_{X,Y}\left(x,y\right)}{p_X\left(x\right)}$

For $\left(x=4,y=0\right)$:

The conditional probability mass function for $\left(x=4,y=0\right)$ is,

$p_{Y|X}\left(0|4\right)=\frac{p_{X,Y}\left(4,0\right)}{p_X\left(4\right)}$

Substitute $p_{X,Y}\left(4,0\right)=0.00$ and $p_X\left(4\right)=0.15$

$\begin{array}{c}{p}_{Y|X}\left(0|4\right)=\frac{0.00}{0.15}\\ =0\end{array}$

For $\left(x=4,y=1\right)$:

The conditional probability mass function for $\left(x=4,y=1\right)$ is,

$p_{Y|X}\left(1|4\right)=\frac{p_{X,Y}\left(4,1\right)}{p_X\left(4\right)}$

Substitute $p_{X,Y}\left(4,1\right)=0.00$ and $p_X\left(4\right)=0.15$

$\begin{array}{c}{p}_{Y|X}\left(1|4\right)=\frac{0.00}{0.15}\\ =0\end{array}$

For $\left(x=4,y=2\right)$:

The conditional probability mass function for $\left(x=4,y=2\right)$ is,

$p_{Y|X}\left(2|4\right)=\frac{p_{X,Y}\left(4,2\right)}{p_X\left(4\right)}$

Substitute $p_{X,Y}\left(4,2\right)=0.02$ and $p_X\left(4\right)=0.15$

$\begin{array}{c}{p}_{Y|X}\left(2|4\right)=\frac{0.02}{0.15}\\ =\frac{2}{5}\end{array}$

For $\left(x=4,y=3\right)$:

The conditional probability mass function for $\left(x=4,y=3\right)$ is,

$p_{Y|X}\left(3|4\right)=\frac{p_{X,Y}\left(4,3\right)}{p_X\left(4\right)}$

Substitute $p_{X,Y}\left(4,3\right)=0.06$ and $p_X\left(4\right)=0.15$

$\begin{array}{c}{p}_{Y|X}\left(3|4\right)=\frac{0.06}{0.15}\\ =\frac{2}{5}\end{array}$

For $\left(x=4,y=4\right)$:

The conditional probability mass function for $\left(x=4,y=4\right)$ is,

$p_{Y|X}\left(1|4\right)=\frac{p_{X,Y}\left(4,1\right)}{p_X\left(4\right)}$

Substitute $p_{X,Y}\left(4,4\right)=0.07$ and $p_X\left(4\right)=0.15$

$\begin{array}{c}{p}_{Y|X}\left(4|4\right)=\frac{0.07}{0.15}\\ =\frac{7}{15}\end{array}$

Thus, the conditional probability mass function $p_{Y|X}\left(y|4\right)$ is,

y	$p_{Y|X}\left(y|4\right)$
0	0
1	0
2	$\frac{2}{15}$
3	$\frac{2}{5}$
4	$\frac{7}{15}$

To determine

Find the conditional probability mass function $p_{X|Y}\left(x|3\right)$.

Answer to Problem 11E

The conditional probability mass function $p_{X|Y}\left(x|3\right)$ is,

x	$p_{X|Y}\left(x|3\right)$
0	0
1	$\frac{2}{23}$
2	$\frac{6}{23}$
3	$\frac{9}{23}$
4	$\frac{6}{23}$

Explanation of Solution

Calculation:

The formula for finding the conditional probability mass function can be written as,

$p_{X|Y}\left(x|y\right)=\frac{p_{X,Y}\left(x,y\right)}{p_Y\left(y\right)}$

For $\left(x=0,y=3\right)$:

The conditional probability mass function for $\left(x=0,y=3\right)$ is,

$p_{X|Y}\left(0|3\right)=\frac{p_{X,Y}\left(0,3\right)}{p_Y\left(3\right)}$

Substitute $p_{X,Y}\left(0,3\right)=0.00$ and $p_Y\left(3\right)=0.23$

$\begin{array}{c}{p}_{X|Y}\left(0|3\right)=\frac{0.00}{0.23}\\ =0\end{array}$

For $\left(x=1,y=3\right)$:

The conditional probability mass function for $\left(x=1,y=3\right)$ is,

$p_{X|Y}\left(1|3\right)=\frac{p_{X,Y}\left(1,3\right)}{p_Y\left(3\right)}$

Substitute $p_{X,Y}\left(1,3\right)=0.02$ and $p_Y\left(3\right)=0.23$

$\begin{array}{c}{p}_{X|Y}\left(1|3\right)=\frac{0.02}{0.23}\\ =\frac{2}{23}\end{array}$

For $\left(x=2,y=3\right)$:

The conditional probability mass function for $\left(x=2,y=3\right)$ is,

$p_{X|Y}\left(2|3\right)=\frac{p_{X,Y}\left(2,3\right)}{p_Y\left(3\right)}$

Substitute $p_{X,Y}\left(2,3\right)=0.06$ and $p_Y\left(3\right)=0.23$

$\begin{array}{c}{p}_{X|Y}\left(2|3\right)=\frac{0.06}{0.23}\\ =\frac{6}{23}\end{array}$

For $\left(x=3,y=3\right)$:

The conditional probability mass function for $\left(x=3,y=3\right)$ is,

$p_{X|Y}\left(3|3\right)=\frac{p_{X,Y}\left(3,3\right)}{p_Y\left(3\right)}$

Substitute $p_{X,Y}\left(3,3\right)=0.09$ and $p_Y\left(3\right)=0.23$

$\begin{array}{c}{p}_{X|Y}\left(3|3\right)=\frac{0.09}{0.23}\\ =\frac{9}{23}\end{array}$

For $\left(x=4,y=3\right)$:

The conditional probability mass function for $\left(x=4,y=3\right)$ is,

$p_{X|Y}\left(4|3\right)=\frac{p_{X,Y}\left(4,3\right)}{p_Y\left(3\right)}$

Substitute $p_{X,Y}\left(4,3\right)=0.06$ and $p_Y\left(3\right)=0.23$

$\begin{array}{c}{p}_{X|Y}\left(4|3\right)=\frac{0.06}{0.23}\\ =\frac{6}{23}\end{array}$

Thus, the conditional probability mass function $p_{X|Y}\left(x|3\right)$ is,

x	$p_{X|Y}\left(x|3\right)$
0	0
1	$\frac{2}{23}$
2	$\frac{6}{23}$
3	$\frac{9}{23}$
4	$\frac{6}{23}$

To determine

Find the conditional expectation $E\left(Y|X=4\right)$.

Answer to Problem 11E

The conditional expectation $E\left(Y|X=4\right)$ is 3.33.

Explanation of Solution

Calculation:

The formula for finding the conditional expectation $E\left(Y|X=4\right)$ is,

$\begin{array}{c}E\left(Y|X=4\right)={\displaystyle \sum y{p}_{Y|X}\left(y|4\right)}\\ =0p_{Y|X}\left(0|4\right)+1p_{Y|X}\left(1|4\right)+2p_{Y|X}\left(2|4\right)+3p_{Y|X}\left(3|4\right)+4p_{Y|X}\left(4|4\right)\\ =0\left(0\right)+1\left(0\right)+2\left(\frac{2}{15}\right)+3\left(\frac{2}{5}\right)+4\left(\frac{7}{15}\right)\\ =\frac{4}{15}+\frac{6}{5}+\frac{28}{15}\\ =3.33\end{array}$

Thus, the conditional expectation $E\left(Y|X=4\right)$ is 3.33.

To determine

Find the conditional expectation $E\left(X|Y=3\right)$.

Answer to Problem 11E

The conditional expectation $E\left(X|Y=3\right)$ is 2.83.

Explanation of Solution

Calculation:

The formula for finding the conditional expectation $E\left(X|Y=3\right)$ is,

$\begin{array}{c}E\left(X|Y=3\right)={\displaystyle \sum x{p}_{X|Y}\left(x|3\right)}\\ =0p_{X|Y}\left(0|3\right)+1p_{X|Y}\left(1|3\right)+2p_{X|Y}\left(2|3\right)+3p_{X|Y}\left(3|3\right)+4p_{X|Y}\left(4|3\right)\\ =0\left(0\right)+1\left(\frac{2}{23}\right)+2\left(\frac{6}{23}\right)+3\left(\frac{9}{23}\right)+4\left(\frac{6}{23}\right)\\ =\frac{65}{23}\\ =2.83\end{array}$

Thus, the conditional expectation $E\left(X|Y=2\right)$ is $\frac{19}{22}$.