
Concept explainers
(a)
The proof for
(a)
Answer to Problem 71CP
The electric potential at the point
Explanation of Solution
The following figure shows the diagram of the dipoles and the point
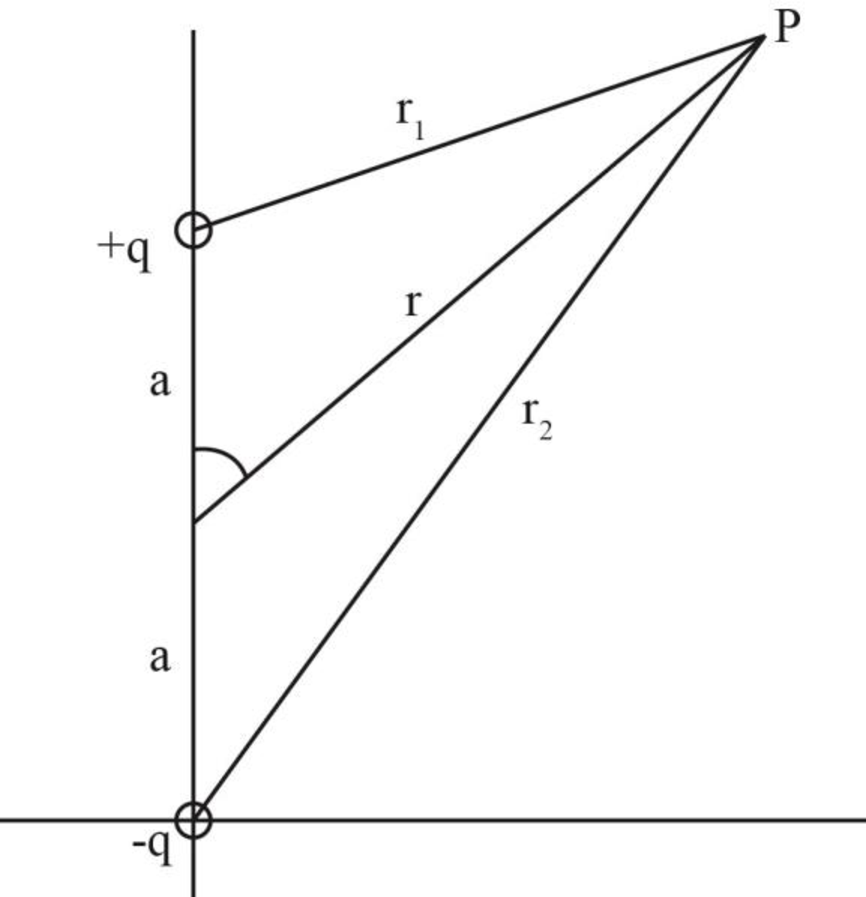
Figure-(1)
The dipole moment’s magnitude is given as.
Here,
Write the equation for the electric potential at the point
Here,
Write the equation for the distance between the positive charge and the point
Write the equation for the distance between the negative charge and the point
Rearrange the equation (II) and (III) to calculate
Expand the above equation binomially and neglect the higher terms to calculate
Substitute
Substitute
Therefore, the electric potential at the point
(b)
The electric field’s radial component
(b)
Answer to Problem 71CP
The electric field’s radial component is
Explanation of Solution
Write the equation for the radial component of the electric field.
Here,
Write the equation for the perpendicular component of the electric field.
Here,
Conclusion:
Substitute
Substitute
Therefore, the electric field’s radial component is
(c)
Whether the results for
(c)
Answer to Problem 71CP
Yes, the results for
Explanation of Solution
Write the equation for
Write the equation for
Conclusion:
Substitute
Substitute
Substitute
Substitute
Therefore, the results for
(d)
Whether the results for
(d)
Answer to Problem 71CP
No, the results for
Explanation of Solution
Write the equation for
Write the equation for
Conclusion:
Substitute
Substitute
Therefore, the results for
(e)
The expression for the electric potential in terms of the Cartesian coordinates.
(e)
Answer to Problem 71CP
The expression for the electric potential in terms of the Cartesian coordinates is
Explanation of Solution
Write the equation for the electric potential.
Conclusion:
Substitute
Therefore, the expression for the electric potential in terms of the Cartesian coordinates is
(f)
The
(f)
Answer to Problem 71CP
The
Explanation of Solution
Write the equation for the
Here,
Write the equation for the
Here,
Conclusion:
Substitute
Substitute
Therefore, the
Want to see more full solutions like this?
Chapter 25 Solutions
Physics For Scientists And Engineers With Modern Physics, 9th Edition, The Ohio State University
- Hi Expert in Physics, Could you please Rewrite thses random equations using good formula of mathematics and explain each Greek alphabet and their meaning in English? Best Regards, Yahyaarrow_forwardHi Expert, I have uploaded picture, could you please name the Greek alphabet and their name in English?arrow_forwardHi Expert in Physics, I have uploaded pictures with respect to some physics equations. Could please name all Greek alphabet and their English name?arrow_forward
- 81 SSM Figure 29-84 shows a cross section of an infinite conducting sheet carrying a current per unit x-length of 2; the current emerges perpendicularly out of the page. (a) Use the Biot-Savart law and symmetry to show that for all points B P P. BD P' Figure 29-84 Problem 81. x P above the sheet and all points P' below it, the magnetic field B is parallel to the sheet and directed as shown. (b) Use Ampere's law to prove that B = ½µλ at all points P and P'.arrow_forwardWhat All equations of Ountum physics?arrow_forwardPlease rewrite the rules of Quantum mechanics?arrow_forward
- Suppose there are two transformers between your house and the high-voltage transmission line that distributes the power. In addition, assume your house is the only one using electric power. At a substation the primary of a step-down transformer (turns ratio = 1:23) receives the voltage from the high-voltage transmission line. Because of your usage, a current of 51.1 mA exists in the primary of the transformer. The secondary is connected to the primary of another step-down transformer (turns ratio = 1:36) somewhere near your house, perhaps up on a telephone pole. The secondary of this transformer delivers a 240-V emf to your house. How much power is your house using? Remember that the current and voltage given in this problem are rms values.arrow_forwardThe human eye is most sensitive to light having a frequency of about 5.5 × 1014 Hz, which is in the yellow-green region of the electromagnetic spectrum. How many wavelengths of this light can fit across a distance of 2.2 cm?arrow_forwardA one-dimensional harmonic oscillator of mass m and angular frequency w is in a heat bath of temperature T. What is the root mean square of the displacement of the oscillator? (In the expressions below k is the Boltzmann constant.) Select one: ○ (KT/mw²)1/2 ○ (KT/mw²)-1/2 ○ kT/w O (KT/mw²) 1/2In(2)arrow_forward
- Two polarizers are placed on top of each other so that their transmission axes coincide. If unpolarized light falls on the system, the transmitted intensity is lo. What is the transmitted intensity if one of the polarizers is rotated by 30 degrees? Select one: ○ 10/4 ○ 0.866 lo ○ 310/4 01/2 10/2arrow_forwardBefore attempting this problem, review Conceptual Example 7. The intensity of the light that reaches the photocell in the drawing is 160 W/m², when 0 = 18°. What would be the intensity reaching the photocell if the analyzer were removed from the setup, everything else remaining the same? Light Photocell Polarizer Insert Analyzerarrow_forwardThe lifetime of a muon in its rest frame is 2.2 microseconds. What is the lifetime of the muon measured in the laboratory frame, where the muon's kinetic energy is 53 MeV? It is known that the rest energy of the muon is 106 MeV. Select one: O 4.4 microseconds O 6.6 microseconds O 3.3 microseconds O 1.1 microsecondsarrow_forward
 Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
 Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College
College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College





