
a.
To construct: The 95% confidence interval for the proportion of students who have used drugs more than one time in a given month to stay awake.
a.
Answer to Problem 25.32E
The 95% confidence interval for the proportion of students who have used drugs more than one time in a given month to stay awake is 0.173695 to 0.227894.
Explanation of Solution
Given info:
The data shows the association between the sleep quality classification and the use of over-the-counter (OTC) or prescription (RX) stimulant medication more than once a month to help keep them awake.
Calculation:
Let
Thus, the proportion of students who have used drugs more than one time in a given month to stay awake is 0.1998.
Software procedure:
Step-by-step procedure for constructing 95% confidence interval for the given proportion is shown below:
- Click on Stat, Basic statistics and 1-proportion.
- Choose Summarized data, under Number of
events enter 174, under Number of trials enter 871. - Click on options, choose 95% confidence interval.
- Click ok.
Output using MINITAB is given below:

Conclusion:
The 95% confidence interval for the proportion of students who have used drugs more than one time in a given month to stay awake is 0.173695 to 0.227894.
b.
To find: The conditional distribution for the sleep quality of the students who have used drugs and those who haven’t.
To construct: A graph that compares the two conditional distributions.
To describe: The relationship between the students who have used drugs to stay awake and students who haven’t used drugs to stay awake.
b.
Answer to Problem 25.32E
The conditional distribution for the sleep quality of the students who have used the drugs and those who haven’t used the drugs is given below:
| Sleep Quality | Conditional distributionof sleep quality for students who have used drugs | Conditional distribution of sleep quality for students who haven’t used drugs |
| Optimal | 12.2 | 87.8 |
| Borderline | 22.2 | 77.8 |
| Poor | 25.5 | 74.5 |
Output obtained from MINITAB is given below:
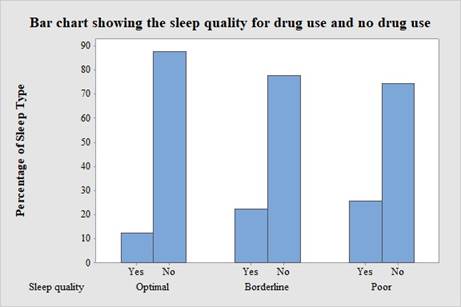
The students who have consumed drugs have less amount of optimal sleep than students who haven’t consumed drugs. Thus, consuming drugs helps the students to stay awake.
Explanation of Solution
Calculation:
The conditional distribution for the sleep quality of the students who have used the drugs is calculated as follows:
The conditional distribution for the sleep quality of the students who haven’t used the drugs is calculated as follows:
The two conditional distributions are given below:
| Sleep Quality | Conditional distributionof sleep quality for students who have used drugs | Conditional distribution of sleep quality for students who haven’t used drugs |
| Optimal | ||
| Borderline | ||
| Poor |
Software procedure:
Step-by-step procedure for constructing a bar graph for comparing the two conditional distributions is given below:
- Click on Graph, select Bar Chart.
- Under Bar represent: select Values from table.
- In Two-way table select Cluster and then click ok.
- In Graph variables, enter the columns of Yes and No.
- In Row labels, select Sleep quality.
- Under Table Arrangement, select Rows are outermost categories and columns are innermost.
- Click ok.
Interpretation:
The bar graph is constructed for the conditional distributions of sleep quality for students who have used drugs and students who haven’t used the drugs.
The bars are separated into three sets; the bars to the leftmost side represent the “Optimal” sleep quality, the bars placed in the middle represent the “Borderline” sleep quality, and the bars placed to the rightmost side represent the “Poor” sleep quality.
Justification:
From the conditional distributions and the bar graph, it can be observed that students who have consumed drugs have less amount of optimal sleep than students who haven’t consumed drugs.
Thus, consuming drugs help the students to stay awake.
c.
To test: Whether students who use drugs more than one time in a month to stay awake have a difference in sleep quality than the students who don’t use drugs.
To state: The hypotheses used for testing.
To give: The P-value and the conclusion.
c.
Answer to Problem 25.32E
There is a significant difference in the sleep quality between the students who have used the drugs and the students who don’t use drugs.
The hypotheses used for testing is given below:
The P-value is 0.000.
The drugs help the students to stay awake.
Explanation of Solution
Calculation:
The claim is to test whether there is any significant difference between the sleep quality of the students who have used the drugs and students who haven’t used the drugs.
Cell frequency for using Chi-square test:
- When at most 20% of the cell frequencies are less than 5
- If all the individual frequencies are 1 or more than 1.
- All the expected frequencies must be 5 or greater than 5.
The hypotheses used for testing is given below:
Software procedure:
Step-by-step procedure for calculating the chi-square test statistic is given below:
- Click on Stat, select Tables and then click on Chi-square Test of Association.
- Select Summarized data in a two-way table.
- Under Columns containing the table: enter the columns of Optimal, Borderline and Poor.
- Under Labels for the table (optional), select Drug Usage in the Rows: box and type Sleep Quality for the Column category name.
- Under statistics, click on Chi-square test.
- Click on ok.
Output obtained from MINITAB is given below:
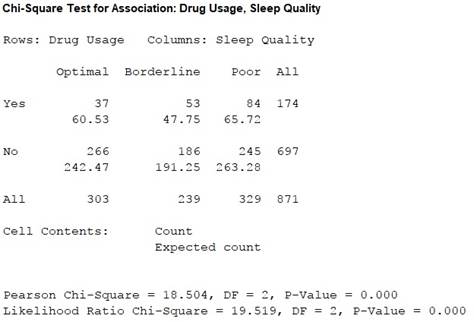
Thus, the test statistic is 18.504 and the P-value is 0.000.
Since all the expected frequencies are greater than 5,the usage of chi-square test is appropriate.
Conclusion:
The P-value is 0.000 and the level of significance is 0.05.
Here, the P-value is lesser than the level of significance.
Therefore, the null hypothesis is rejected.
Thus, there is strong evidence that there is a relationship between the sleep quality and drug usage.
Hence, students who have used the drugs have a low level of optimal sleep thanthe students who didn’t use the drugs. Thus, drugs help the students to stay awake.
Want to see more full solutions like this?
Chapter 25 Solutions
Loose-leaf Version for The Basic Practice of Statistics 7e & LaunchPad (Twelve Month Access)
- Pls help asaparrow_forwardSolve the following LP problem using the Extreme Point Theorem: Subject to: Maximize Z-6+4y 2+y≤8 2x + y ≤10 2,y20 Solve it using the graphical method. Guidelines for preparation for the teacher's questions: Understand the basics of Linear Programming (LP) 1. Know how to formulate an LP model. 2. Be able to identify decision variables, objective functions, and constraints. Be comfortable with graphical solutions 3. Know how to plot feasible regions and find extreme points. 4. Understand how constraints affect the solution space. Understand the Extreme Point Theorem 5. Know why solutions always occur at extreme points. 6. Be able to explain how optimization changes with different constraints. Think about real-world implications 7. Consider how removing or modifying constraints affects the solution. 8. Be prepared to explain why LP problems are used in business, economics, and operations research.arrow_forwardged the variance for group 1) Different groups of male stalk-eyed flies were raised on different diets: a high nutrient corn diet vs. a low nutrient cotton wool diet. Investigators wanted to see if diet quality influenced eye-stalk length. They obtained the following data: d Diet Sample Mean Eye-stalk Length Variance in Eye-stalk d size, n (mm) Length (mm²) Corn (group 1) 21 2.05 0.0558 Cotton (group 2) 24 1.54 0.0812 =205-1.54-05T a) Construct a 95% confidence interval for the difference in mean eye-stalk length between the two diets (e.g., use group 1 - group 2).arrow_forward
- An article in Business Week discussed the large spread between the federal funds rate and the average credit card rate. The table below is a frequency distribution of the credit card rate charged by the top 100 issuers. Credit Card Rates Credit Card Rate Frequency 18% -23% 19 17% -17.9% 16 16% -16.9% 31 15% -15.9% 26 14% -14.9% Copy Data 8 Step 1 of 2: Calculate the average credit card rate charged by the top 100 issuers based on the frequency distribution. Round your answer to two decimal places.arrow_forwardPlease could you check my answersarrow_forwardLet Y₁, Y2,, Yy be random variables from an Exponential distribution with unknown mean 0. Let Ô be the maximum likelihood estimates for 0. The probability density function of y; is given by P(Yi; 0) = 0, yi≥ 0. The maximum likelihood estimate is given as follows: Select one: = n Σ19 1 Σ19 n-1 Σ19: n² Σ1arrow_forward
- Please could you help me answer parts d and e. Thanksarrow_forwardWhen fitting the model E[Y] = Bo+B1x1,i + B2x2; to a set of n = 25 observations, the following results were obtained using the general linear model notation: and 25 219 10232 551 XTX = 219 10232 3055 133899 133899 6725688, XTY 7361 337051 (XX)-- 0.1132 -0.0044 -0.00008 -0.0044 0.0027 -0.00004 -0.00008 -0.00004 0.00000129, Construct a multiple linear regression model Yin terms of the explanatory variables 1,i, x2,i- a) What is the value of the least squares estimate of the regression coefficient for 1,+? Give your answer correct to 3 decimal places. B1 b) Given that SSR = 5550, and SST=5784. Calculate the value of the MSg correct to 2 decimal places. c) What is the F statistics for this model correct to 2 decimal places?arrow_forwardCalculate the sample mean and sample variance for the following frequency distribution of heart rates for a sample of American adults. If necessary, round to one more decimal place than the largest number of decimal places given in the data. Heart Rates in Beats per Minute Class Frequency 51-58 5 59-66 8 67-74 9 75-82 7 83-90 8arrow_forward
- can someone solvearrow_forwardQUAT6221wA1 Accessibility Mode Immersiv Q.1.2 Match the definition in column X with the correct term in column Y. Two marks will be awarded for each correct answer. (20) COLUMN X Q.1.2.1 COLUMN Y Condenses sample data into a few summary A. Statistics measures Q.1.2.2 The collection of all possible observations that exist for the random variable under study. B. Descriptive statistics Q.1.2.3 Describes a characteristic of a sample. C. Ordinal-scaled data Q.1.2.4 The actual values or outcomes are recorded on a random variable. D. Inferential statistics 0.1.2.5 Categorical data, where the categories have an implied ranking. E. Data Q.1.2.6 A set of mathematically based tools & techniques that transform raw data into F. Statistical modelling information to support effective decision- making. 45 Q Search 28 # 00 8 LO 1 f F10 Prise 11+arrow_forwardStudents - Term 1 - Def X W QUAT6221wA1.docx X C Chat - Learn with Chegg | Cheg X | + w:/r/sites/TertiaryStudents/_layouts/15/Doc.aspx?sourcedoc=%7B2759DFAB-EA5E-4526-9991-9087A973B894% QUAT6221wA1 Accessibility Mode பg Immer The following table indicates the unit prices (in Rands) and quantities of three consumer products to be held in a supermarket warehouse in Lenasia over the time period from April to July 2025. APRIL 2025 JULY 2025 PRODUCT Unit Price (po) Quantity (q0)) Unit Price (p₁) Quantity (q1) Mineral Water R23.70 403 R25.70 423 H&S Shampoo R77.00 922 R79.40 899 Toilet Paper R106.50 725 R104.70 730 The Independent Institute of Education (Pty) Ltd 2025 Q Search L W f Page 7 of 9arrow_forward
 MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc
MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning
Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning
Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON
Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman
The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman
Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman





