
Concept explainers
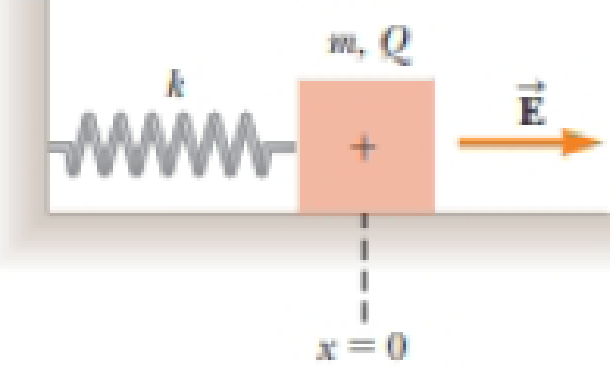
Review. A block having mass m and charge + Q is connected to an insulating spring having a force constant k. The block lies on a frictionless, insulating, horizontal track, and the system is immersed in a uniform electric field of magnitude E directed as shown in Figure P24.6. The block is released from rest when the spring is unstretched (at x = 0). We wish to show that the ensuing motion of the block is simple harmonic. (a) Consider the system of the block, the spring, and the electric field. Is this system isolated or nonisolated? (b) What kinds of potential energy exist within this system? (c) Call the initial configuration of the system that existing just as the block is released from rest. The final configuration is when the block momentarily comes to rest again. What is the value of x when the block comes to rest momentarily? (d) At some value of x we will call x = x0, the block has zero net force on it. What analysis model describes the particle in this situation? (c) What is the value of x0? (f) Define a new coordinate system x′ such that x′ = x − x0. Show that x′ satisfies a differential equation for
Figure P24.6
(a)
Whether the system is isolated or non-isolated.
Answer to Problem 6P
The system is non-isolated.
Explanation of Solution
Given info: The mass of the block is
The system of the block with a spring is isolated system but when the system of the block with a spring is placed in a electric or magnetic field then it experiences an external force that makes the system non-isolated.
Conclusion:
Therefore, the system is non-isolated.
(b)
The kinds of potential energy exist in the system.
Answer to Problem 6P
The kinds of potential energy exist in the system are elastic potential energy and electrostatic potential energy.
Explanation of Solution
Given info: The mass of the block is
There are two kinds of potential energy exist in the system one is elastic potential energy and other is electrostatic potential energy.
The formula to calculate the elastic potential energy is,
Here,
The formula to calculate the electrostatic potential energy is,
Here,
The formula to calculate electrostatic force is,
Here,
Substitute
Conclusion:
Therefore, the kinds of potential energy exist in the system are elastic potential energy and electrostatic potential energy.
(c)
The value of
Answer to Problem 6P
The value of
Explanation of Solution
Given info: The mass of the block is
The formula to calculate the elastic potential energy is,
Here,
The formula to calculate the electrostatic potential energy is,
Here,
The formula to calculate electrostatic force is,
Here,
Substitute
Equate the formula (1) and (2) as,
Conclusion:
Therefore, the value of
(d)
The analysis model that describes particle in this situation.
Answer to Problem 6P
The analysis model that describes the particle in this situation is in equilibrium.
Explanation of Solution
Given info: The mass of the block is
The above statement is explained as the net force acting on the block is zero at some value of
Conclusion:
Therefore, the particle in this situation is in equilibrium.
(e)
The value of
Answer to Problem 6P
The value of
Explanation of Solution
Given info: The mass of the block is
The formula to calculate the spring force is,
Here,
The formula to calculate electric force is,
Here,
The net force is zero so it is expressed as,
Here,
Rearrange the above expression to find
Conclusion:
Therefore, the value of
(f)
To show: The coordinate
Answer to Problem 6P
Thus, the coordinate
Explanation of Solution
The mass of the block is
Given info:
From part (e), the value of
The formula to calculate the force equation is,
Here,
The formula to calculate the acceleration is,
Here,
The summation of the force is,
Here,
The new coordinate is,

Substitute
Substitute
This is the required equation of S.H.M.
Conclusion:
Therefore, the coordinate
(g)
The period of the simple harmonic motion.
Answer to Problem 6P
The period of the simple harmonic motion is
Explanation of Solution
Given info: The mass of the block is
From part (f), the equation for the S.H.M is,
The general equation of S.H.M is,
Here,
Compare the equation (4) and (5) as,
The formula to calculate the time period is,
Here,
Substitute
Conclusion:
Therefore, the period of the simple harmonic motion is
(h)
The time period depend on the electric field magnitude or not.
Answer to Problem 6P
The time period does not depend on the electric field magnitude.
Explanation of Solution
Given info: The mass of the block is
From part (g),the time period is,
In the above formula, there is no term that signifies electric field magnitude. So the time period is independent of electric field magnitude.
Conclusion:
Therefore, the time period does not depend on the electric field magnitude.
Want to see more full solutions like this?
Chapter 24 Solutions
Physics for Scientists and Engineers with Modern Physics
Additional Science Textbook Solutions
College Physics: A Strategic Approach (3rd Edition)
Microbiology Fundamentals: A Clinical Approach
Fundamentals Of Thermodynamics
MARINE BIOLOGY
Campbell Essential Biology (7th Edition)
Cosmic Perspective Fundamentals
- Help me make a visualize experimental setup using a word document. For the theory below.arrow_forwardHow to solve this, given answerarrow_forwardThree point-like charges are placed at the corners of a square as shown in the figure, 28.0 cm on each side. Find the minimum amount of work required by an external force to move the charge q1 to infinity. Let q1=-2.10 μC, q2=+2.40 μС, q3=+3.60 μC.arrow_forward
- A point charge of -4.00 nC is at the origin, and a second point charge of 6.00 nC is on the x axis at x= 0.820 mm . Find the magnitude and direction of the electric field at each of the following points on the x axis. x2 = 19.0 cmarrow_forwardFour point-like charges are placed as shown in the figure, three of them are at the corners and one at the center of a square, 36.0 cm on each side. What is the electric potential at the empty corner? Let q1=q3=+26.0 µС, q2=-28.0 μC, and q4=-48.0μc Varrow_forwardPLS HELparrow_forward
 Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
 Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning





