Glencoe Algebra 1, Student Edition, 9780079039897, 0079039898, 2018
18th Edition
ISBN: 9780079039897
Author: Carter
Publisher: McGraw Hill
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Question
Chapter 2.4, Problem 52PFA
(a)
To determine
Write an equation to show the perimeter of the square and the
(a)
Expert Solution
Answer to Problem 52PFA
Explanation of Solution
Given:
The figure of square with side
Condition given: both the figure have same perimeter.
Concept Used:
Square is having all 4 sides are equal and the Equilateral Triangle has 3 equal sides.
Perimeter of the square is 4 times its one side and the perimeter of an equilateral triangle is 3 times its one side.
Calculation:
Perimeter of Square =
Perimeter of Equilateral Triangle =
According to the condition both the perimeters are same.
Perimeter of Square = Perimeter of Equilateral Triangle
Equation:
Thus, the required equation is
(b)
To determine
Write all the steps with explanation while solving the equation.
(b)
Expert Solution
Answer to Problem 52PFA
Explanation of Solution
Given:
The figure of square with side
Condition given: both the figure have same perimeter.
Concept Used:
Square is having all 4 sides are equal and the Equilateral Triangle has 3 equal sides.
Perimeter of the square is 4 times its one side and the perimeter of an equilateral triangle is 3 times its one side.
Calculation:
Perimeter of Square =
Perimeter of Equilateral Triangle =
According to the condition both the perimeters are same.
Perimeter of Square = Perimeter of Equilateral Triangle
Equation:
Thus, the solution of the equation
(c)
To determine
Find the length of the side of the square.
(c)
Expert Solution
Answer to Problem 52PFA
Explanation of Solution
Given:
The figure of square with side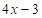 
and an equilateral triangle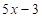 
Condition given: both the figure have same perimeter.
Concept Used:
Square is having all 4 sides are equal and the Equilateral Triangle has 3 equal sides.
Perimeter of the square is 4 times its one side and the perimeter of an equilateral triangle is 3 times its one side.
Calculation:
The side of the square:
Thus, the length of the side of the square is
(d)
To determine
Find the length of the side of the Triangle.
(d)
Expert Solution
Answer to Problem 52PFA
Explanation of Solution
Given:
The figure of square with side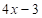 
and an equilateral triangle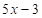 
Condition given: both the figure have same perimeter.
Concept Used:
Square is having all 4 sides are equal and the Equilateral Triangle has 3 equal sides.
Perimeter of the square is 4 times its one side and the perimeter of an equilateral triangle is 3 times its one side.
Calculation:
Length of the side of the Triangle:
Thus, the length of the side of the Triangle is
(e)
To determine
Find the area of the square.
(e)
Expert Solution
Answer to Problem 52PFA
Explanation of Solution
Given:
The figure of square with side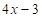 
and an equilateral triangle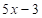 
Concept Used:
Square is having all 4 sides are equal
Area of the square is side times side:
Calculation:
The length of the side of the square is
Area of the square =
Thus, the area of the square is
Chapter 2 Solutions
Glencoe Algebra 1, Student Edition, 9780079039897, 0079039898, 2018
Ch. 2.1 - Prob. 1AGPCh. 2.1 - Prob. 1BGPCh. 2.1 - Prob. 2GPCh. 2.1 - Prob. 3GPCh. 2.1 - Prob. 4AGPCh. 2.1 - Prob. 4BGPCh. 2.1 - Prob. 5GPCh. 2.1 - Prob. 1CYUCh. 2.1 - Prob. 2CYUCh. 2.1 - Prob. 3CYU
Ch. 2.1 - Prob. 4CYUCh. 2.1 - Prob. 5CYUCh. 2.1 - Prob. 6CYUCh. 2.1 - Prob. 7CYUCh. 2.1 - Prob. 8CYUCh. 2.1 - Prob. 9CYUCh. 2.1 - Prob. 10CYUCh. 2.1 - Prob. 11CYUCh. 2.1 - Prob. 12CYUCh. 2.1 - Prob. 13CYUCh. 2.1 - Prob. 14CYUCh. 2.1 - Prob. 15CYUCh. 2.1 - Prob. 16CYUCh. 2.1 - Prob. 17CYUCh. 2.1 - Prob. 18CYUCh. 2.1 - Prob. 19CYUCh. 2.1 - Prob. 20CYUCh. 2.1 - Prob. 21PPSCh. 2.1 - Prob. 22PPSCh. 2.1 - Prob. 23PPSCh. 2.1 - Prob. 24PPSCh. 2.1 - Prob. 25PPSCh. 2.1 - Prob. 26PPSCh. 2.1 - Prob. 27PPSCh. 2.1 - Prob. 28PPSCh. 2.1 - Prob. 29PPSCh. 2.1 - Prob. 30PPSCh. 2.1 - Prob. 31PPSCh. 2.1 - Prob. 32PPSCh. 2.1 - Prob. 33PPSCh. 2.1 - Prob. 34PPSCh. 2.1 - Prob. 35PPSCh. 2.1 - Prob. 36PPSCh. 2.1 - Prob. 37PPSCh. 2.1 - Prob. 38PPSCh. 2.1 - Prob. 39PPSCh. 2.1 - Prob. 40PPSCh. 2.1 - Prob. 41PPSCh. 2.1 - Prob. 42PPSCh. 2.1 - Prob. 43PPSCh. 2.1 - Prob. 44PPSCh. 2.1 - Prob. 45PPSCh. 2.1 - Prob. 46PPSCh. 2.1 - Prob. 47HPCh. 2.1 - Prob. 48HPCh. 2.1 - Prob. 49HPCh. 2.1 - Prob. 50HPCh. 2.1 - Prob. 51PFACh. 2.1 - Prob. 52PFACh. 2.1 - Prob. 53PFACh. 2.1 - Prob. 54PFACh. 2.1 - Prob. 55PFACh. 2.1 - Prob. 56PFACh. 2.2 - Prob. 1AGPCh. 2.2 - Prob. 1BGPCh. 2.2 - Prob. 2AGPCh. 2.2 - Prob. 2BGPCh. 2.2 - Prob. 3AGPCh. 2.2 - Prob. 3BGPCh. 2.2 - Prob. 4GPCh. 2.2 - Prob. 1CYUCh. 2.2 - Prob. 2CYUCh. 2.2 - Prob. 3CYUCh. 2.2 - Prob. 4CYUCh. 2.2 - Prob. 5CYUCh. 2.2 - Prob. 6CYUCh. 2.2 - Prob. 7CYUCh. 2.2 - Prob. 8CYUCh. 2.2 - Prob. 9CYUCh. 2.2 - Prob. 10CYUCh. 2.2 - Prob. 11CYUCh. 2.2 - Prob. 12CYUCh. 2.2 - Prob. 13CYUCh. 2.2 - Prob. 14CYUCh. 2.2 - Prob. 15CYUCh. 2.2 - Prob. 16CYUCh. 2.2 - Prob. 17CYUCh. 2.2 - Prob. 18PPSCh. 2.2 - Prob. 19PPSCh. 2.2 - Prob. 20PPSCh. 2.2 - Prob. 21PPSCh. 2.2 - Prob. 22PPSCh. 2.2 - Prob. 23PPSCh. 2.2 - Prob. 24PPSCh. 2.2 - Prob. 25PPSCh. 2.2 - Prob. 26PPSCh. 2.2 - Prob. 27PPSCh. 2.2 - Prob. 28PPSCh. 2.2 - Prob. 29PPSCh. 2.2 - Prob. 30PPSCh. 2.2 - Prob. 31PPSCh. 2.2 - Prob. 32PPSCh. 2.2 - Prob. 33PPSCh. 2.2 - Prob. 34PPSCh. 2.2 - Prob. 35PPSCh. 2.2 - Prob. 36PPSCh. 2.2 - Prob. 37PPSCh. 2.2 - Prob. 38PPSCh. 2.2 - Prob. 39PPSCh. 2.2 - Prob. 40PPSCh. 2.2 - Prob. 41PPSCh. 2.2 - Prob. 42PPSCh. 2.2 - Prob. 43PPSCh. 2.2 - Prob. 44PPSCh. 2.2 - Prob. 45PPSCh. 2.2 - Prob. 46PPSCh. 2.2 - Prob. 47PPSCh. 2.2 - Prob. 48PPSCh. 2.2 - Prob. 49PPSCh. 2.2 - Prob. 50PPSCh. 2.2 - Prob. 51PPSCh. 2.2 - Prob. 52PPSCh. 2.2 - Prob. 53PPSCh. 2.2 - Prob. 54PPSCh. 2.2 - Prob. 55PPSCh. 2.2 - Prob. 56PPSCh. 2.2 - Prob. 57PPSCh. 2.2 - Prob. 58PPSCh. 2.2 - Prob. 59PPSCh. 2.2 - Prob. 60PPSCh. 2.2 - Prob. 61PPSCh. 2.2 - Prob. 62PPSCh. 2.2 - Prob. 63PPSCh. 2.2 - Prob. 64PPSCh. 2.2 - Prob. 65PPSCh. 2.2 - Prob. 66PPSCh. 2.2 - Prob. 67PPSCh. 2.2 - Prob. 68PPSCh. 2.2 - Prob. 69PPSCh. 2.2 - Prob. 70PPSCh. 2.2 - Prob. 71PPSCh. 2.2 - Prob. 72HPCh. 2.2 - Prob. 73HPCh. 2.2 - Prob. 74HPCh. 2.2 - Prob. 75HPCh. 2.2 - Prob. 76HPCh. 2.2 - Prob. 77HPCh. 2.2 - Prob. 78HPCh. 2.2 - Prob. 79PFACh. 2.2 - Prob. 80PFACh. 2.2 - Prob. 81PFACh. 2.2 - Prob. 82PFACh. 2.2 - Prob. 83PFACh. 2.3 - Prob. 1AGPCh. 2.3 - Prob. 1BGPCh. 2.3 - Prob. 2AGPCh. 2.3 - Prob. 2BGPCh. 2.3 - Prob. 3GPCh. 2.3 - Prob. 1CYUCh. 2.3 - Prob. 2CYUCh. 2.3 - Prob. 3CYUCh. 2.3 - Prob. 4CYUCh. 2.3 - Prob. 5CYUCh. 2.3 - Prob. 6CYUCh. 2.3 - Prob. 7CYUCh. 2.3 - Prob. 8CYUCh. 2.3 - Prob. 9CYUCh. 2.3 - Prob. 10CYUCh. 2.3 - Prob. 11PPSCh. 2.3 - Prob. 12PPSCh. 2.3 - Prob. 13PPSCh. 2.3 - Prob. 14PPSCh. 2.3 - Prob. 15PPSCh. 2.3 - Prob. 16PPSCh. 2.3 - Prob. 17PPSCh. 2.3 - Prob. 18PPSCh. 2.3 - Prob. 19PPSCh. 2.3 - Prob. 20PPSCh. 2.3 - Prob. 21PPSCh. 2.3 - Prob. 22PPSCh. 2.3 - Prob. 23PPSCh. 2.3 - Prob. 24PPSCh. 2.3 - Prob. 25PPSCh. 2.3 - Prob. 26PPSCh. 2.3 - Prob. 27PPSCh. 2.3 - Prob. 28PPSCh. 2.3 - Prob. 29PPSCh. 2.3 - Prob. 30PPSCh. 2.3 - Prob. 31PPSCh. 2.3 - Prob. 32PPSCh. 2.3 - Prob. 33PPSCh. 2.3 - Prob. 34PPSCh. 2.3 - Prob. 35PPSCh. 2.3 - Prob. 36PPSCh. 2.3 - Prob. 37PPSCh. 2.3 - Prob. 38PPSCh. 2.3 - Prob. 39PPSCh. 2.3 - Prob. 40PPSCh. 2.3 - Prob. 41PPSCh. 2.3 - Prob. 42PPSCh. 2.3 - Prob. 43PPSCh. 2.3 - Prob. 44PPSCh. 2.3 - Prob. 45PPSCh. 2.3 - Prob. 46PPSCh. 2.3 - Prob. 47PPSCh. 2.3 - Prob. 48PPSCh. 2.3 - Prob. 49PPSCh. 2.3 - Prob. 50PPSCh. 2.3 - Prob. 51PPSCh. 2.3 - Prob. 52PPSCh. 2.3 - Prob. 53HPCh. 2.3 - Prob. 54HPCh. 2.3 - Prob. 55HPCh. 2.3 - Prob. 56HPCh. 2.3 - Prob. 57HPCh. 2.3 - Prob. 58PFACh. 2.3 - Prob. 59PFACh. 2.3 - Prob. 60PFACh. 2.3 - Prob. 61PFACh. 2.3 - Prob. 62PFACh. 2.3 - Prob. 63PFACh. 2.3 - Prob. 64PFACh. 2.4 - Prob. 1AGPCh. 2.4 - Prob. 1BGPCh. 2.4 - Prob. 1CGPCh. 2.4 - Prob. 1DGPCh. 2.4 - Prob. 2AGPCh. 2.4 - Prob. 2BGPCh. 2.4 - Prob. 3AGPCh. 2.4 - Prob. 3BGPCh. 2.4 - Prob. 4GPCh. 2.4 - Prob. 1CYUCh. 2.4 - Prob. 2CYUCh. 2.4 - Prob. 3CYUCh. 2.4 - Prob. 4CYUCh. 2.4 - Prob. 5CYUCh. 2.4 - Prob. 6CYUCh. 2.4 - Prob. 7CYUCh. 2.4 - Prob. 8CYUCh. 2.4 - Prob. 9CYUCh. 2.4 - Prob. 10PPSCh. 2.4 - Prob. 11PPSCh. 2.4 - Prob. 12PPSCh. 2.4 - Prob. 13PPSCh. 2.4 - Prob. 14PPSCh. 2.4 - Prob. 15PPSCh. 2.4 - Prob. 16PPSCh. 2.4 - Prob. 17PPSCh. 2.4 - Prob. 18PPSCh. 2.4 - Prob. 19PPSCh. 2.4 - Prob. 20PPSCh. 2.4 - Prob. 21PPSCh. 2.4 - Prob. 22PPSCh. 2.4 - Prob. 23PPSCh. 2.4 - Prob. 24PPSCh. 2.4 - Prob. 25PPSCh. 2.4 - Prob. 26PPSCh. 2.4 - Prob. 27PPSCh. 2.4 - Prob. 28PPSCh. 2.4 - Prob. 29PPSCh. 2.4 - Prob. 30PPSCh. 2.4 - Prob. 31PPSCh. 2.4 - Prob. 32PPSCh. 2.4 - Prob. 33PPSCh. 2.4 - Prob. 34PPSCh. 2.4 - Prob. 35PPSCh. 2.4 - Prob. 36PPSCh. 2.4 - Prob. 37PPSCh. 2.4 - Prob. 38PPSCh. 2.4 - Prob. 39PPSCh. 2.4 - Prob. 40PPSCh. 2.4 - Prob. 41PPSCh. 2.4 - Prob. 42HPCh. 2.4 - Prob. 43HPCh. 2.4 - Prob. 44HPCh. 2.4 - Prob. 45HPCh. 2.4 - Prob. 46HPCh. 2.4 - Prob. 47HPCh. 2.4 - Prob. 48PFACh. 2.4 - Prob. 49PFACh. 2.4 - Prob. 50PFACh. 2.4 - Prob. 51PFACh. 2.4 - Prob. 52PFACh. 2.4 - Prob. 53PFACh. 2.4 - Prob. 54PFACh. 2.4 - Prob. 55PFACh. 2.4 - Prob. 56PFACh. 2.5 - Prob. 1GPCh. 2.5 - Prob. 2AGPCh. 2.5 - Prob. 2BGPCh. 2.5 - Prob. 3GPCh. 2.5 - Prob. 4GPCh. 2.5 - Prob. 1CYUCh. 2.5 - Prob. 2CYUCh. 2.5 - Prob. 3CYUCh. 2.5 - Prob. 4CYUCh. 2.5 - Prob. 5CYUCh. 2.5 - Prob. 6CYUCh. 2.5 - Prob. 7CYUCh. 2.5 - Prob. 8CYUCh. 2.5 - Prob. 9CYUCh. 2.5 - Prob. 10CYUCh. 2.5 - Prob. 11CYUCh. 2.5 - Prob. 12CYUCh. 2.5 - Prob. 13PPSCh. 2.5 - Prob. 14PPSCh. 2.5 - Prob. 15PPSCh. 2.5 - Prob. 16PPSCh. 2.5 - Prob. 17PPSCh. 2.5 - Prob. 18PPSCh. 2.5 - Prob. 19PPSCh. 2.5 - Prob. 20PPSCh. 2.5 - Prob. 21PPSCh. 2.5 - Prob. 22PPSCh. 2.5 - Prob. 23PPSCh. 2.5 - Prob. 24PPSCh. 2.5 - Prob. 25PPSCh. 2.5 - Prob. 26PPSCh. 2.5 - Prob. 27PPSCh. 2.5 - Prob. 28PPSCh. 2.5 - Prob. 29PPSCh. 2.5 - Prob. 30PPSCh. 2.5 - Prob. 31PPSCh. 2.5 - Prob. 32PPSCh. 2.5 - Prob. 33PPSCh. 2.5 - Prob. 34PPSCh. 2.5 - Prob. 35PPSCh. 2.5 - Prob. 36PPSCh. 2.5 - Prob. 37PPSCh. 2.5 - Prob. 38PPSCh. 2.5 - Prob. 39PPSCh. 2.5 - Prob. 40PPSCh. 2.5 - Prob. 41PPSCh. 2.5 - Prob. 42PPSCh. 2.5 - Prob. 43PPSCh. 2.5 - Prob. 44PPSCh. 2.5 - Prob. 45PPSCh. 2.5 - Prob. 46PPSCh. 2.5 - Prob. 47PPSCh. 2.5 - Prob. 48PPSCh. 2.5 - Prob. 49PPSCh. 2.5 - Prob. 50PPSCh. 2.5 - Prob. 51PPSCh. 2.5 - Prob. 52PPSCh. 2.5 - Prob. 53PPSCh. 2.5 - Prob. 54PPSCh. 2.5 - Prob. 55PPSCh. 2.5 - Prob. 56HPCh. 2.5 - Prob. 57HPCh. 2.5 - Prob. 58HPCh. 2.5 - Prob. 59HPCh. 2.5 - Prob. 60HPCh. 2.5 - Prob. 61HPCh. 2.5 - Prob. 62HPCh. 2.5 - Prob. 63HPCh. 2.5 - Prob. 64HPCh. 2.5 - Prob. 65PFACh. 2.5 - Prob. 66PFACh. 2.5 - Prob. 67PFACh. 2.5 - Prob. 68PFACh. 2.5 - Prob. 69PFACh. 2.5 - Prob. 70PFACh. 2.5 - Prob. 71PFACh. 2.5 - Prob. 72PFACh. 2.5 - Prob. 73PFACh. 2.5 - Prob. 74PFACh. 2.6 - Prob. 1AGPCh. 2.6 - Prob. 1BGPCh. 2.6 - Prob. 2AGPCh. 2.6 - Prob. 2BGPCh. 2.6 - Prob. 3AGPCh. 2.6 - Prob. 3BGPCh. 2.6 - Prob. 4GPCh. 2.6 - Prob. 5GPCh. 2.6 - Prob. 1CYUCh. 2.6 - Prob. 2CYUCh. 2.6 - Prob. 3CYUCh. 2.6 - Prob. 4CYUCh. 2.6 - Prob. 5CYUCh. 2.6 - Prob. 6CYUCh. 2.6 - Prob. 7CYUCh. 2.6 - Prob. 8CYUCh. 2.6 - Prob. 9PPSCh. 2.6 - Prob. 10PPSCh. 2.6 - Prob. 11PPSCh. 2.6 - Prob. 12PPSCh. 2.6 - Prob. 13PPSCh. 2.6 - Prob. 14PPSCh. 2.6 - Prob. 15PPSCh. 2.6 - Prob. 16PPSCh. 2.6 - Prob. 17PPSCh. 2.6 - Prob. 18PPSCh. 2.6 - Prob. 19PPSCh. 2.6 - Prob. 20PPSCh. 2.6 - Prob. 21PPSCh. 2.6 - Prob. 22PPSCh. 2.6 - Prob. 23PPSCh. 2.6 - Prob. 24PPSCh. 2.6 - Prob. 25PPSCh. 2.6 - Prob. 26PPSCh. 2.6 - Prob. 27PPSCh. 2.6 - Prob. 28PPSCh. 2.6 - Prob. 29PPSCh. 2.6 - Prob. 30PPSCh. 2.6 - Prob. 31PPSCh. 2.6 - Prob. 32PPSCh. 2.6 - Prob. 33PPSCh. 2.6 - Prob. 34PPSCh. 2.6 - Prob. 35PPSCh. 2.6 - Prob. 36PPSCh. 2.6 - Prob. 37PPSCh. 2.6 - Prob. 38PPSCh. 2.6 - Prob. 39PPSCh. 2.6 - Prob. 40PPSCh. 2.6 - Prob. 41PPSCh. 2.6 - Prob. 42PPSCh. 2.6 - Prob. 43PPSCh. 2.6 - Prob. 44PPSCh. 2.6 - Prob. 45PPSCh. 2.6 - Prob. 46HPCh. 2.6 - Prob. 47HPCh. 2.6 - Prob. 48HPCh. 2.6 - Prob. 49HPCh. 2.6 - Prob. 50HPCh. 2.6 - Prob. 51PFACh. 2.6 - Prob. 52PFACh. 2.6 - Prob. 53PFACh. 2.6 - Prob. 54PFACh. 2.6 - Prob. 55PFACh. 2.6 - Prob. 56PFACh. 2.6 - Prob. 57PFACh. 2.6 - Prob. 58PFACh. 2.6 - Prob. 59PFACh. 2.6 - Prob. 60PFACh. 2.7 - Prob. 1AGPCh. 2.7 - Prob. 1BGPCh. 2.7 - Prob. 1CGPCh. 2.7 - Prob. 1DGPCh. 2.7 - Prob. 2AGPCh. 2.7 - Prob. 2BGPCh. 2.7 - Prob. 3GPCh. 2.7 - Prob. 4GPCh. 2.7 - Prob. 1CYUCh. 2.7 - Prob. 2CYUCh. 2.7 - Prob. 3CYUCh. 2.7 - Prob. 4CYUCh. 2.7 - Prob. 5CYUCh. 2.7 - Prob. 6CYUCh. 2.7 - Prob. 7CYUCh. 2.7 - Prob. 8PPSCh. 2.7 - Prob. 9PPSCh. 2.7 - Prob. 10PPSCh. 2.7 - Prob. 11PPSCh. 2.7 - Prob. 12PPSCh. 2.7 - Prob. 13PPSCh. 2.7 - Prob. 14PPSCh. 2.7 - Prob. 15PPSCh. 2.7 - Prob. 16PPSCh. 2.7 - Prob. 17PPSCh. 2.7 - Prob. 18PPSCh. 2.7 - Prob. 19PPSCh. 2.7 - Prob. 20PPSCh. 2.7 - Prob. 21PPSCh. 2.7 - Prob. 22PPSCh. 2.7 - Prob. 23PPSCh. 2.7 - Prob. 24PPSCh. 2.7 - Prob. 25PPSCh. 2.7 - Prob. 26PPSCh. 2.7 - Prob. 27PPSCh. 2.7 - Prob. 28PPSCh. 2.7 - Prob. 29PPSCh. 2.7 - Prob. 30PPSCh. 2.7 - Prob. 31PPSCh. 2.7 - Prob. 32PPSCh. 2.7 - Prob. 33PPSCh. 2.7 - Prob. 34PPSCh. 2.7 - Prob. 35HPCh. 2.7 - Prob. 36HPCh. 2.7 - Prob. 37HPCh. 2.7 - Prob. 38HPCh. 2.7 - Prob. 39HPCh. 2.7 - Prob. 40HPCh. 2.7 - Prob. 41PFACh. 2.7 - Prob. 42PFACh. 2.7 - Prob. 43PFACh. 2.7 - Prob. 44PFACh. 2.7 - Prob. 45PFACh. 2.7 - Prob. 46PFACh. 2.7 - Prob. 47PFACh. 2.7 - Prob. 48PFACh. 2.7 - Prob. 49PFACh. 2 - Prob. 1SGRCh. 2 - Prob. 2SGRCh. 2 - Prob. 3SGRCh. 2 - Prob. 4SGRCh. 2 - Prob. 5SGRCh. 2 - Prob. 6SGRCh. 2 - Prob. 7SGRCh. 2 - Prob. 8SGRCh. 2 - Prob. 9SGRCh. 2 - Prob. 10SGRCh. 2 - Prob. 11SGRCh. 2 - Prob. 12SGRCh. 2 - Prob. 13SGRCh. 2 - Prob. 14SGRCh. 2 - Prob. 15SGRCh. 2 - Prob. 16SGRCh. 2 - Prob. 17SGRCh. 2 - Prob. 18SGRCh. 2 - Prob. 19SGRCh. 2 - Prob. 20SGRCh. 2 - Prob. 21SGRCh. 2 - Prob. 22SGRCh. 2 - Prob. 23SGRCh. 2 - Prob. 24SGRCh. 2 - Prob. 25SGRCh. 2 - Prob. 26SGRCh. 2 - Prob. 27SGRCh. 2 - Prob. 28SGRCh. 2 - Prob. 29SGRCh. 2 - Prob. 30SGRCh. 2 - Prob. 31SGRCh. 2 - Prob. 32SGRCh. 2 - Prob. 33SGRCh. 2 - Prob. 34SGRCh. 2 - Prob. 35SGRCh. 2 - Prob. 36SGRCh. 2 - Prob. 37SGRCh. 2 - Prob. 38SGRCh. 2 - Prob. 39SGRCh. 2 - Prob. 40SGRCh. 2 - Prob. 41SGRCh. 2 - Prob. 42SGRCh. 2 - Prob. 43SGRCh. 2 - Prob. 44SGRCh. 2 - Prob. 45SGRCh. 2 - Prob. 46SGRCh. 2 - Prob. 47SGRCh. 2 - Prob. 48SGRCh. 2 - Prob. 49SGRCh. 2 - Prob. 50SGRCh. 2 - Prob. 51SGRCh. 2 - Prob. 52SGRCh. 2 - Prob. 53SGRCh. 2 - Prob. 54SGRCh. 2 - Prob. 55SGRCh. 2 - Prob. 56SGRCh. 2 - Prob. 57SGRCh. 2 - Prob. 58SGRCh. 2 - Prob. 59SGRCh. 2 - Prob. 60SGRCh. 2 - Prob. 61SGRCh. 2 - Prob. 62SGRCh. 2 - Prob. 63SGRCh. 2 - Prob. 64SGRCh. 2 - Prob. 65SGRCh. 2 - Prob. 66SGRCh. 2 - Prob. 67SGRCh. 2 - Prob. 68SGRCh. 2 - Prob. 69SGRCh. 2 - Prob. 70SGRCh. 2 - Prob. 71SGRCh. 2 - Prob. 72SGRCh. 2 - Prob. 73SGRCh. 2 - Prob. 74SGRCh. 2 - Prob. 75SGRCh. 2 - Prob. 76SGRCh. 2 - Prob. 77SGRCh. 2 - Prob. 78SGRCh. 2 - Prob. 79SGRCh. 2 - Prob. 1PTCh. 2 - Prob. 2PTCh. 2 - Prob. 3PTCh. 2 - Prob. 4PTCh. 2 - Prob. 5PTCh. 2 - Prob. 6PTCh. 2 - Prob. 7PTCh. 2 - Prob. 8PTCh. 2 - Prob. 9PTCh. 2 - Prob. 10PTCh. 2 - Prob. 11PTCh. 2 - Prob. 12PTCh. 2 - Prob. 13PTCh. 2 - Prob. 14PTCh. 2 - Prob. 15PTCh. 2 - Prob. 16PTCh. 2 - Prob. 17PTCh. 2 - Prob. 18PTCh. 2 - Prob. 19PTCh. 2 - Prob. 20PTCh. 2 - Prob. 21PTCh. 2 - Prob. 22PTCh. 2 - Prob. 23PTCh. 2 - Prob. 24PTCh. 2 - Prob. 25PTCh. 2 - Prob. 1PFACh. 2 - Prob. 2PFACh. 2 - Prob. 3PFACh. 2 - Prob. 4PFACh. 2 - Prob. 5PFACh. 2 - Prob. 6PFACh. 2 - Prob. 7PFACh. 2 - Prob. 8PFACh. 2 - Prob. 9PFACh. 2 - Prob. 10PFACh. 2 - Prob. 11PFACh. 2 - Prob. 12PFACh. 2 - Prob. 13PFACh. 2 - Prob. 14PFACh. 2 - Prob. 15PFA
Additional Math Textbook Solutions
Find more solutions based on key concepts
Infinite limits at infinity Determine the following limits. 19. limx(3x129x7)
Calculus: Early Transcendentals (2nd Edition)
True or False? In Exercises 5–8, determine whether the statement is true or false. If it is false, rewrite it a...
Elementary Statistics: Picturing the World (7th Edition)
Mathematical Connections Explain why 25 cents is one-fourth of a dollar, yet 15 minutes is one-fourth of an hou...
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
The scale factor of the dilation and classify it as an enlargement or a reduction.
Pre-Algebra Student Edition
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, algebra and related others by exploring similar questions and additional content below.Similar questions
- (a) (b) (c) (d) de unique? Answer the following questions related to the linear system x + y + z = 2 x-y+z=0 2x + y 2 3 rewrite the linear system into the matrix-vector form A = 5 Fuse elementary row operation to solve this linear system. Is the solution use elementary row operation to find the inverse of A and then solve the linear system. Verify the solution is the same as (b). give the null space of matrix A and find the dimension of null space. give the column space of matrix A and find the dimension of the column space of A (Hint: use Rank-Nullity Theorem).arrow_forwardplease explain in a clear wayarrow_forwardSolve questions by Course Name Ordinary Differential Equationsarrow_forward
- Determine whether it's true or false and the reasoning is neededarrow_forward1. (20 pts) Determine whether the following statements are true (T) or false (F)? (A reasoning is required.) (1) Let V be the set of all ordered pairs of real numbers. Consider the following addition and scalar multiplication operations on u = u= (u1, u2) and v = (v1, v2): u + v = (U₁ + V₁, U₂ + v₂), ku = (ku₁, u₂). Is V a vector space under the above operations? U2 (2) The set Mmxn of all m×n matrices with the usual operations of addition and scalar multiplication is a vector space. α (3) The dimension of the vector space of all matrices A = [a b] in R2×2 with a+d=0 is 4. (4) The coordinate vector of p(x) = 2-x+x² in P3 relative to the basis S = {1, 1+x, x + x2} is [4 -2 1]. (5) If a 6×4 matrix A has a rank 3, then the dimension of N(A) is 3.arrow_forward5. (20%) The linear transformation L: P3 → P2 defined by L(f(x)) = f'(x)+ f(0). (a) Find the representing matrix A of L with respect to the ordered basis {x2, x, 1} for P3, and the ordered basis {2,1 - x} for P2. (b) Find the coordinates of the f(x) = 2x² +2 in P3 with respect to the ordered basis {x2,-x, 1}, and find the coordinates of L(f(x)) with respect to the ordered basis {2,1-x}arrow_forward
- For the spinner below, assume that the pointer can never lie on a borderline. Find the following probabilities. (enter the probabilities as fractions)arrow_forwardQuestions 1. Identify and describe potential bias in the study. 2. Identify and describe the way in which the selected participants may or may not represent the population as a whole. 3. Identify and describe the possible problems with the end results since the majority will be from females rather than an even split. 4. Identify and describe the possible problems with identifying females as possibly more vulnerable based on the data collected. 5. Identify a possible null hypothesis and problems in how the study might address this null hypothesis. 6. Identify one possible method of improving the study design and describe how it would improve the validity of the conclusions. 7. Identify a second possible method of improving the study design and describe how it would improve the validity of the conclusions.arrow_forwardThe Course Name Real Analysis please Solve questions by Real Analysisarrow_forward
- part 3 of the question is: A power outage occurs 6 min after the ride started. Passengers must wait for their cage to be manually cranked into the lowest position in order to exit the ride. Sine function model: where h is the height of the last passenger above the ground measured in feet and t is the time of operation of the ride in minutes. What is the height of the last passenger at the moment of the power outage? Verify your answer by evaluating the sine function model. Will the last passenger to board the ride need to wait in order to exit the ride? Explain.arrow_forward2. The duration of the ride is 15 min. (a) How many times does the last passenger who boarded the ride make a complete loop on the Ferris wheel? (b) What is the position of that passenger when the ride ends?arrow_forward3. A scientist recorded the movement of a pendulum for 10 s. The scientist began recording when the pendulum was at its resting position. The pendulum then moved right (positive displacement) and left (negative displacement) several times. The pendulum took 4 s to swing to the right and the left and then return to its resting position. The pendulum's furthest distance to either side was 6 in. Graph the function that represents the pendulum's displacement as a function of time. Answer: f(t) (a) Write an equation to represent the displacement of the pendulum as a function of time. (b) Graph the function. 10 9 8 7 6 5 4 3 2 1 0 t 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 -1 -5. -6 -7 -8 -9 -10-arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Algebra and Trigonometry (6th Edition)AlgebraISBN:9780134463216Author:Robert F. BlitzerPublisher:PEARSON
Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON
Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press
College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education
Algebra and Trigonometry (6th Edition)
Algebra
ISBN:9780134463216
Author:Robert F. Blitzer
Publisher:PEARSON
Contemporary Abstract Algebra
Algebra
ISBN:9781305657960
Author:Joseph Gallian
Publisher:Cengage Learning
Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning
Algebra And Trigonometry (11th Edition)
Algebra
ISBN:9780135163078
Author:Michael Sullivan
Publisher:PEARSON
Introduction to Linear Algebra, Fifth Edition
Algebra
ISBN:9780980232776
Author:Gilbert Strang
Publisher:Wellesley-Cambridge Press
College Algebra (Collegiate Math)
Algebra
ISBN:9780077836344
Author:Julie Miller, Donna Gerken
Publisher:McGraw-Hill Education
What is a Linear Equation in One Variable?; Author: Don't Memorise;https://www.youtube.com/watch?v=lDOYdBgtnjY;License: Standard YouTube License, CC-BY
Linear Equation | Solving Linear Equations | What is Linear Equation in one variable ?; Author: Najam Academy;https://www.youtube.com/watch?v=tHm3X_Ta_iE;License: Standard YouTube License, CC-BY