Chapter 24, Problem 42SP

Four equal-magnitude (4.0 $\mu \text{C}$) charges in vacuum are placed at the four corners of a square that is 20 cm on each side. Find the electric field at the center of the square (a) if the charges are all positive, (b) if the charges alternate in sign around the perimeter of the square, (c) if the charges have the following sequence around the square: plus, plus, minus, minus.

To determine

The electric field at the center of the square, iffour positively charged charges, having magnitude of each is $4\text{ μC}$, are placed at the four corners of the square.

Answer to Problem 42SP

Solution:

$\text{Zero}$

Explanation of Solution

Given data:

The length of each side of the square is $\text{20 cm}$.

The magnitude of each charge is $4\text{ μC}$.

Formula used:

Write the expression for the electric field

$E=\frac{kq}{r^2}$

Here, $E$ is the electric field, $k$ is the Coulomb’s constant, $q$ is the charge emitting the electric field and $r$ is the distance between the charge creating the electric field and the reference point.

Explanation:

In this case, all charges are of equal magnitude and polarity, and are located at the same distance from the center of the square.

Denote the charge by $q$ and the distance by $r$.

As all charges are positive, the direction of the electric field shall be outward and away from the charges, as shown in the figure below.

The electric field at the center of the square will the resultant electric filed due to all the electric fields acting on it. Therefore, the electric field at the center of the square will be the resultant of the electric fields due to charges at points A, B, C, and D.

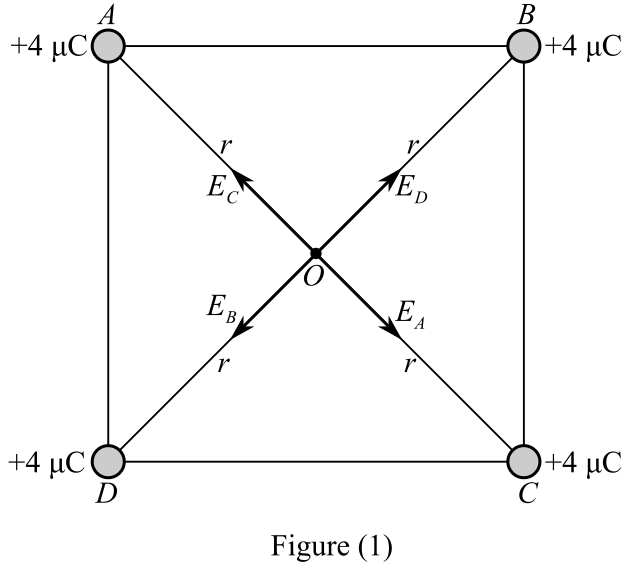
Recall the expression for the electric field.

$E=\frac{kq}{r^2}$

Refer to the above diagram and write the expression for the electric field at the corners of the square due to all the four-point charges that are placed at the corners of the square.

Write the expression for the electric field due to charges at the point A.

$E_A=\frac{kq}{r^2}$

Write the expression for the electric field due to charges at the point B.

$E_B=\frac{kq}{r^2}$

Write the expression for the electric field due to charges at the point C.

$E_C=\frac{kq}{r^2}$

Write the expression for the electric field due to charges at the point D.

$E_D=\frac{kq}{r^2}$

The resultant electric field at the center of the square will be

$E_{net}=\left(E_A-E_C\right)+\left(E_B-E_D\right)$

Substitute $\frac{kq}{r^2}$ for $E_A$, $\frac{kq}{r^2}$ for $E_C$, $\frac{kq}{r^2}$ for $E_B$, and $\frac{kq}{r^2}$ for $E_D$

$\begin{array}{c}{E}_{net}=\left(\frac{kq}{r^2}-\frac{kq}{r^2}\right)+\left(\frac{kq}{r^2}-\frac{kq}{r^2}\right)\\ \text{ = 0}\end{array}$

Conclusion:

The electric field at the center of the square if the charges are all positive is $\text{Zero}$.

To determine

The electric field at the center of the square if the charges alternate in sign around the perimeter of the square and the magnitude of each charge is $4\text{ μC}$.

Answer to Problem 42SP

Solution:

$\text{Zero}$

Explanation of Solution

Given data:

The length of each side of the square is $\text{20 cm}$.

The magnitude of each charge is $4\text{ μC}$.

Formula used:

Write the expression for the electric field

$E=\frac{kq}{r^2}$

Here, $E$ is the electric field, $k$ is the Coulomb’s constant, $q$ is the charge emitting the electric field and $r$ is the distance between the charge creating the electric field and the reference point.

Explanation:

In this case, all charges are of equal magnitude, however, they are placed such that they alternate in sign around the perimeter of the square. Also, they are located at the same distance from the center of the square.

Denote the charge by $q$ and the distance by $r$.

For positivecharges, the direction of the electric field shall be outward and away from the charges, while for negative charges the direction of the electric field shall be toward the charges as shown in the figure below.

The electric field at the center of the square will be the resultant electric filed due to all the electric fields acting on it. Therefore, the electric field at the center of the square will be the resultant of the electric fields due to charges at points A, B, C and D.

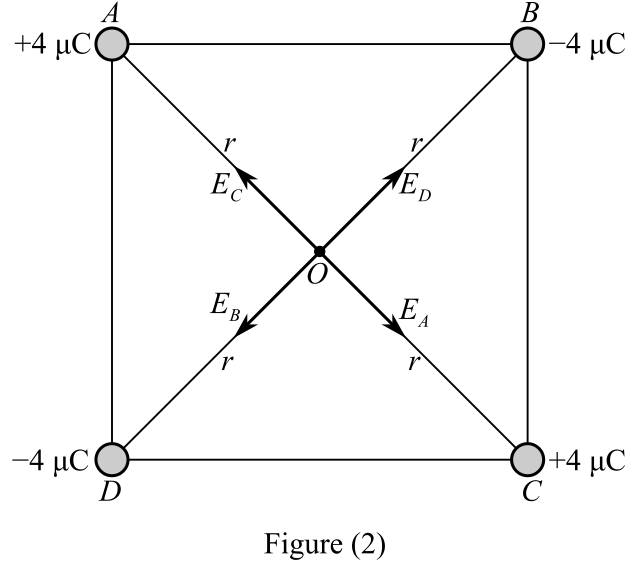
The expression for the electric field is given as

$E=\frac{kq}{r^2}$

Here, $E$ is the electric field, $k$ is the Coulomb’s constant, $q$ is the charge emitting the electric field and $r$ is the distance between the charge creating the electric field and the reference point.

Write the expression for the electric field due to charges at the point A.

$E_A=\frac{kq}{r^2}$

Write the expression for the electric field due to charges at the point B.

$E_B=\frac{-kq}{r^2}$

Write the expression for the electric field due to charges at the point C.

$E_C=\frac{kq}{r^2}$

Write the expression for the electric field due to charges at the point D.

$E_D=\frac{-kq}{r^2}$

The resultant electric field at the center of the square will be

$E_{net}=\left(E_A-E_C\right)+\left(E_B-E_D\right)$

Substitute $\frac{kq}{r^2}$ for $E_A$, $\frac{kq}{r^2}$ for $E_C$, $\frac{-kq}{r^2}$ for $E_B$ and $\frac{-kq}{r^2}$ for $E_D$.

$\begin{array}{c}{E}_{net}=\left(\frac{kq}{r^2}-\frac{kq}{r^2}\right)+\left[\frac{-kq}{r^2}-\left(\frac{-kq}{r^2}\right)\right]\\ \text{ = 0}\end{array}$

Conclusion:

The electric field at the center of the square, if the charges alternate in sign around the perimeter of the square, is $\text{Zero}$.

To determine

The electric field at the center of the square if the all the four charges, having magnitude of each as $4\text{ μC}$, follow the sequence plus, plus, minus, minus around the perimeter of the square.

Answer to Problem 42SP

Solution:

$\text{5}\text{.1 MN/C}$ toward the negative side.

Explanation of Solution

Given data:

The length of each side of the square is $\text{20 cm}$.

The magnitude of each charge is $4\text{ μC}$.

Formula used:

Write the expression for the electric field.

$E=\frac{kq}{r^2}$

Here, $E$ is the electric field, $k$ is the Coulomb’s constant, $q$ is the charge emitting the electric field, and $r$ is the distance between the charge creating the electric field and the reference point.

Write the expression for the relation between the length of the diagonal and side of a square

$d=l\sqrt{2}$

Here, $d$ is the length of the diagonal and $l$ is the length of each side of the square.

Write the expression for the net (resultant) electric field

$E_{net}=\sqrt{E_1^2+E_2^2+2E_1{E}_2\cos \theta }$

Here, $E_{net}$ is the net (resultant) electric field, $E_1$ is the electric field due to charge 1, $E_2$ is the electric field due to charge 2 and $\theta$ is the angle between the two electric field $E_1$ and $E_2$.

Explanation:

In this case, all charges are of equal magnitude, however, they are placed such the charges on the top are positive while the charges on the bottom are negative. Also, they are located at the same distance from the center of the square.

Denote the charge by $q$ and the distance by $r$.

For positive charges, the direction of the electric field shall be outward and away from the charges, while for negative charges the direction of the electric field shall be toward the charges, as shown in the figure below.

The electric field at the center of the square will be the resultant electric filed due to all the electric fields acting on it. Therefore, the electric field at the center of the sphere will be the resultant of the electric fields due to charges at points A, B, C and D.

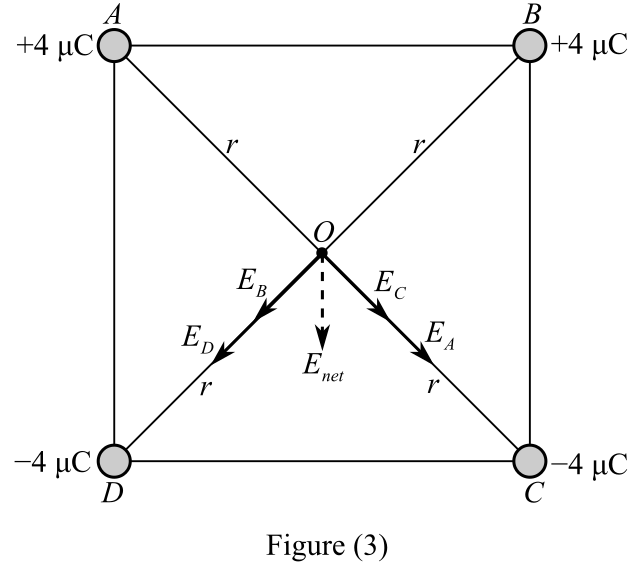
Recall the expression for diagonal length of a square.

$d=l\sqrt{2}$

Here, $d$ is the length of the diagonal and $l$ is the length of each side of the square.

Apply the equation mentioned above to determine the distance $r$, which is half the length of the diagonal.

Write the expression for distance $r$.

$r=\frac{1}{2}\left(l\sqrt{2}\right)$

Substitute $20\text{ cm}$ for $l$.

$\begin{array}{c}r=\frac{1}{2}\left(20\text{ cm}\sqrt{2}\right)\\ =\frac{1}{2}\left(20\text{ cm}\left(\frac{{10}^{-2}\text{ m}}{1\text{ cm}}\right)\sqrt{2}\right)\\ =\frac{1}{2}\left(0.2\sqrt{2}\right)\\ =\text{0}\text{.141 m}\end{array}$

Write the expression for the electric field.

$E=\frac{kq}{r^2}$

Here, $E$ is the electric field, $k$ is the Coulomb’s constant, $q$ is the charge emitting the electric field and $r$ is the distance from the charge creating the electric field and the reference point.

Refer to the above diagram and write the expression for the electric field due to charges at A, B, C and D.

Write the expression for the electric field due to charges at the point A.

$E_A=\frac{kq}{r^2}$

Write the expression for the electric field due to charges at the point B.

$E_B=-\frac{kq}{r^2}$

Write the expression for the electric field due to charges at the point C.

$E_C=\frac{kq}{r^2}$

Write the expression for the electric field due to charges at the point D.

$E_D=\frac{-kq}{r^2}$

Recall the expression for the resultant electric field at the center of the square.

$E_{net}=\sqrt{E_1^2+E_2^2+2E_1{E}_2\cos \theta }$

The angle between sum of electric field due to C and A, and D and B is $90°$.

Substitute $90°$ for $\theta$.

$\begin{array}{c}{E}_{net}=\sqrt{E_1^2+E_2^2+2E_1{E}_2\cos \left(90°\right)}\\ =\sqrt{E_1^2+E_2^2}\end{array}$

Understand that $E_1$ is the sum of electric field due to C and A, and $E_2$ is the sum of electric field due to C and A. Therefore, the expression is written as,

$\begin{array}{c}{E}_{net}=\sqrt{{\left(E_A+E_C\right)}^2+{\left(E_B+E_D\right)}^2}\\ =\sqrt{{\left(\frac{kq}{r^2}+\frac{kq}{r^2}\right)}^2+{\left(\frac{-kq}{r^2}+\frac{-kq}{r^2}\right)}^2}\\ =\sqrt{4{\left(\frac{kq}{r^2}\right)}^2+4{\left(\frac{kq}{r^2}\right)}^2}\\ =\text{2}\sqrt{2}\left(\frac{kq}{r^2}\right)\end{array}$

Substitute $9\times {10}^9{\text{ Nm}}^{\text{2}}{\text{/C}}^{\text{2}}$ for $k$, $4\text{ μC}$ $4\times {10}^{-6}\text{ C}$ for $q$ and $\text{0}\text{.141 m}$ for $r$

$\begin{array}{c}{E}_{net}=2\sqrt{2}\left(\frac{\left(9\times {10}^9\right)\left(4\text{ μC}\right)}{{(0.141)}^2}\right)\\ =2\sqrt{2}\left(\frac{\left(9\times {10}^9\right)\left(4\text{ μC}\left(\frac{{10}^{-6}\text{ C}}{1\text{ μC}}\right)\right)}{{\left(0.141\right)}^2}\right)\\ =\text{5}\text{.12}\times {10}^6\text{ N/C}\\ =\text{5}\text{.1 MN/C}\end{array}$.

Conclusion:

The electric field at the center of the square if the charges follow the sequence plus, plus, minus, minus around the perimeter of the square is $\text{5}\text{.1 MN/C}$.