Finite Mathematics and Applied Calculus (MindTap Course List)
7th Edition
ISBN: 9781337274203
Author: Stefan Waner, Steven Costenoble
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 2.4, Problem 25E
Internet Use The following graph shows the percentage of U.S. households using the Internet at home in 2010 as a function of household income (the data points) and a logistic model of these data (the curve).49
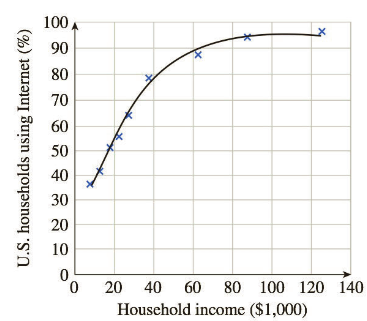
The logistic model is
a. According to the model, what percentage of extremely wealthy households used the Internet?
b. For low incomes the logistic model is approximately exponential. Which exponential model best approximates
c. According to the model, 50% of households of what income used the Internet in 2010? (Round the answer to the nearest $1,000.)
Expert Solution & Answer
Trending nowThis is a popular solution!
Students have asked these similar questions
Show that the Laplace equation in Cartesian coordinates:
J²u
J²u
+
= 0
მx2 Jy2
can be reduced to the following form in cylindrical polar coordinates:
湯(
ди
1 8²u
+
Or 7,2 მ)2
= 0.
Find integrating factor
Draw the vertical and horizontal asymptotes. Then plot the intercepts (if any), and plot at least one point on each side of each vertical asymptote.
Chapter 2 Solutions
Finite Mathematics and Applied Calculus (MindTap Course List)
Ch. 2.1 - In Exercises 16, (a) state the values of a, b, and...Ch. 2.1 - In Exercises 16, (a) state the values of a, b, and...Ch. 2.1 - In Exercises 16, (a) state the values of a, b, and...Ch. 2.1 - In Exercises 16, (a) state the values of a, b, and...Ch. 2.1 - In Exercises 16, (a) state the values of a, b, and...Ch. 2.1 - Prob. 6ECh. 2.1 - Prob. 7ECh. 2.1 - Prob. 8ECh. 2.1 - In Exercises 716, sketch the graph of the...Ch. 2.1 - Prob. 10E
Ch. 2.1 - Prob. 11ECh. 2.1 - In Exercises 716, sketch the graph of the...Ch. 2.1 - In Exercises 716, sketch the graph of the...Ch. 2.1 - Prob. 14ECh. 2.1 - Prob. 15ECh. 2.1 - Prob. 16ECh. 2.1 - In Exercises 1720, for each demand equation,...Ch. 2.1 - Prob. 18ECh. 2.1 - Prob. 19ECh. 2.1 - Prob. 20ECh. 2.1 - Prob. 21ECh. 2.1 - In Exercises 2124, use technology to find the...Ch. 2.1 - Prob. 23ECh. 2.1 - In Exercises 2124, use technology to find the...Ch. 2.1 - World Military Expenditure The following chart...Ch. 2.1 - Education Expenditure The following chart shows...Ch. 2.1 - Oil Imports from Mexico Crude oil imports to the...Ch. 2.1 - Oil Production in Mexico Crude oil production by...Ch. 2.1 - GE Net Income 20092013 The annual net income of...Ch. 2.1 - GE Net Income 20072011 The annual net income of...Ch. 2.1 - Revenue The market research department of the...Ch. 2.1 - Prob. 32ECh. 2.1 - Revenue Pack-Em-In Real Estate is building a new...Ch. 2.1 - Revenue Pack-Em-In has another development in the...Ch. 2.1 - Revenue from Monorail Service, Las Vegas In 2005...Ch. 2.1 - Revenue from Monorail Service, Mars The Utarek...Ch. 2.1 - Website Profit You operate a gaming website,...Ch. 2.1 - T-Shirt Profit Two fraternities, Sig Ep and Ep...Ch. 2.1 - Website Profit The latest demand equation for your...Ch. 2.1 - T-Shirt Profit The latest demand equation for your...Ch. 2.1 - Nightclub Management You have just opened a new...Ch. 2.1 - Television Advertising As sales manager for...Ch. 2.1 - Prob. 43ECh. 2.1 - Prob. 44ECh. 2.1 - iPod Sales The following table shows Apple iPod...Ch. 2.1 - iPod Sales The following table shows Apple iPod...Ch. 2.1 - What can you say about the graph of f(x)=ax2+bx+c...Ch. 2.1 - Prob. 48ECh. 2.1 - Multiple choice: Following is the graph of...Ch. 2.1 - Prob. 50ECh. 2.1 - Prob. 51ECh. 2.1 - Prob. 52ECh. 2.1 - Prob. 53ECh. 2.1 - Prob. 54ECh. 2.1 - Prob. 55ECh. 2.1 - Prob. 56ECh. 2.1 - Prob. 57ECh. 2.1 - Prob. 58ECh. 2.1 - Prob. 59ECh. 2.1 - Prob. 60ECh. 2.1 - If the revenue function for a particular commodity...Ch. 2.1 - If the revenue function for a particular commodity...Ch. 2.2 - In Exercises 1-12, compute the missing values in...Ch. 2.2 - In Exercises 1-12, compute the missing values in...Ch. 2.2 - In Exercises 1-12, compute the missing values in...Ch. 2.2 - Prob. 4ECh. 2.2 - Prob. 5ECh. 2.2 - In Exercises 1-12, compute the missing values in...Ch. 2.2 - Prob. 7ECh. 2.2 - Prob. 8ECh. 2.2 - Prob. 9ECh. 2.2 - Prob. 10ECh. 2.2 - In Exercises 1-12, compute the missing values in...Ch. 2.2 - Prob. 12ECh. 2.2 - In Exercises 13-18, graph the given function using...Ch. 2.2 - Prob. 14ECh. 2.2 - Prob. 15ECh. 2.2 - In Exercises 13-18, graph the given function using...Ch. 2.2 - Prob. 17ECh. 2.2 - In Exercises 13-18, graph the given function using...Ch. 2.2 - In Exercises 19-24 the values of two functions, f...Ch. 2.2 - Prob. 20ECh. 2.2 - Prob. 21ECh. 2.2 - Prob. 22ECh. 2.2 - Prob. 23ECh. 2.2 - Prob. 24ECh. 2.2 - In Exercises 25-30, supply a valid technology...Ch. 2.2 - Prob. 26ECh. 2.2 - Prob. 27ECh. 2.2 - Prob. 28ECh. 2.2 - In Exercises 25-30, supply a valid technology...Ch. 2.2 - In Exercises 25-30, supply a valid technology...Ch. 2.2 - Prob. 31ECh. 2.2 - Prob. 32ECh. 2.2 - Prob. 33ECh. 2.2 - Prob. 34ECh. 2.2 - Prob. 35ECh. 2.2 - Prob. 36ECh. 2.2 - Prob. 37ECh. 2.2 - Prob. 38ECh. 2.2 - Prob. 39ECh. 2.2 - Prob. 40ECh. 2.2 - Prob. 41ECh. 2.2 - Prob. 42ECh. 2.2 - Prob. 43ECh. 2.2 - Prob. 44ECh. 2.2 - Prob. 45ECh. 2.2 - Prob. 46ECh. 2.2 - In Exercises 47-54, model the data using an...Ch. 2.2 - Prob. 48ECh. 2.2 - Prob. 49ECh. 2.2 - Prob. 50ECh. 2.2 - In Exercises 47-54, model the data using an...Ch. 2.2 - Prob. 52ECh. 2.2 - In Exercises 47-54, model the data using an...Ch. 2.2 - Prob. 54ECh. 2.2 - Prob. 55ECh. 2.2 - Prob. 56ECh. 2.2 - In Exercises 55-62, find an equation for an...Ch. 2.2 - Prob. 58ECh. 2.2 - In Exercises 55-62, find an equation for an...Ch. 2.2 - In Exercises 55-62, find an equation for an...Ch. 2.2 - Prob. 61ECh. 2.2 - Prob. 62ECh. 2.2 - In Exercises 63-66, obtain an exponential function...Ch. 2.2 - Prob. 64ECh. 2.2 - In Exercises 63-66, obtain an exponential function...Ch. 2.2 - Prob. 66ECh. 2.2 - Prob. 67ECh. 2.2 - Prob. 68ECh. 2.2 - In Exercises 67-70, use technology to find the...Ch. 2.2 - Prob. 70ECh. 2.2 - Aspirin Soon after taking an aspirin, a patient...Ch. 2.2 - Alcohol After a large number of drinks, a person...Ch. 2.2 - Prob. 73ECh. 2.2 - Revenue The annual revenue of Amazon rose from...Ch. 2.2 - Prob. 75ECh. 2.2 - Prob. 76ECh. 2.2 - Prob. 77ECh. 2.2 - Prob. 78ECh. 2.2 - Bacteria A bacteria culture starts with 1,000...Ch. 2.2 - Prob. 80ECh. 2.2 - Prob. 81ECh. 2.2 - The 2003 SARS Outbreak A few weeks into the deadly...Ch. 2.2 - The 2014 Ebola Outbreak In the first six months of...Ch. 2.2 - Prob. 84ECh. 2.2 - Investments In August 2013, E*TRADE Financial was...Ch. 2.2 - Investments In August 2013, Ally Bank was offering...Ch. 2.2 - Prob. 87ECh. 2.2 - Prob. 88ECh. 2.2 - Investments Rock Solid Bank Trust is offering a...Ch. 2.2 - Savings FlybynightSavings.com is offering a...Ch. 2.2 - Prob. 91ECh. 2.2 - Home Prices The median selling price of an...Ch. 2.2 - Climate Change The most abundant greenhouse gas is...Ch. 2.2 - Prob. 94ECh. 2.2 - New York City Housing Costs: Downtown The...Ch. 2.2 - New York City Housing Costs: Uptown The following...Ch. 2.2 - Facebook The following table gives the approximate...Ch. 2.2 - Prob. 98ECh. 2.2 - Prob. 99ECh. 2.2 - Prob. 100ECh. 2.2 - Prob. 101ECh. 2.2 - Prob. 102ECh. 2.2 - Prob. 103ECh. 2.2 - Prob. 104ECh. 2.2 - Prob. 105ECh. 2.2 - Describe a real-life situation in which a...Ch. 2.2 - Prob. 107ECh. 2.2 - Prob. 108ECh. 2.2 - Prob. 109ECh. 2.2 - Prob. 110ECh. 2.3 - If y=4x, then x=.Ch. 2.3 - If y=log6x, then x=.Ch. 2.3 - Simplify: 2log28.Ch. 2.3 - Prob. 4ECh. 2.3 - Simplify: ln(ex).Ch. 2.3 - Simplify: lna.Ch. 2.3 - In Exercises 7-14, graph the given function....Ch. 2.3 - Prob. 8ECh. 2.3 - In Exercises 7-14, graph the given function....Ch. 2.3 - Prob. 10ECh. 2.3 - In Exercises 7-14, graph the given function....Ch. 2.3 - Prob. 12ECh. 2.3 - Prob. 13ECh. 2.3 - Prob. 14ECh. 2.3 - In Exercises 15-20, find the associated...Ch. 2.3 - Prob. 16ECh. 2.3 - Prob. 17ECh. 2.3 - Prob. 18ECh. 2.3 - In Exercises 15-20, find the associated...Ch. 2.3 - Prob. 20ECh. 2.3 - In Exercises 21-26, find the associated half-life...Ch. 2.3 - Prob. 22ECh. 2.3 - Prob. 23ECh. 2.3 - Prob. 24ECh. 2.3 - In Exercises 21-26, find the associated half-life...Ch. 2.3 - Prob. 26ECh. 2.3 - In Exercises 27-32, convert the given exponential...Ch. 2.3 - Prob. 28ECh. 2.3 - In Exercises 27-32, convert the given exponential...Ch. 2.3 - Prob. 30ECh. 2.3 - In Exercises 27-32, convert the given exponential...Ch. 2.3 - Prob. 32ECh. 2.3 - Investments How long will it take a $500...Ch. 2.3 - Prob. 34ECh. 2.3 - Investments How long, to the nearest year, will it...Ch. 2.3 - Investments How long, to the nearest year, will it...Ch. 2.3 - Prob. 37ECh. 2.3 - Depreciation My investment in OHaganBooks.com...Ch. 2.3 - Carbon Dating The amount of carbon 14 remaining in...Ch. 2.3 - Carbon Dating Refer to Exercise 39. How old, to...Ch. 2.3 - Long-Term Investments Exercises 41-48 are based on...Ch. 2.3 - Long-Term Investments Exercises 41-48 are based on...Ch. 2.3 - Long-Term Investments Exercises 41-48 are based on...Ch. 2.3 - Long-Term Investments Exercises 41-48 are based on...Ch. 2.3 - Long-Term Investments Exercises 41-48 are based on...Ch. 2.3 - Long-Term Investments Exercises 41-48 are based on...Ch. 2.3 - Prob. 47ECh. 2.3 - Prob. 48ECh. 2.3 - Half-Life The amount of radium 226 remaining in a...Ch. 2.3 - Half-Life The amount of iodine 131 remaining in a...Ch. 2.3 - Automobiles The rate of auto thefts triples every...Ch. 2.3 - Televisions The rate of television thefts is...Ch. 2.3 - Half-Life The half-life of cobalt 60 is 5 years....Ch. 2.3 - Half-Life The half-life of strontium 90 is 28...Ch. 2.3 - Prob. 55ECh. 2.3 - Prob. 56ECh. 2.3 - Aspirin Soon after taking an aspirin, a patient...Ch. 2.3 - Alcohol After a large number of drinks, a person...Ch. 2.3 - Prob. 59ECh. 2.3 - Prob. 60ECh. 2.3 - Prob. 61ECh. 2.3 - Prob. 62ECh. 2.3 - Prob. 63ECh. 2.3 - Prob. 64ECh. 2.3 - Richter Scale The Richter scale is used to measure...Ch. 2.3 - Sound Intensity The loudness of a sound is...Ch. 2.3 - Prob. 67ECh. 2.3 - Prob. 68ECh. 2.3 - On the same set of axes, graph y=lnx, y=Alnx, and...Ch. 2.3 - Prob. 70ECh. 2.3 - Prob. 71ECh. 2.3 - Of what use are logarithms, now that they are no...Ch. 2.3 - Prob. 73ECh. 2.3 - Prob. 74ECh. 2.3 - Prob. 75ECh. 2.3 - Prob. 76ECh. 2.3 - Prob. 77ECh. 2.4 - In Exercises 1-6, find N, A, and b; give a...Ch. 2.4 - Prob. 2ECh. 2.4 - Prob. 3ECh. 2.4 - Prob. 4ECh. 2.4 - Prob. 5ECh. 2.4 - Prob. 6ECh. 2.4 - Prob. 7ECh. 2.4 - Prob. 8ECh. 2.4 - Prob. 9ECh. 2.4 - Prob. 10ECh. 2.4 - Prob. 11ECh. 2.4 - Prob. 12ECh. 2.4 - Prob. 13ECh. 2.4 - Prob. 14ECh. 2.4 - Prob. 15ECh. 2.4 - Prob. 16ECh. 2.4 - Prob. 17ECh. 2.4 - In Exercises 17-20, use technology to find a...Ch. 2.4 - Prob. 19ECh. 2.4 - Prob. 20ECh. 2.4 - Prob. 21ECh. 2.4 - Prob. 22ECh. 2.4 - Prob. 23ECh. 2.4 - Prob. 24ECh. 2.4 - Internet Use The following graph shows the...Ch. 2.4 - Internet Use The following graph shows the...Ch. 2.4 - Prob. 27ECh. 2.4 - Epidemics Last year's epidemic of Martian flu...Ch. 2.4 - Sales You have sold 100 I Calculus T-shirts, and...Ch. 2.4 - Prob. 30ECh. 2.4 - Prob. 31ECh. 2.4 - Prob. 33ECh. 2.4 - College Basketball: Women The following table...Ch. 2.4 - Prob. 35ECh. 2.4 - Exercises 35 and 36 are based on the discussion...Ch. 2.4 - Prob. 37ECh. 2.4 - Prob. 38ECh. 2.4 - Prob. 39ECh. 2.4 - Prob. 40ECh. 2.4 - Prob. 41ECh. 2.4 - Prob. 42ECh. 2.4 - Prob. 43ECh. 2.4 - Prob. 44ECh. 2 - Sketch the graph of the quadratic functions in...Ch. 2 - Prob. 2RECh. 2 - Prob. 3RECh. 2 - Prob. 4RECh. 2 - Prob. 5RECh. 2 - Prob. 6RECh. 2 - Prob. 7RECh. 2 - Prob. 8RECh. 2 - Prob. 9RECh. 2 - Prob. 10RECh. 2 - Prob. 11RECh. 2 - Prob. 12RECh. 2 - Prob. 13RECh. 2 - Prob. 14RECh. 2 - In Exercises 15-18, find a formula of the form...Ch. 2 - Prob. 16RECh. 2 - Prob. 17RECh. 2 - Prob. 18RECh. 2 - Prob. 19RECh. 2 - Prob. 20RECh. 2 - In Exercises 21-24, use the given information to...Ch. 2 - In Exercises 21-24, use the given information to...Ch. 2 - Prob. 23RECh. 2 - Prob. 24RECh. 2 - Prob. 25RECh. 2 - In Exercises 25-28, find the time required, to the...Ch. 2 - In Exercises 25-28, find the time required, to the...Ch. 2 - In Exercises 25-28, find the time required, to the...Ch. 2 - In Exercises 29-32, find an equation for the...Ch. 2 - In Exercises 29-32, find an equation for the...Ch. 2 - In Exercises 29-32, find an equation for the...Ch. 2 - In Exercises 29-32, find an equation for the...Ch. 2 - Website Traffic The daily traffic (hits per day)...Ch. 2 - Revenue and Profit Some time ago, a consultant...Ch. 2 - Revenue and Profit Billy-Sean OHagan is John...Ch. 2 - Lobsters Marjory Duffin, CEO of Duffin House, is...Ch. 2 - Stock Prices In the period immediately following...Ch. 2 - Prob. 39RECh. 2 - Prob. 40RECh. 2 - Prob. 41RECh. 2 - Prob. 42RECh. 2 - Prob. 43RECh. 2 - Prob. 44RECh. 2 - Prob. 45RECh. 2 - Prob. 50RE
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- Draw the asymptotes (if there are any). Then plot two points on each piece of the graph.arrow_forwardCancel Done RESET Suppose that R(x) is a polynomial of degree 7 whose coefficients are real numbers. Also, suppose that R(x) has the following zeros. -1-4i, -3i, 5+i Answer the following. (a) Find another zero of R(x). ☐ | | | | |│ | | | -1 བ ¢ Live Adjust Filters Croparrow_forwardSuppose that R (x) is a polynomial of degree 7 whose coefficients are real numbers. Also, suppose that R (x) has the following zeros. -1-4i, -3i, 5+i Answer the following. (c) What is the maximum number of nonreal zeros that R (x) can have? ☐arrow_forward
- Suppose that R (x) is a polynomial of degree 7 whose coefficients are real numbers. Also, suppose that R (x) has the following zeros. -1-4i, -3i, 5+i Answer the following. (b) What is the maximum number of real zeros that R (x) can have? ☐arrow_forwardi need help please dont use chat gptarrow_forward3.1 Limits 1. If lim f(x)=-6 and lim f(x)=5, then lim f(x). Explain your choice. x+3° x+3* x+3 (a) Is 5 (c) Does not exist (b) is 6 (d) is infinitearrow_forward
- 1 pts Let F and G be vector fields such that ▼ × F(0, 0, 0) = (0.76, -9.78, 3.29), G(0, 0, 0) = (−3.99, 6.15, 2.94), and G is irrotational. Then sin(5V (F × G)) at (0, 0, 0) is Question 1 -0.246 0.072 -0.934 0.478 -0.914 -0.855 0.710 0.262 .arrow_forward2. Answer the following questions. (A) [50%] Given the vector field F(x, y, z) = (x²y, e", yz²), verify the differential identity Vx (VF) V(V •F) - V²F (B) [50%] Remark. You are confined to use the differential identities. Let u and v be scalar fields, and F be a vector field given by F = (Vu) x (Vv) (i) Show that F is solenoidal (or incompressible). (ii) Show that G = (uvv – vVu) is a vector potential for F.arrow_forwardA driver is traveling along a straight road when a buffalo runs into the street. This driver has a reaction time of 0.75 seconds. When the driver sees the buffalo he is traveling at 44 ft/s, his car can decelerate at 2 ft/s^2 when the brakes are applied. What is the stopping distance between when the driver first saw the buffalo, to when the car stops.arrow_forward
- Topic 2 Evaluate S x dx, using u-substitution. Then find the integral using 1-x2 trigonometric substitution. Discuss the results! Topic 3 Explain what an elementary anti-derivative is. Then consider the following ex integrals: fed dx x 1 Sdx In x Joseph Liouville proved that the first integral does not have an elementary anti- derivative Use this fact to prove that the second integral does not have an elementary anti-derivative. (hint: use an appropriate u-substitution!)arrow_forward1. Given the vector field F(x, y, z) = -xi, verify the relation 1 V.F(0,0,0) = lim 0+ volume inside Se ff F• Nds SE where SE is the surface enclosing a cube centred at the origin and having edges of length 2€. Then, determine if the origin is sink or source.arrow_forward4 3 2 -5 4-3 -2 -1 1 2 3 4 5 12 23 -4 The function graphed above is: Increasing on the interval(s) Decreasing on the interval(s)arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Functions and Change: A Modeling Approach to Coll...AlgebraISBN:9781337111348Author:Bruce Crauder, Benny Evans, Alan NoellPublisher:Cengage Learning
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Functions and Change: A Modeling Approach to Coll...
Algebra
ISBN:9781337111348
Author:Bruce Crauder, Benny Evans, Alan Noell
Publisher:Cengage Learning
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
College Algebra
Algebra
ISBN:9781305115545
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill
Algebra and Trigonometry (MindTap Course List)
Algebra
ISBN:9781305071742
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
01 - What Is A Differential Equation in Calculus? Learn to Solve Ordinary Differential Equations.; Author: Math and Science;https://www.youtube.com/watch?v=K80YEHQpx9g;License: Standard YouTube License, CC-BY
Higher Order Differential Equation with constant coefficient (GATE) (Part 1) l GATE 2018; Author: GATE Lectures by Dishank;https://www.youtube.com/watch?v=ODxP7BbqAjA;License: Standard YouTube License, CC-BY
Solution of Differential Equations and Initial Value Problems; Author: Jefril Amboy;https://www.youtube.com/watch?v=Q68sk7XS-dc;License: Standard YouTube License, CC-BY