Physics for Scientists and Engineers
10th Edition
ISBN: 9781337553278
Author: Raymond A. Serway, John W. Jewett
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 23, Problem 23P
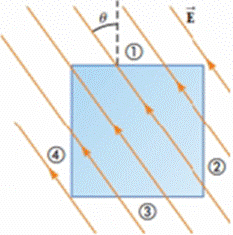
Figure P23.23 represents the top view of a cubic gaussian surface in a uniform electric field
Figure P23.23
Expert Solution & Answer
Trending nowThis is a popular solution!
Students have asked these similar questions
A Gaussian surface in the form of a hemisphere of radius R = 5.68 cm lies in a uniform electric field of magnitude E = 2.50 N/C. The surface encloses no net charge. At the (flat) base of the surface, the field is perpendicular to the surface and directed into the surface.What is the flux through (a) the base and (b) the curved portion of the surface?
Consider a nonconducting sphere and a concentric nonconducting spherical shell, shown in the figure. The inner sphere has non uniform charge density ρ1 = ρ0 / r, where ρ0 is a constant, in units of C/m2 and radius a. The outer spherical shell has uniform charge density ρ2 , inner radius b, and outer radius c.
Find the magnitude of the electric field inside the inner sphere, for r < a, in terms of the given variables, as needed.
Consider a nonconducting sphere and a concentric nonconducting spherical shell, shown in the figure. The inner sphere has non uniform charge density ρ1 = ρ0 / r, where ρ0 is a constant, in units of C/m2 and radius a. The outer spherical shell has uniform charge density ρ2 , inner radius b, and outer radius c.
Find the magnitude of the electric field for a < r < b, in terms of the given variables, as needed.
Chapter 23 Solutions
Physics for Scientists and Engineers
Ch. 23.2 - Suppose a point charge is located at the center of...Ch. 23.3 - If the net flux through a gaussian surface is...Ch. 23 - A negatively charged rod of finite length carries...Ch. 23 - A positively charged disk has a uniform charge per...Ch. 23 - A uniformly charged ring of radius 10.0 cm has a...Ch. 23 - The electric field along the axis of a uniformly...Ch. 23 - Example 23.3 derives the exact expression for the...Ch. 23 - A uniformly charged rod of length L and total...Ch. 23 - A continuous line of charge lies along the x axis,...Ch. 23 - A thin rod of length and uniform charge per unit...
Ch. 23 - (a) Consider a uniformly charged, thin-walled,...Ch. 23 - A vertical electric field of magnitude 2.00 104...Ch. 23 - A flat surface of area 3.20 m2 is rotated in a...Ch. 23 - A nonuniform electric field is given by the...Ch. 23 - An uncharged, nonconducting, hollow sphere of...Ch. 23 - Find the net electric flux through the spherical...Ch. 23 - Four closed surfaces, S1 through S4 together with...Ch. 23 - A charge of 170 C is at the center of a cube of...Ch. 23 - (a) Find the net electric flux through the cube...Ch. 23 - A particle with charge of 12.0 C is placed at the...Ch. 23 - A particle with charge Q = 5.00 C is located at...Ch. 23 - A particle with charge Q is located at the center...Ch. 23 - (a) A panicle with charge q is located a distance...Ch. 23 - Find the net electric flux through (a) the closed...Ch. 23 - Figure P23.23 represents the top view of a cubic...Ch. 23 - Determine the magnitude of the electric field at...Ch. 23 - In nuclear fission, a nucleus of uranium-238,...Ch. 23 - Suppose you fill two rubber balloons with air,...Ch. 23 - A large, flat, horizontal sheet of charge has a...Ch. 23 - A nonconducting wall carries charge with a uniform...Ch. 23 - A uniformly charged, straight filament 7.00 m in...Ch. 23 - You are working on a laboratory device that...Ch. 23 - Consider a long, cylindrical charge distribution...Ch. 23 - Assume the magnitude of the electric field on each...Ch. 23 - A solid sphere of radius 40.0 cm has a total...Ch. 23 - A cylindrical shell of radius 7.00 cm and length...Ch. 23 - You are working for the summer at a research...Ch. 23 - You are working for the summer at a research...Ch. 23 - Find the electric flux through the plane surface...Ch. 23 - Three solid plastic cylinders all have radius 2.50...Ch. 23 - A line of charge starts at x = +x0 and extends to...Ch. 23 - Show that the maximum magnitude Emax of the...Ch. 23 - A line of positive charge is formed into a...Ch. 23 - A very large conducting plate lying in the xy...Ch. 23 - A sphere of radius R = 1.00 m surrounds a particle...Ch. 23 - A sphere of radius R surrounds a particle with...Ch. 23 - A slab of insulating material has a nonuniform...Ch. 23 - A sphere of radius 2a is made of a nonconducting...Ch. 23 - An infinitely long insulating cylinder of radius R...Ch. 23 - A particle with charge Q is located on the axis of...Ch. 23 - Review. A slab of insulating material (infinite in...Ch. 23 - Identical thin rods of length 2a carry equal...Ch. 23 - A solid insulating sphere of radius R has a...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Similar questions
- Consider a spherical Gaussian surface of radius R centered at the origin. A charge Q is placed inside the sphere. Where should the charge be located to maximize the magnitude of the flux of the electric field through the Gaussian surface? A at x = 0, y = R/2, z = 0 B The flux does not depend on the position of the charge as long as it is inside the sphere C) at x = R/2, y = 0, z = 0 D) at x = 0, y = 0, z = R/2arrow_forwardAn imaginary cubical surface of side LL has its edges parallel to the x-, y- and z-axes, one corner at the point x=0, y=0, z=0 and the opposite corner at the point x=L, y=L ,z=L. The cube is in a region of uniform electric field E⃗ =E1iˆ+E2jˆ, where E1E1 and E2E2 are positive constants. Calculate the electric flux through (a) the cube face in the plane z=0, (b) the cube face in the plane z=L, and (c) the entire cubical surface. For each face the normal points out of the cube.arrow_forwardCompute the magnitude of the electric field at the point x = 30 cm on the x-axis.arrow_forward
- Consider an infinitely long, hollow cylinder, with inner radius R1 and outer radius Ra. the material of the cylinder is uniformly charged so that the cylinder has a charge per length. Finally, consider a solid cylinder of radius R, with a uniform charge density. What is the magnitude of the electric field inside the cylinder at a distance r from the center (r<R)?arrow_forwardA solid insulating sphere of radius 5 cm carries electric charge uniformly distributed throughout its volume. Concentric with the sphere is a conducting spherical shell with no net charge as shown in Figure OQ24.9. The inner radius of the shell is 10 cm, and the outer radius is 15 cm. No other charges are nearby. (a) Rank the magnitude of the electric Held at points A (at radius 4 cm), B (radius 8 cm), C (radius 12 cm), and I) (radius 16 cm) from largest to smallest. Display any cases of equality in your ranking, (b) Similarly rank the electric flux through concentric spherical surfaces through points A, B. C, and D.arrow_forwardSections AB and CD of a thin non-conducting ring of radius R are uniformly (with constant linear density) charged with charge + q and −q, respectively. The points ABCD form the vertices of the square. Find the electric field in the center of the ring.arrow_forward
- A thin nonconducting rod with a uniform distribution of positive charge Q is bent into a circle of radius R (see the figure). The central perpendicular axis through the ring is a z-axis, with the origin at the center of the ring. What is the magnitude of the electric field due to the rod at (a) z = 0 and (b) z = ∞? (c) In terms of R, at what positive value of z is that magnitude maximum? (d) If R = 2.06 cm and Q = 4.33 μC, what is the maximum magnitude?arrow_forwardA charge distribution that is spherically symmetric but not uniform radially produces an electric field of magnitude E = Kr4, directed radially outward from the center of the sphere. Here r is the radial distance from that center, and K is a constant.What is the volume density r of the charge distribution?arrow_forwardA conducting hollow sphere of internal radius a and external b has a total charge + 11q, determine the electric field between radius a and b in terms of ɛ0, q and the radius of the Gaussian r.arrow_forward
- Problem 6: A circular loop of radius R= 2 cm is centered at the origin where there is a constant electric field E = Egi + Eyj. For this problem, assume E,= 32 N/C and E, = 156 N/C. Part (a) What is the flux through the loop, in Nm2/C, when the loop is oriented so that its normal vector is in the x-direction? Part (b) What is the flux through the loop, in Nm2/C, when the loop is oriented so that its normal vector is in the negative y-direction? = Part (c) What is the flux through the loop, in Nm2/C, when the loop is oriented so that its normal vector is in the positive z-direction?arrow_forwardA Gaussian surface in the form of a hemisphere of radius R = 5.84 cm lies in a uniform electric field of magnitude E = 2.20 N/C. The surface encloses no net charge. At the (flat) base of the surface, the field is perpendicular to the surface and directed into the surface. (a) What is the flux through the base? ______________N · m2/C(b) What is the flux through the curved portion of the surface? _______________N · m2/Carrow_forwardA nonconducting spherical shell has an inner radius A, an outer radius B, and a nonuniform charge 6a density given by p = p3 +e-pr where a and B are constants. The inner spherical shell is surrounded with a concentric nonconducting spherical shell that has an inner radius B, outer radius C, and a uniform charge density such that the electric field for r> C is zero. 1. What is the total charge contained in the inner spherical shell? 2. What is the charge density in the outer spherical shell? 3. What is the magnitude of the electric field for A < r < B? 4. What is the magnitude of the electric field for Barrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
Recommended textbooks for you
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...
Physics
ISBN:9781133939146
Author:Katz, Debora M.
Publisher:Cengage Learning
Electric Fields: Crash Course Physics #26; Author: CrashCourse;https://www.youtube.com/watch?v=mdulzEfQXDE;License: Standard YouTube License, CC-BY