Chapter 2.2, Problem 45ES

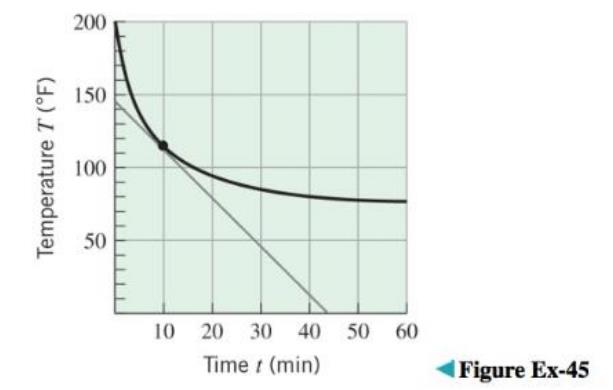
ssAccording to Newton’s Law of Cooling, the rate of change of an object’s temperature is proportional to the difference between the temperature of the object and that of the surrounding medium. The accompanying figure on the next page shows the graph of the temperature $T$ (in degrees Fahrenheit) versus time $t$ (in minutes) for a cup of coffee, initially with a temperature of $200°\text{F}$ , that is allowed to cool in a room with a constant temperature of $75°\text{F}$ .

(a) Estimate $T$ and $dT/dt$ when $t=10\text{ min}$ .

(b) Newton’s Law of Cooling can be expressed as

$\frac{dT}{dt}=k\left(T-T_0\right)$

where $k$ is the constant of proportionality and $T_0$ is the temperature (assumed constant) of the surrounding medium. Use the results in part (a) to estimate the value of $k$ .