EBK STATISTICS FOR BUSINESS & ECONOMICS
12th Edition
ISBN: 8220100460463
Author: Anderson
Publisher: CENGAGE L
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 21.3, Problem 13E
Lawson’s Department Store faces a buying decision for a seasonal product for which demand can be high, medium, or low. The purchaser for Lawson’s can order 1, 2, or 3 lots of the product before the season begins but cannot reorder later. Profit projections (in thousands of dollars) are shown.
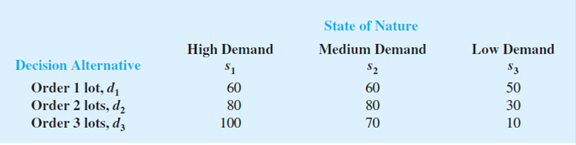
- a. If the prior probabilities for the three states of nature are .3, .3, and .4, respectively, what is the recommended order quantity?
- b. At each preseason sales meeting, the vice president of sales provides a personal opinion regarding potential demand for this product. Because of the vice president’s enthusiasm and optimistic nature, the predictions of market conditions have always been either “excellent” (E) or “very good” (V). Probabilities are as follows. What is the optimal decision strategy?
| P(E) = .7 | P(s1 | E ) = .34 | P(s1 | V ) = .20 |
| P(V) = .3 | P(s2 | E ) = .32 | P(s2 | V) = .26 |
| P(s3 | E) = .34 | P(s3 | V) = .54 |
- c. Compute EVPI and EVSI. Discuss whether the firm should consider a consulting expert who could provide independent forecasts of market conditions for the product.
Expert Solution & Answer
Trending nowThis is a popular solution!
Students have asked these similar questions
Throughout, A, B, (An, n≥ 1), and (Bn, n≥ 1) are subsets of 2.
1. Show that
AAB (ANB) U (BA) = (AUB) (AB),
Α' Δ Β = Α Δ Β,
{A₁ U A2} A {B₁ U B2) C (A1 A B₁}U{A2 A B2).
16. Show that, if X and Y are independent random variables, such that E|X|< ∞,
and B is an arbitrary Borel set, then
EXI{Y B} = EX P(YE B).
Proposition 1.1 Suppose that X1, X2,... are random variables. The following
quantities are random variables:
(a) max{X1, X2) and min(X1, X2);
(b) sup, Xn and inf, Xn;
(c) lim sup∞ X
and lim inf∞ Xn-
(d) If Xn(w) converges for (almost) every w as n→ ∞, then lim-
random variable.
→ Xn is a
Chapter 21 Solutions
EBK STATISTICS FOR BUSINESS & ECONOMICS
Ch. 21.2 - Prob. 1ECh. 21.2 - A decision maker faced with four decision...Ch. 21.2 - Hudson Corporation is considering three options...Ch. 21.2 - Myrtle Air Express decided to offer direct service...Ch. 21.2 - The distance from Potsdam to larger markets and...Ch. 21.2 - Seneca Hill Winery recently purchased land for the...Ch. 21.2 - The Lake Placid Town Council has decided to build...Ch. 21.3 - Consider a variation of the PDC decision tree...Ch. 21.3 - A real estate investor has the opportunity to...Ch. 21.3 - Dante Development Corporation is considering...
Ch. 21.3 - Hales TV Productions is considering producing a...Ch. 21.3 - Martins Service Station is considering entering...Ch. 21.3 - Lawsons Department Store faces a buying decision...Ch. 21.4 - Suppose that you are given a decision situation...Ch. 21.4 - In the following profit payoff table for a...Ch. 21.4 - To save on expenses, Rona and Jerry agreed to form...Ch. 21.4 - The Gorman Manufacturing Company must decide...Ch. 21 - An investor wants to select one of seven mutual...Ch. 21 - Warren Lloyd is interested in leasing a new car...Ch. 21 - Hemmingway, Inc. is considering a 50 million...Ch. 21 - Embassy Publishing Company received a six-chapter...Ch. 21 - Lawsuit Defense Strategy John Campbell, an...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, statistics and related others by exploring similar questions and additional content below.Similar questions
- Exercise 4.2 Prove that, if A and B are independent, then so are A and B, Ac and B, and A and B.arrow_forward8. Show that, if {Xn, n ≥ 1) are independent random variables, then sup X A) < ∞ for some A.arrow_forward8- 6. Show that, for any random variable, X, and a > 0, 8 心 P(xarrow_forward15. This problem extends Problem 20.6. Let X, Y be random variables with finite mean. Show that 00 (P(X ≤ x ≤ Y) - P(X ≤ x ≤ X))dx = E Y — E X.arrow_forward(b) Define a simple random variable. Provide an example.arrow_forward17. (a) Define the distribution of a random variable X. (b) Define the distribution function of a random variable X. (c) State the properties of a distribution function. (d) Explain the difference between the distribution and the distribution function of X.arrow_forward16. (a) Show that IA(w) is a random variable if and only if A E Farrow_forward15. Let 2 {1, 2,..., 6} and Fo({1, 2, 3, 4), (3, 4, 5, 6}). (a) Is the function X (w) = 21(3, 4) (w)+711.2,5,6) (w) a random variable? Explain. (b) Provide a function from 2 to R that is not a random variable with respect to (N, F). (c) Write the distribution of X. (d) Write and plot the distribution function of X.arrow_forward20. Define the o-field R2. Explain its relation to the o-field R.arrow_forward7. Show that An → A as n→∞ I{An} - → I{A} as n→ ∞.arrow_forward7. (a) Show that if A,, is an increasing sequence of measurable sets with limit A = Un An, then P(A) is an increasing sequence converging to P(A). (b) Repeat the same for a decreasing sequence. (c) Show that the following inequalities hold: P (lim inf An) lim inf P(A) ≤ lim sup P(A) ≤ P(lim sup A). (d) Using the above inequalities, show that if A, A, then P(A) + P(A).arrow_forward19. (a) Define the joint distribution and joint distribution function of a bivariate ran- dom variable. (b) Define its marginal distributions and marginal distribution functions. (c) Explain how to compute the marginal distribution functions from the joint distribution function.arrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
Recommended textbooks for you
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL
Continuous Probability Distributions - Basic Introduction; Author: The Organic Chemistry Tutor;https://www.youtube.com/watch?v=QxqxdQ_g2uw;License: Standard YouTube License, CC-BY
Probability Density Function (p.d.f.) Finding k (Part 1) | ExamSolutions; Author: ExamSolutions;https://www.youtube.com/watch?v=RsuS2ehsTDM;License: Standard YouTube License, CC-BY
Find the value of k so that the Function is a Probability Density Function; Author: The Math Sorcerer;https://www.youtube.com/watch?v=QqoCZWrVnbA;License: Standard Youtube License