
Concept explainers
(a)
To graph: The
(a)
Explanation of Solution
Given information: The piecewise function
Graph:
To graph a function
First press “ON” button on graphical calculator, press
Now, enter the key
The display will show the equation,
Adjust the window at
Now, press the
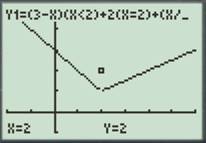
Figure (1)
Interpretation: The graph of the piecewise function
(b)
To find: The value of limits
(b)
Answer to Problem 58E
The value of limits
Explanation of Solution
Given information:
The piecewise function
Calculation:
As for the right side of the point
Use the function
Substitute
So, the value of
Now for the left side of the point
Use the function
Substitute
So, the value of
Therefore, the value of limits
(c)
To check: Whether the limits
(c)
Answer to Problem 58E
The limit
Explanation of Solution
Given information: The piecewise function
As calculated in part (b), the value of limits
The left hand limit for
Therefore, the limit
Chapter 2 Solutions
Calculus: Graphical, Numerical, Algebraic: Solutions Manual
Additional Math Textbook Solutions
College Algebra with Modeling & Visualization (5th Edition)
Thinking Mathematically (6th Edition)
Calculus: Early Transcendentals (2nd Edition)
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
Elementary Statistics: Picturing the World (7th Edition)
Elementary Statistics (13th Edition)
- Under certain conditions, the number of diseased cells N(t) at time t increases at a rate N'(t) = Aekt, where A is the rate of increase at time 0 (in cells per day) and k is a constant. (a) Suppose A = 60, and at 3 days, the cells are growing at a rate of 180 per day. Find a formula for the number of cells after t days, given that 200 cells are present at t = 0. (b) Use your answer from part (a) to find the number of cells present after 8 days. (a) Find a formula for the number of cells, N(t), after t days. N(t) = (Round any numbers in exponents to five decimal places. Round all other numbers to the nearest tenth.)arrow_forwardThe marginal revenue (in thousands of dollars) from the sale of x handheld gaming devices is given by the following function. R'(x) = 4x (x² +26,000) 2 3 (a) Find the total revenue function if the revenue from 125 devices is $17,939. (b) How many devices must be sold for a revenue of at least $50,000? (a) The total revenue function is R(x) = (Round to the nearest integer as needed.) given that the revenue from 125 devices is $17,939.arrow_forwardUse substitution to find the indefinite integral. S 2u √u-4 -du Describe the most appropriate substitution case and the values of u and du. Select the correct choice below and fill in the answer boxes within your choice. A. Substitute u for the quantity in the numerator. Let v = , so that dv = ( ) du. B. Substitute u for the quantity under the root. Let v = u-4, so that dv = (1) du. C. Substitute u for the quantity in the denominator. Let v = Use the substitution to evaluate the integral. so that dv= ' ( du. 2u -du= √√u-4arrow_forward
- Use substitution to find the indefinite integral. Зи u-8 du Describe the most appropriate substitution case and the values of u and du. Select the correct choice below and fill in the answer boxes within your choice. A. Substitute u for the quantity in the numerator. Let v = , so that dv = ( ( ) du. B. Substitute u for the quantity under the root. Let v = u-8, so that dv = (1) du. C. Substitute u for the quantity in the denominator. Let v = so that dv= ( ) du. Use the substitution to evaluate the integral. S Зи -du= u-8arrow_forwardFind the derivative of the function. 5 1 6 p(x) = -24x 5 +15xarrow_forward∞ 2n (4n)! Let R be the radius of convergence of the series -x2n. Then the value of (3" (2n)!)² n=1 sin(2R+4/R) is -0.892 0.075 0.732 -0.812 -0.519 -0.107 -0.564 0.588arrow_forward
- Find the cost function if the marginal cost function is given by C'(x) = x C(x) = 2/5 + 5 and 32 units cost $261.arrow_forwardFind the cost function if the marginal cost function is C'(x) = 3x-4 and the fixed cost is $9. C(x) = ☐arrow_forwardFor the power series ∞ (−1)" (2n+1)(x+4)” calculate Z, defined as follows: n=0 (5 - 1)√n if the interval of convergence is (a, b), then Z = sin a + sin b if the interval of convergence is (a, b), then Z = cos asin b if the interval of convergence is (a, b], then Z = sin a + cos b if the interval of convergence is [a, b], then Z = cos a + cos b Then the value of Z is -0.502 0.117 -0.144 -0.405 0.604 0.721 -0.950 -0.588arrow_forward
- H-/ test the Series 1.12 7√2 by ratio best 2n 2-12- nz by vitio test enarrow_forwardHale / test the Series 1.12 7√2 2n by ratio best 2-12- nz by vico tio test en - プ n2 rook 31() by mood fest 4- E (^)" by root test Inn 5-E 3' b. E n n³ 2n by ratio test ٤ by Comera beon Test (n+2)!arrow_forwardEvaluate the double integral ' √ √ (−2xy² + 3ry) dA R where R = {(x,y)| 1 ≤ x ≤ 3, 2 ≤ y ≤ 4} Double Integral Plot of integrand and Region R N 120 100 80- 60- 40 20 -20 -40 2 T 3 4 5123456 This plot is an example of the function over region R. The region and function identified in your problem will be slightly different. Answer = Round your answer to four decimal places.arrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





