COLLEGE ALGEBRA (PRINT UPGRADE)
6th Edition
ISBN: 2810000027802
Author: BITTINGER
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 2.1, Problem 35E
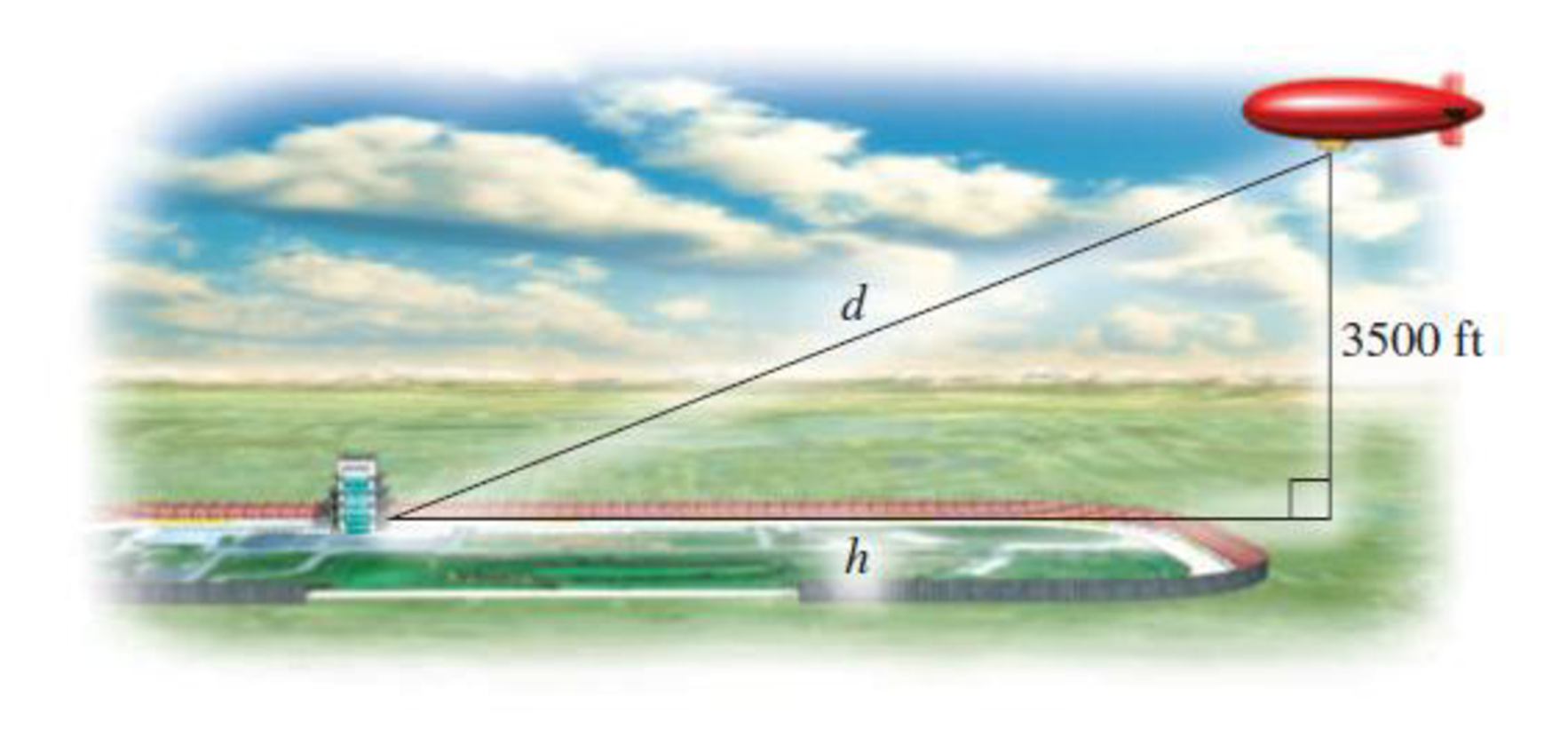
Blimp Distance. The Goodyear Blimp can be seen flying at an altitude of 3500 ft above the Motor Speedway during the Indianapolis 500 race. The slanted distance directly to the Pagoda at the start–finish line is d feet. Express the horizontal distance h as a function of d.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Please help me with these questions. I am having a hard time understanding what to do. Thank you
Answers
*************
*********************************
Q.1) Classify the following statements as a true or false statements:
a. If M is a module, then every proper submodule of M is contained in a maximal
submodule of M.
b. The sum of a finite family of small submodules of a module M is small in M.
c. Zz is directly indecomposable.
d. An epimorphism a: M→ N is called solit iff Ker(a) is a direct summand in M.
e. The Z-module has two composition series.
Z
6Z
f. Zz does not have a composition series.
g. Any finitely generated module is a free module.
h. If O→A MW→ 0 is short exact sequence then f is epimorphism.
i. If f is a homomorphism then f-1 is also a homomorphism.
Maximal C≤A if and only if is simple.
Sup
Q.4) Give an example and explain your claim in each case:
Monomorphism not split.
b) A finite free module.
c) Semisimple module.
d) A small submodule A of a module N and a homomorphism op: MN, but
(A) is not small in M.
Chapter 2 Solutions
COLLEGE ALGEBRA (PRINT UPGRADE)
Ch. 2.1 - Determine the intervals on which the function is...Ch. 2.1 - Determine the intervals on which the function is...Ch. 2.1 - Determine the intervals on which the function is...Ch. 2.1 - Determine the intervals on which the function is...Ch. 2.1 - Determine the intervals on which the function is...Ch. 2.1 - Determine the intervals on which the function is...Ch. 2.1 - Prob. 7ECh. 2.1 - Detemine the domain and the range of each of the...Ch. 2.1 - Detemine the domain and the range of each of the...Ch. 2.1 - Detemine the domain and the range of each of the...
Ch. 2.1 - Detemine the domain and the range of each of the...Ch. 2.1 - Detemine the domain and the range of each of the...Ch. 2.1 - Using the graph, determine any relative maxima or...Ch. 2.1 - Using the graph, determine any relative maxima or...Ch. 2.1 - Using the graph, determine any relative maxima or...Ch. 2.1 - Prob. 16ECh. 2.1 - Prob. 17ECh. 2.1 - Graph the function. Estimate the intervals on...Ch. 2.1 - Prob. 19ECh. 2.1 - Prob. 20ECh. 2.1 - Prob. 21ECh. 2.1 - Graph the function. Estimate the intervals on...Ch. 2.1 - Graph the function using the given viewing window....Ch. 2.1 - Graph the function using the given viewing window....Ch. 2.1 - Prob. 25ECh. 2.1 - Prob. 26ECh. 2.1 - Prob. 27ECh. 2.1 - Prob. 28ECh. 2.1 - Prob. 29ECh. 2.1 - Prob. 30ECh. 2.1 - Prob. 31ECh. 2.1 - Prob. 32ECh. 2.1 - Lumberyard. Ricks lumberyard has 480 yd of fencing...Ch. 2.1 - Triangular Flag. A seamstress is designing a...Ch. 2.1 - Blimp Distance. The Goodyear Blimp can be seen...Ch. 2.1 - Prob. 36ECh. 2.1 - Prob. 37ECh. 2.1 - Carpet Area. A carpet installer uses 46 ft of...Ch. 2.1 - Prob. 39ECh. 2.1 - Prob. 40ECh. 2.1 - Prob. 42ECh. 2.1 - Prob. 43ECh. 2.1 - Office File. Designs Unlimited plans to produce a...Ch. 2.1 - Prob. 45ECh. 2.1 - Prob. 46ECh. 2.1 - Prob. 47ECh. 2.1 - Prob. 48ECh. 2.1 - Prob. 49ECh. 2.1 - Prob. 50ECh. 2.1 - Graph each of the following functions. Check your...Ch. 2.1 - Prob. 52ECh. 2.1 - Prob. 53ECh. 2.1 - Prob. 54ECh. 2.1 - Prob. 55ECh. 2.1 - Prob. 56ECh. 2.1 - Prob. 57ECh. 2.1 - Prob. 58ECh. 2.1 - Graph each of the following functions. Check your...Ch. 2.1 - Graph each of the following functions. Check your...Ch. 2.1 - Prob. 61ECh. 2.1 - Prob. 62ECh. 2.1 - Prob. 63ECh. 2.1 - Prob. 64ECh. 2.1 - Prob. 65ECh. 2.1 - Prob. 66ECh. 2.1 - Prob. 67ECh. 2.1 - Prob. 68ECh. 2.1 - Find the domain and the range of each of the...Ch. 2.1 - Prob. 70ECh. 2.1 - Prob. 71ECh. 2.1 - Prob. 72ECh. 2.1 - Prob. 73ECh. 2.1 - Prob. 74ECh. 2.1 - Prob. 75ECh. 2.1 - Prob. 76ECh. 2.1 - Prob. 77ECh. 2.1 - Prob. 78ECh. 2.1 - Prob. 79ECh. 2.1 - Prob. 80ECh. 2.1 - Prob. 81ECh. 2.1 - Prob. 82ECh. 2.1 - Prob. 83ECh. 2.1 - Prob. 84ECh. 2.1 - Prob. 85ECh. 2.1 - Minimizing Power Line Costs. A power line is...Ch. 2.1 - Volume of an Inscribed Cylinder. A right circular...Ch. 2.2 - Prob. 1ECh. 2.2 - Given that f(x) = x2 3 and g(x) = 2x + 1, find...Ch. 2.2 - Given that f(x) = x2 3 and g(x) = 2x + 1, find...Ch. 2.2 - Given that f(x) = x2 3 and g(x) = 2x + 1, find...Ch. 2.2 - Prob. 5ECh. 2.2 - Prob. 6ECh. 2.2 - Prob. 7ECh. 2.2 - Prob. 8ECh. 2.2 - Prob. 9ECh. 2.2 - Prob. 10ECh. 2.2 - Prob. 11ECh. 2.2 - Given that h(x) = x + 4 and g(x)=x1, find each of...Ch. 2.2 - Prob. 13ECh. 2.2 - Prob. 14ECh. 2.2 - Prob. 15ECh. 2.2 - Prob. 16ECh. 2.2 - Prob. 17ECh. 2.2 - For each pair of functions in Exercises 1734: a)...Ch. 2.2 - Prob. 19ECh. 2.2 - For each pair of functions in Exercises 1734: a)...Ch. 2.2 - Prob. 21ECh. 2.2 - For each pair of functions in Exercises 1734: a)...Ch. 2.2 - Prob. 23ECh. 2.2 - For each pair of functions in Exercises 1734: a)...Ch. 2.2 - Prob. 25ECh. 2.2 - For each pair of functions in Exercises 1734: a)...Ch. 2.2 - Prob. 27ECh. 2.2 - For each pair of functions in Exercises 1734: a)...Ch. 2.2 - Prob. 29ECh. 2.2 - For each pair of functions in Exercises 1734: a)...Ch. 2.2 - Prob. 31ECh. 2.2 - For each pair of functions in Exercises 1734: a)...Ch. 2.2 - Prob. 33ECh. 2.2 - Prob. 34ECh. 2.2 - In Exercises 3540, consider the functions F and G...Ch. 2.2 - In Exercises 3540, consider the functions F and G...Ch. 2.2 - In Exercises 3540, consider the functions F and G...Ch. 2.2 - In Exercises 3540, consider the functions F and G...Ch. 2.2 - In Exercises 3540, consider the functions F and G...Ch. 2.2 - In Exercises 3540, consider the functions F and G...Ch. 2.2 - In Exercises 4146, consider the functions F and G...Ch. 2.2 - Prob. 42ECh. 2.2 - In Exercises 4146, consider the functions F and G...Ch. 2.2 - In Exercises 4146, consider the functions F and G...Ch. 2.2 - Prob. 45ECh. 2.2 - Prob. 46ECh. 2.2 - Prob. 47ECh. 2.2 - Total Cost, Revenue, and Profit. Given that R(x) =...Ch. 2.2 - For each function f, construct and simplify the...Ch. 2.2 - Prob. 50ECh. 2.2 - For each function f, construct and simplify the...Ch. 2.2 - Prob. 52ECh. 2.2 - Prob. 53ECh. 2.2 - For each function f, construct and simplify the...Ch. 2.2 - Prob. 55ECh. 2.2 - Prob. 56ECh. 2.2 - For each function f, construct and simplify the...Ch. 2.2 - Prob. 58ECh. 2.2 - For each function f, construct and simplify the...Ch. 2.2 - For each function f, construct and simplify the...Ch. 2.2 - Prob. 61ECh. 2.2 - Prob. 62ECh. 2.2 - For each function f, construct and simplify the...Ch. 2.2 - Prob. 64ECh. 2.2 - Prob. 65ECh. 2.2 - For each function f, construct and simplify the...Ch. 2.2 - Prob. 67ECh. 2.2 - Prob. 68ECh. 2.2 - For each function f, construct and simplify the...Ch. 2.2 - Prob. 70ECh. 2.2 - Prob. 71ECh. 2.2 - Prob. 72ECh. 2.2 - Prob. 73ECh. 2.2 - Prob. 74ECh. 2.2 - Prob. 75ECh. 2.2 - Prob. 76ECh. 2.2 - Prob. 77ECh. 2.3 - Given that f(x)=3x+1, g(x)=x22x6, and h(x)=x3,...Ch. 2.3 - Prob. 2ECh. 2.3 - Given that f(x)=3x+1, g(x)=x22x6, and h(x)=x3,...Ch. 2.3 - Given that f(x)=3x+1, g(x)=x22x6, and h(x)=x3,...Ch. 2.3 - Prob. 5ECh. 2.3 - Given that f(x)=3x+1, g(x)=x22x6, and h(x)=x3,...Ch. 2.3 - Prob. 7ECh. 2.3 - Prob. 8ECh. 2.3 - Given that f(x)=3x+1, g(x)=x22x6, and h(x)=x3,...Ch. 2.3 - Prob. 10ECh. 2.3 - Prob. 11ECh. 2.3 - Given that f(x)=3x+1, g(x)=x22x6, and h(x)=x3,...Ch. 2.3 - Prob. 13ECh. 2.3 - Prob. 14ECh. 2.3 - Given that f(x)=3x+1, g(x)=x22x6, and h(x)=x3,...Ch. 2.3 - Prob. 16ECh. 2.3 - Prob. 17ECh. 2.3 - Find (fg)(x) and (gf)(x) and the domain of each....Ch. 2.3 - Prob. 19ECh. 2.3 - Prob. 20ECh. 2.3 - Find (fg)(x) and (gf)(x) and the domain of each....Ch. 2.3 - Prob. 22ECh. 2.3 - Prob. 23ECh. 2.3 - Find (fg)(x) and (gf)(x) and the domain of each....Ch. 2.3 - Find (fg)(x) and (gf)(x) and the domain of each....Ch. 2.3 - Prob. 26ECh. 2.3 - Find (fg)(x) and (gf)(x) and the domain of each....Ch. 2.3 - Prob. 28ECh. 2.3 - Find (fg)(x) and (gf)(x) and the domain of each....Ch. 2.3 - Find (fg)(x) and (gf)(x) and the domain of each....Ch. 2.3 - Prob. 31ECh. 2.3 - Prob. 32ECh. 2.3 - Find (fg)(x) and (gf)(x) and the domain of each....Ch. 2.3 - Prob. 34ECh. 2.3 - Prob. 35ECh. 2.3 - Find (fg)(x) and (gf)(x) and the domain of each....Ch. 2.3 - Find (fg)(x) and (gf)(x) and the domain of each....Ch. 2.3 - Prob. 38ECh. 2.3 - Find f(x) and g(x) such that h(x) = (f g)(x)....Ch. 2.3 - Prob. 40ECh. 2.3 - Prob. 41ECh. 2.3 - Find f(x) and g(x) such that h(x) = (f g)(x)....Ch. 2.3 - Find f(x) and g(x) such that h(x) = (f g)(x)....Ch. 2.3 - Prob. 44ECh. 2.3 - Find f(x) and g(x) such that h(x) = (f g)(x)....Ch. 2.3 - Prob. 46ECh. 2.3 - Find f(x) and g(x) such that h(x) = (f g)(x)....Ch. 2.3 - Find f(x) and g(x) such that h(x) = (f g)(x)....Ch. 2.3 - Find f(x) and g(x) such that h(x) = (f g)(x)....Ch. 2.3 - Prob. 50ECh. 2.3 - Ripple Spread. A stone is thrown into a pond,...Ch. 2.3 - The surface area S of a right circular cylinder is...Ch. 2.3 - Prob. 53ECh. 2.3 - Prob. 54ECh. 2.3 - Prob. 55ECh. 2.3 - Prob. 56ECh. 2.3 - Prob. 57ECh. 2.3 - Consider the following linear equations. Without...Ch. 2.3 - Prob. 59ECh. 2.3 - Prob. 60ECh. 2.3 - Prob. 61ECh. 2.3 - Prob. 62ECh. 2.3 - Prob. 63ECh. 2.3 - Prob. 64ECh. 2.4 - Determine visually whether the graph is symmetric...Ch. 2.4 - Prob. 2ECh. 2.4 - Prob. 3ECh. 2.4 - Prob. 4ECh. 2.4 - Determine visually whether the graph is symmetric...Ch. 2.4 - Prob. 6ECh. 2.4 - Prob. 7ECh. 2.4 - Prob. 8ECh. 2.4 - Prob. 9ECh. 2.4 - Prob. 10ECh. 2.4 - Prob. 11ECh. 2.4 - Prob. 12ECh. 2.4 - Prob. 13ECh. 2.4 - Prob. 14ECh. 2.4 - Prob. 15ECh. 2.4 - Prob. 16ECh. 2.4 - Prob. 17ECh. 2.4 - Prob. 18ECh. 2.4 - Prob. 19ECh. 2.4 - Prob. 20ECh. 2.4 - Prob. 21ECh. 2.4 - Prob. 22ECh. 2.4 - Prob. 23ECh. 2.4 - Prob. 24ECh. 2.4 - Prob. 25ECh. 2.4 - Prob. 26ECh. 2.4 - Prob. 27ECh. 2.4 - Prob. 28ECh. 2.4 - Prob. 29ECh. 2.4 - Prob. 30ECh. 2.4 - Prob. 31ECh. 2.4 - Prob. 32ECh. 2.4 - Prob. 33ECh. 2.4 - Prob. 34ECh. 2.4 - Prob. 35ECh. 2.4 - Determine visually whether the function is even,...Ch. 2.4 - Prob. 37ECh. 2.4 - Prob. 38ECh. 2.4 - Prob. 39ECh. 2.4 - Prob. 40ECh. 2.4 - Prob. 41ECh. 2.4 - Prob. 42ECh. 2.4 - Prob. 43ECh. 2.4 - Prob. 44ECh. 2.4 - Determine algebraically whether the function is...Ch. 2.4 - Prob. 46ECh. 2.4 - Prob. 47ECh. 2.4 - Prob. 48ECh. 2.4 - Graph: f(x)={x2forx1,3,for1x2,x,forx2.Ch. 2.4 - Peace Corps Volunteers. Since 1961, there has been...Ch. 2.4 - Determine whether the function is even, odd, or...Ch. 2.4 - Determine whether the function is even, odd. or...Ch. 2.4 - Determine whether the graph is symmetric with...Ch. 2.4 - Determine whether the graph is symmetric with...Ch. 2.4 - Show that if f is any function, then the function...Ch. 2.4 - Show that if f is any function, then the function...Ch. 2.4 - Consider the functions E and O of Exercises 55 and...Ch. 2.4 - Determine whether the statement is true or false....Ch. 2.4 - Prob. 59ECh. 2.4 - Prob. 60ECh. 2.5 - Describe how the graph of the function can be...Ch. 2.5 - Describe how the graph of the function can be...Ch. 2.5 - Describe how the graph of the function can be...Ch. 2.5 - Prob. 4ECh. 2.5 - Describe how the graph of the function can be...Ch. 2.5 - Prob. 6ECh. 2.5 - Prob. 7ECh. 2.5 - Describe how the graph of the function can be...Ch. 2.5 - Describe how the graph of the function can be...Ch. 2.5 - Prob. 10ECh. 2.5 - Prob. 11ECh. 2.5 - Prob. 12ECh. 2.5 - Prob. 13ECh. 2.5 - Prob. 14ECh. 2.5 - Prob. 15ECh. 2.5 - Prob. 16ECh. 2.5 - Prob. 17ECh. 2.5 - Prob. 18ECh. 2.5 - Prob. 19ECh. 2.5 - Prob. 20ECh. 2.5 - Prob. 21ECh. 2.5 - Prob. 22ECh. 2.5 - Prob. 23ECh. 2.5 - Prob. 24ECh. 2.5 - Describe how the graph of the function can be...Ch. 2.5 - Prob. 26ECh. 2.5 - Prob. 27ECh. 2.5 - Prob. 28ECh. 2.5 - Prob. 29ECh. 2.5 - Describe how the graph of the function can be...Ch. 2.5 - Prob. 31ECh. 2.5 - Prob. 32ECh. 2.5 - Prob. 33ECh. 2.5 - Prob. 34ECh. 2.5 - Prob. 35ECh. 2.5 - Prob. 36ECh. 2.5 - Prob. 37ECh. 2.5 - Prob. 38ECh. 2.5 - Prob. 39ECh. 2.5 - Prob. 40ECh. 2.5 - Prob. 41ECh. 2.5 - Prob. 42ECh. 2.5 - Prob. 43ECh. 2.5 - Prob. 44ECh. 2.5 - Prob. 45ECh. 2.5 - Prob. 46ECh. 2.5 - Prob. 47ECh. 2.5 - Prob. 48ECh. 2.5 - Prob. 49ECh. 2.5 - Prob. 50ECh. 2.5 - Prob. 51ECh. 2.5 - Prob. 52ECh. 2.5 - Prob. 53ECh. 2.5 - Prob. 54ECh. 2.5 - Prob. 55ECh. 2.5 - Prob. 56ECh. 2.5 - Prob. 57ECh. 2.5 - Prob. 58ECh. 2.5 - Prob. 59ECh. 2.5 - Prob. 60ECh. 2.5 - Prob. 61ECh. 2.5 - Prob. 62ECh. 2.5 - Prob. 63ECh. 2.5 - Prob. 64ECh. 2.5 - Prob. 65ECh. 2.5 - A graph of y=f(x) follows. No formula for f is...Ch. 2.5 - Prob. 67ECh. 2.5 - Prob. 68ECh. 2.5 - Prob. 69ECh. 2.5 - Prob. 70ECh. 2.5 - Prob. 71ECh. 2.5 - Prob. 72ECh. 2.5 - Prob. 73ECh. 2.5 - Prob. 74ECh. 2.5 - Prob. 75ECh. 2.5 - Prob. 76ECh. 2.5 - Prob. 77ECh. 2.5 - Prob. 78ECh. 2.5 - Prob. 79ECh. 2.5 - Prob. 80ECh. 2.5 - Prob. 81ECh. 2.5 - Prob. 82ECh. 2.5 - Prob. 83ECh. 2.5 - Prob. 84ECh. 2.5 - Prob. 85ECh. 2.5 - Prob. 86ECh. 2.5 - Prob. 87ECh. 2.5 - Prob. 88ECh. 2.5 - Prob. 89ECh. 2.5 - Prob. 90ECh. 2.5 - Prob. 91ECh. 2.5 - Prob. 92ECh. 2.5 - Prob. 93ECh. 2.5 - Prob. 94ECh. 2.5 - Graph each of the following using a graphing...Ch. 2.5 - Prob. 96ECh. 2.5 - Prob. 97ECh. 2.5 - Prob. 98ECh. 2.6 - Find the variation constant and an equation of...Ch. 2.6 - Find the variation constant and an equation of...Ch. 2.6 - Prob. 3ECh. 2.6 - Prob. 4ECh. 2.6 - Prob. 5ECh. 2.6 - Prob. 6ECh. 2.6 - Prob. 7ECh. 2.6 - Prob. 8ECh. 2.6 - Prob. 9ECh. 2.6 - Prob. 10ECh. 2.6 - Prob. 11ECh. 2.6 - Prob. 12ECh. 2.6 - Prob. 13ECh. 2.6 - Prob. 14ECh. 2.6 - Prob. 15ECh. 2.6 - Prob. 16ECh. 2.6 - Prob. 17ECh. 2.6 - House of Representatives. The number of...Ch. 2.6 - Prob. 19ECh. 2.6 - Prob. 20ECh. 2.6 - Prob. 21ECh. 2.6 - Prob. 22ECh. 2.6 - Musical Pitch. The pitch P of a musical tone...Ch. 2.6 - Prob. 24ECh. 2.6 - Prob. 25ECh. 2.6 - Prob. 26ECh. 2.6 - Prob. 27ECh. 2.6 - Prob. 28ECh. 2.6 - Prob. 29ECh. 2.6 - Prob. 30ECh. 2.6 - Prob. 31ECh. 2.6 - Prob. 32ECh. 2.6 - Prob. 33ECh. 2.6 - Prob. 34ECh. 2.6 - Prob. 35ECh. 2.6 - Prob. 36ECh. 2.6 - Prob. 37ECh. 2.6 - Prob. 38ECh. 2.6 - Prob. 39ECh. 2.6 - Prob. 40ECh. 2.6 - In each of Exercises 4145, fill in the blank with...Ch. 2.6 - Prob. 42ECh. 2.6 - Prob. 43ECh. 2.6 - Prob. 44ECh. 2.6 - Prob. 45ECh. 2.6 - Prob. 46ECh. 2.6 - Prob. 47ECh. 2.6 - Prob. 48ECh. 2.6 - Prob. 49ECh. 2 - Determine whether the statement is true or false....Ch. 2 - Determine whether the statement is true or false....Ch. 2 - Determine whether the statement is true or false....Ch. 2 - Prob. 4MCCh. 2 - Prob. 5MCCh. 2 - Determine the domain and the range of the function...Ch. 2 - Prob. 7MCCh. 2 - For the function defined as...Ch. 2 - Prob. 9MCCh. 2 - Prob. 10MCCh. 2 - Given that f(x) = 3x 1 and g(x) = x2 + 4, find...Ch. 2 - Prob. 12MCCh. 2 - Prob. 13MCCh. 2 - Prob. 14MCCh. 2 - For each pair of functions in Exercises 14 and 15:...Ch. 2 - Prob. 16MCCh. 2 - For each function f in Exercises 16 and 17,...Ch. 2 - Prob. 18MCCh. 2 - Given that f(x) = 5x 4, g(x) = x3 + 1, and h(x) =...Ch. 2 - Prob. 20MCCh. 2 - Prob. 21MCCh. 2 - Prob. 22MCCh. 2 - Find (f g) (x) and (g f) (x) and the domain of...Ch. 2 - Prob. 1RECh. 2 - Prob. 2RECh. 2 - Prob. 3RECh. 2 - Prob. 4RECh. 2 - Prob. 5RECh. 2 - Prob. 6RECh. 2 - Prob. 7RECh. 2 - Prob. 8RECh. 2 - Prob. 9RECh. 2 - Prob. 10RECh. 2 - Prob. 11RECh. 2 - Prob. 12RECh. 2 - Prob. 13RECh. 2 - Prob. 14RECh. 2 - Prob. 15RECh. 2 - Prob. 16RECh. 2 - Prob. 17RECh. 2 - Prob. 18RECh. 2 - Prob. 19RECh. 2 - Prob. 20RECh. 2 - Prob. 21RECh. 2 - Prob. 22RECh. 2 - Prob. 23RECh. 2 - Prob. 24RECh. 2 - Prob. 25RECh. 2 - Prob. 26RECh. 2 - Prob. 27RECh. 2 - Prob. 28RECh. 2 - Prob. 29RECh. 2 - Prob. 30RECh. 2 - Prob. 31RECh. 2 - Prob. 32RECh. 2 - Prob. 33RECh. 2 - Prob. 34RECh. 2 - Prob. 35RECh. 2 - Prob. 36RECh. 2 - Prob. 37RECh. 2 - Prob. 38RECh. 2 - Prob. 39RECh. 2 - Prob. 40RECh. 2 - Prob. 41RECh. 2 - Prob. 42RECh. 2 - Prob. 43RECh. 2 - Prob. 44RECh. 2 - Prob. 45RECh. 2 - Prob. 46RECh. 2 - Prob. 47RECh. 2 - Prob. 48RECh. 2 - Prob. 49RECh. 2 - Prob. 50RECh. 2 - Prob. 51RECh. 2 - Prob. 52RECh. 2 - Prob. 53RECh. 2 - Prob. 54RECh. 2 - Prob. 55RECh. 2 - Prob. 56RECh. 2 - Prob. 57RECh. 2 - Prob. 58RECh. 2 - Prob. 59RECh. 2 - Prob. 60RECh. 2 - Prob. 61RECh. 2 - Prob. 62RECh. 2 - Prob. 63RECh. 2 - Prob. 64RECh. 2 - Prob. 65RECh. 2 - Prob. 66RECh. 2 - Prob. 67RECh. 2 - Prob. 68RECh. 2 - Prob. 69RECh. 2 - Prob. 70RECh. 2 - Prob. 71RECh. 2 - Prob. 72RECh. 2 - Prob. 73RECh. 2 - Prob. 74RECh. 2 - Prob. 75RECh. 2 - Prob. 76RECh. 2 - Prob. 77RECh. 2 - Prob. 78RECh. 2 - The graph of the function f is shown below. The...Ch. 2 - Prob. 80RECh. 2 - Prob. 81RECh. 2 - Prob. 82RECh. 2 - Prob. 83RECh. 2 - Prob. 84RECh. 2 - Prob. 85RECh. 2 - Prob. 86RECh. 2 - Prob. 87RECh. 2 - Prob. 1TCh. 2 - Prob. 2TCh. 2 - Prob. 3TCh. 2 - Prob. 4TCh. 2 - Prob. 5TCh. 2 - Prob. 6TCh. 2 - Prob. 7TCh. 2 - Prob. 8TCh. 2 - Prob. 9TCh. 2 - Prob. 10TCh. 2 - Prob. 11TCh. 2 - Prob. 12TCh. 2 - Prob. 13TCh. 2 - Prob. 14TCh. 2 - Prob. 15TCh. 2 - Prob. 16TCh. 2 - Prob. 17TCh. 2 - Prob. 18TCh. 2 - Prob. 19TCh. 2 - Prob. 20TCh. 2 - Prob. 21TCh. 2 - Prob. 22TCh. 2 - Prob. 23TCh. 2 - Prob. 24TCh. 2 - Prob. 25TCh. 2 - Prob. 26TCh. 2 - Prob. 27TCh. 2 - Prob. 28TCh. 2 - Prob. 29TCh. 2 - Prob. 30TCh. 2 - Prob. 31TCh. 2 - Prob. 32TCh. 2 - Prob. 33TCh. 2 - Prob. 34TCh. 2 - Prob. 35TCh. 2 - Prob. 36TCh. 2 - Prob. 37TCh. 2 - Prob. 38TCh. 2 - Prob. 39TCh. 2 - If (3, 1) is a point on the graph of y = f(x),...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, algebra and related others by exploring similar questions and additional content below.Similar questions
- I need diagram with solutionsarrow_forwardT. Determine the least common denominator and the domain for the 2x-3 10 problem: + x²+6x+8 x²+x-12 3 2x 2. Add: + Simplify and 5x+10 x²-2x-8 state the domain. 7 3. Add/Subtract: x+2 1 + x+6 2x+2 4 Simplify and state the domain. x+1 4 4. Subtract: - Simplify 3x-3 x²-3x+2 and state the domain. 1 15 3x-5 5. Add/Subtract: + 2 2x-14 x²-7x Simplify and state the domain.arrow_forwardQ.1) Classify the following statements as a true or false statements: Q a. A simple ring R is simple as a right R-module. b. Every ideal of ZZ is small ideal. very den to is lovaginz c. A nontrivial direct summand of a module cannot be large or small submodule. d. The sum of a finite family of small submodules of a module M is small in M. e. The direct product of a finite family of projective modules is projective f. The sum of a finite family of large submodules of a module M is large in M. g. Zz contains no minimal submodules. h. Qz has no minimal and no maximal submodules. i. Every divisible Z-module is injective. j. Every projective module is a free module. a homomorp cements Q.4) Give an example and explain your claim in each case: a) A module M which has a largest proper submodule, is directly indecomposable. b) A free subset of a module. c) A finite free module. d) A module contains no a direct summand. e) A short split exact sequence of modules.arrow_forward
- Listen ANALYZING RELATIONSHIPS Describe the x-values for which (a) f is increasing or decreasing, (b) f(x) > 0 and (c) f(x) <0. y Af -2 1 2 4x a. The function is increasing when and decreasing whenarrow_forwardBy forming the augmented matrix corresponding to this system of equations and usingGaussian elimination, find the values of t and u that imply the system:(i) is inconsistent.(ii) has infinitely many solutions.(iii) has a unique solutiona=2 b=1arrow_forwardif a=2 and b=1 1) Calculate 49(B-1)2+7B−1AT+7ATB−1+(AT)2 2)Find a matrix C such that (B − 2C)-1=A 3) Find a non-diagonal matrix E ̸= B such that det(AB) = det(AE)arrow_forwardWrite the equation line shown on the graph in slope, intercept form.arrow_forward1.2.15. (!) Let W be a closed walk of length at least 1 that does not contain a cycle. Prove that some edge of W repeats immediately (once in each direction).arrow_forward1.2.18. (!) Let G be the graph whose vertex set is the set of k-tuples with elements in (0, 1), with x adjacent to y if x and y differ in exactly two positions. Determine the number of components of G.arrow_forward1.2.17. (!) Let G,, be the graph whose vertices are the permutations of (1,..., n}, with two permutations a₁, ..., a,, and b₁, ..., b, adjacent if they differ by interchanging a pair of adjacent entries (G3 shown below). Prove that G,, is connected. 132 123 213 312 321 231arrow_forward1.2.19. Let and s be natural numbers. Let G be the simple graph with vertex set Vo... V„−1 such that v; ↔ v; if and only if |ji| Є (r,s). Prove that S has exactly k components, where k is the greatest common divisor of {n, r,s}.arrow_forward1.2.20. (!) Let u be a cut-vertex of a simple graph G. Prove that G - v is connected. עarrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
Recommended textbooks for you
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
College Algebra (MindTap Course List)
Algebra
ISBN:9781305652231
Author:R. David Gustafson, Jeff Hughes
Publisher:Cengage Learning
Area Between The Curve Problem No 1 - Applications Of Definite Integration - Diploma Maths II; Author: Ekeeda;https://www.youtube.com/watch?v=q3ZU0GnGaxA;License: Standard YouTube License, CC-BY