
Two forces are applied as shown to a hook. Determine graphically the magnitude and direction of their resultant using (a) the parallelogram law, (b) the triangle rule.
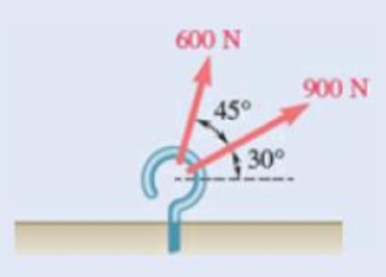
Fig. P2.1
(a)
The magnitude and direction of the resultant force on the hook graphically using the parallelogram law.
Answer to Problem 2.1P
The magnitude of the resultant force on the hook determined graphically using the parallelogram law is
Explanation of Solution
Force is a vector and the addition of vectors can be done using parallelogram law. The parallelogram law of vector addition says that if a parallelogram is constructed using two vectors by taking them as the adjacent sides of the parallelogram by attaching them on the same point, then the diagonal passing through that point gives the sum of the two vectors.
The forces acting on the hook are taken as the adjacent sides of the parallelogram. The diagram is shown in figure 1. In the figure,
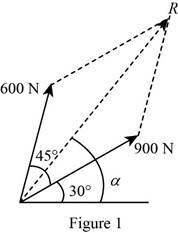
The length of the diagonal of the parallelogram gives the magnitude of the resultant vector and the angle the diagonal makes with the horizontal gives the direction.
Conclusion:
The length of the diagonal is measured to be
Thus, the magnitude of the resultant force on the hook determined graphically using the parallelogram law is
(b)
The magnitude and direction of the resultant force on the hook graphically using the triangle rule.
Answer to Problem 2.1P
The magnitude of the resultant force on the hook determined graphically using the triangle rule is
Explanation of Solution
Force is a vector and one of the graphical methods to obtain the resultant of two vectors is triangle rule. The triangle rule says that the sum of two vectors can be found by arranging the vectors in tip-to-tail fashion and then connecting the tail of the first vector with the tip of the second.
The forces acting on the hook are arranged in tip-to-tail fashion by placing the tail of
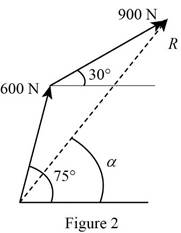
The length of the third side of the triangle formed gives the magnitude of the resultant force. The direction of the resultant force is specified by the angle the third side of the triangle makes with the horizontal.
Conclusion:
The length of the third side of the triangle is measured to be
Thus, the magnitude of the resultant force on the hook determined graphically using the triangle rule is
Want to see more full solutions like this?
Chapter 2 Solutions
Vector Mechanics for Engineers: Statics and Dynamics
Additional Engineering Textbook Solutions
Vector Mechanics For Engineers
Starting Out with C++: Early Objects (9th Edition)
Starting Out with Java: From Control Structures through Data Structures (4th Edition) (What's New in Computer Science)
Fluid Mechanics: Fundamentals and Applications
Elementary Surveying: An Introduction To Geomatics (15th Edition)
Starting Out with Programming Logic and Design (5th Edition) (What's New in Computer Science)
- (b) A steel 'hot rolled structural hollow section' column of length 5.75 m, has the cross-section shown in Figure Q.5(b) and supports a load of 750 kN. During service, it is subjected to axial compression loading where one end of the column is effectively restrained in position and direction (fixed) and the other is effectively held in position but not in direction (pinned). i) Given that the steel has a design strength of 275 MN/m², determine the load factor for the structural member based upon the BS5950 design approach using Datasheet Q.5(b). [11] ii) Determine the axial load that can be supported by the column using the Rankine-Gordon formula, given that the yield strength of the material is 280 MN/m² and the constant *a* is 1/30000. [6] 300 600 2-300 mm wide x 5 mm thick plates. Figure Q.5(b) L=5.75m Pinned Fixedarrow_forwardHelp ارجو مساعدتي في حل هذا السؤالarrow_forwardHelp ارجو مساعدتي في حل هذا السؤالarrow_forward
- Q2: For the following figure, find the reactions of the system. The specific weight of the plate is 500 lb/ft³arrow_forwardQ1: For the following force system, find the moments with respect to axes x, y, and zarrow_forwardQ10) Body A weighs 600 lb contact with smooth surfaces at D and E. Determine the tension in the cord and the forces acting on C on member BD, also calculate the reaction at B and F. Cable 6' 3' wwwarrow_forward
- Help ارجو مساعدتي في حل هذا السؤالarrow_forwardQ3: Find the resultant of the force system.arrow_forwardQuestion 1 A three-blade propeller of a diameter of 2 m has an activity factor AF of 200 and its ratio of static thrust coefficient to static torque coefficient is 10. The propeller's integrated lift coefficient is 0.3.arrow_forward
- (L=6847 mm, q = 5331 N/mm, M = 1408549 N.mm, and El = 8.6 x 1014 N. mm²) X A ΕΙ B L Y Marrow_forwardCalculate the maximum shear stress Tmax at the selected element within the wall (Fig. Q3) if T = 26.7 KN.m, P = 23.6 MPa, t = 2.2 mm, R = 2 m. The following choices are provided in units of MPa and rounded to three decimal places. Select one: ○ 1.2681.818 O 2. 25745.455 O 3. 17163.636 O 4. 10727.273 ○ 5.5363.636arrow_forwardIf L-719.01 mm, = 7839.63 N/m³, the normal stress σ caused by self-weight at the location of the maximum normal stress in the bar can be calculated as (Please select the correct value of σ given in Pa and rounded to three decimal places.) Select one: ○ 1. 1409.193 2. 845.516 O 3. 11273.545 ○ 4.8455.159 ○ 5.4509.418 6. 2818.386 7.5636.772arrow_forward
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





