
a.
Calculate the class width for the data on count of three-syllable words in advertising copy of magazine advertisements.
a.
Answer to Problem 20P
The class width is calculated as 6.
Explanation of Solution
Calculation:
From the given data set, the largest data point is 43 and the smallest data point is 0.
Class Width:
The class width is calculated as follows:
b.
Create a table for frequency distribution with class limits, class boundaries, midpoints, frequencies, relative frequencies, and cumulative frequencies.
b.
Answer to Problem 20P
The class limits for a frequency table with 8 classes using class width 6 are 0-5, 6-11, 12-17, 18-23, 24-29, 30-35, 36-41, and 42-47.
Explanation of Solution
Class limits:
Class limits are the maximum and minimum values in the class interval
Class Boundaries:
A class boundary is the midpoint between the upper limit of one class and the lower limit of the next class where the upper limit of the preceding class interval and the lower limit of the next class interval will be equal. The upper class boundary is calculated by adding 0.5 to the upper class limit and the lower class boundary is calculated by subtracting 0.5 from the lower class limit.
Midpoint:
The midpoint is calculated as given below:
Frequency:
Frequency is the number of data points that fall under each class.
Cumulative frequency:
Cumulative frequency is calculated by adding each frequency to the sum of preceding frequencies.
Relative Frequency:
Relative frequency is the ratio of frequency by the total number of data values.
The class width is 6. Hence, the lower class limit for the second class 6 is calculated by adding 6 to 0. Following this pattern, all the lower class limits are established. Then, the upper class limits are calculated.
The frequency distribution table is given below:
| Class Limits | Class Boundaries | Midpoints | Frequency | Relative Frequency | Cumulative Frequency |
| 0-5 | 0.5-5.5 |
2.5 | 13 | 13 | |
| 6-11 | 5.5-11.5 | 8.5 | 15 | 28 (=15+13) | |
| 12-17 | 11.5-17.5 | 14.5 | 11 | 39 (=11+28) | |
| 18-23 | 17.5-23.5 | 20.5 | 3 | 42 (=3+39) | |
| 24-29 | 23.5-29.5 | 26.5 | 6 | 48 (=6+42) | |
| 30-35 | 29.5-35.5 | 32.5 | 4 | 52 (=4+48) | |
| 36-41 | 35.5-41.5 | 38.5 | 2 | 54 (=2+52) | |
| 42-47 | 41.5-47.5 | 44.5 | 1 | 55 (=1+54) |
c.
Create a histogram for the given data on count of three-syllable words in advertising copy of magazine advertisements.
c.
Answer to Problem 20P
The frequency histogram for the data on count of three-syllable words in advertising copy of magazine advertisements is shown below:
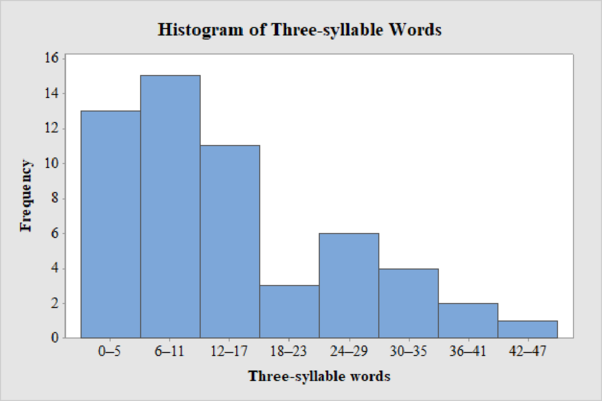
Explanation of Solution
Step-by-step procedure to draw the histogram using MINITAB software:
- Choose Graph > Bar Chart.
- From Bars represent, choose Values from a table.
- Under One column of values, choose Simple. Click OK.
- In Graph variables, enter the column of Frequency.
- In Categorical variables, enter the column of Three-syllable Words.
- Click OK.
Thus, the histogram for three-syllable word data is obtained.
d.
Construct a relative frequency histogram for the data on count of three-syllable words in advertising copy of magazine advertisements.
d.
Answer to Problem 20P
The relative frequency histogram for the data on count of three-syllable words in advertising copy of magazine advertisements is shown below:
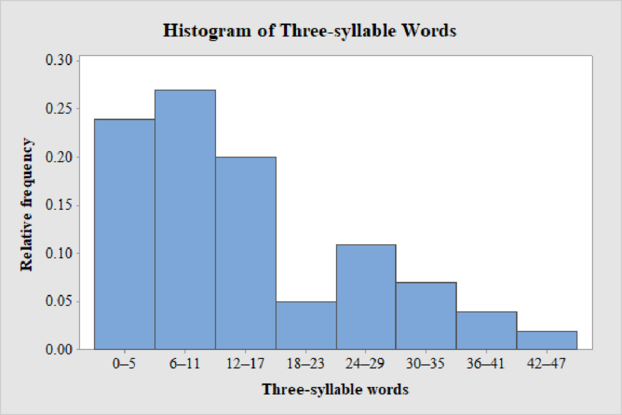
Explanation of Solution
Step-by-step procedure to draw the histogram using MINITAB software:
- Choose Graph > Bar Chart.
- From Bars represent, choose Values from a table.
- Under One column of values, choose Simple. Click OK.
- In Graph variables, enter the column of Relative frequency.
- In Categorical variables, enter the column of Three-syllable Words.
- Click OK.
Thus, the relative frequency histogram for three-syllable word data is obtained.
e.
Identify the shape of distribution: uniform, mound shaped, symmetric, bimodal, skewed left, or skewed right.
e.
Explanation of Solution
From the histogram, the distribution of count of three-syllable words in advertising copy of magazine advertisements is skewed to the right.
f.
Create an ogive curve for the given data on count of three-syllable words in advertising copy of magazine advertisements.
f.
Answer to Problem 20P
An ogive curve for the count of three-syllable words in advertising copy of magazine advertisements is shown below:
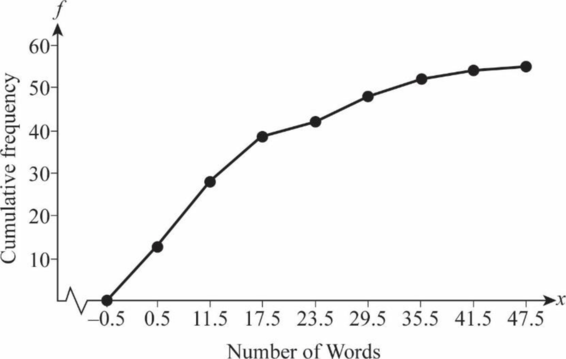
Explanation of Solution
Step-by-step procedure to draw the Ogive curve:
- Draw X axis with data values ranging from -0.5 to 47.5.
- Label the X axis as Number of Words.
- Draw Y axis with data values Cumulative frequency ranging from.0 to 60.
- Label the Y axis as Cumulative frequency.
- Plot the cumulative frequencies
- Join the points and draw an ogive curve.
Thus, an ogive curve for three-syllable word data is obtained.
g.
Identify the characteristics about the count of three-syllable words in advertising copy of magazine advertisements using the graphs.
g.
Explanation of Solution
The data values of count of three-syllable words in advertising copy of magazine advertisements fall within 0 and 43.
The
The central value of the data is approximately 11.5.
From the histogram, it can be observed that the data is skewed to the right and there are no unusual observations in the data as not even one data point is far from the overall bulk of data.
Want to see more full solutions like this?
Chapter 2 Solutions
WebAssign Printed Access Card for Brase/Brase's Understandable Statistics: Concepts and Methods, 12th Edition, Single-Term
- To: [Boss's Name] From: Nathaniel D Sain Date: 4/5/2025 Subject: Decision Analysis for Business Scenario Introduction to the Business Scenario Our delivery services business has been experiencing steady growth, leading to an increased demand for faster and more efficient deliveries. To meet this demand, we must decide on the best strategy to expand our fleet. The three possible alternatives under consideration are purchasing new delivery vehicles, leasing vehicles, or partnering with third-party drivers. The decision must account for various external factors, including fuel price fluctuations, demand stability, and competition growth, which we categorize as the states of nature. Each alternative presents unique advantages and challenges, and our goal is to select the most viable option using a structured decision-making approach. Alternatives and States of Nature The three alternatives for fleet expansion were chosen based on their cost implications, operational efficiency, and…arrow_forwardBusinessarrow_forwardWhy researchers are interested in describing measures of the center and measures of variation of a data set?arrow_forward
- WHAT IS THE SOLUTION?arrow_forwardThe following ordered data list shows the data speeds for cell phones used by a telephone company at an airport: A. Calculate the Measures of Central Tendency from the ungrouped data list. B. Group the data in an appropriate frequency table. C. Calculate the Measures of Central Tendency using the table in point B. 0.8 1.4 1.8 1.9 3.2 3.6 4.5 4.5 4.6 6.2 6.5 7.7 7.9 9.9 10.2 10.3 10.9 11.1 11.1 11.6 11.8 12.0 13.1 13.5 13.7 14.1 14.2 14.7 15.0 15.1 15.5 15.8 16.0 17.5 18.2 20.2 21.1 21.5 22.2 22.4 23.1 24.5 25.7 28.5 34.6 38.5 43.0 55.6 71.3 77.8arrow_forwardII Consider the following data matrix X: X1 X2 0.5 0.4 0.2 0.5 0.5 0.5 10.3 10 10.1 10.4 10.1 10.5 What will the resulting clusters be when using the k-Means method with k = 2. In your own words, explain why this result is indeed expected, i.e. why this clustering minimises the ESS map.arrow_forward
- why the answer is 3 and 10?arrow_forwardPS 9 Two films are shown on screen A and screen B at a cinema each evening. The numbers of people viewing the films on 12 consecutive evenings are shown in the back-to-back stem-and-leaf diagram. Screen A (12) Screen B (12) 8 037 34 7 6 4 0 534 74 1645678 92 71689 Key: 116|4 represents 61 viewers for A and 64 viewers for B A second stem-and-leaf diagram (with rows of the same width as the previous diagram) is drawn showing the total number of people viewing films at the cinema on each of these 12 evenings. Find the least and greatest possible number of rows that this second diagram could have. TIP On the evening when 30 people viewed films on screen A, there could have been as few as 37 or as many as 79 people viewing films on screen B.arrow_forwardQ.2.4 There are twelve (12) teams participating in a pub quiz. What is the probability of correctly predicting the top three teams at the end of the competition, in the correct order? Give your final answer as a fraction in its simplest form.arrow_forward
- The table below indicates the number of years of experience of a sample of employees who work on a particular production line and the corresponding number of units of a good that each employee produced last month. Years of Experience (x) Number of Goods (y) 11 63 5 57 1 48 4 54 5 45 3 51 Q.1.1 By completing the table below and then applying the relevant formulae, determine the line of best fit for this bivariate data set. Do NOT change the units for the variables. X y X2 xy Ex= Ey= EX2 EXY= Q.1.2 Estimate the number of units of the good that would have been produced last month by an employee with 8 years of experience. Q.1.3 Using your calculator, determine the coefficient of correlation for the data set. Interpret your answer. Q.1.4 Compute the coefficient of determination for the data set. Interpret your answer.arrow_forwardCan you answer this question for mearrow_forwardTechniques QUAT6221 2025 PT B... TM Tabudi Maphoru Activities Assessments Class Progress lIE Library • Help v The table below shows the prices (R) and quantities (kg) of rice, meat and potatoes items bought during 2013 and 2014: 2013 2014 P1Qo PoQo Q1Po P1Q1 Price Ро Quantity Qo Price P1 Quantity Q1 Rice 7 80 6 70 480 560 490 420 Meat 30 50 35 60 1 750 1 500 1 800 2 100 Potatoes 3 100 3 100 300 300 300 300 TOTAL 40 230 44 230 2 530 2 360 2 590 2 820 Instructions: 1 Corall dawn to tha bottom of thir ceraan urina se se tha haca nariad in archerca antarand cubmit Q Search ENG US 口X 2025/05arrow_forward
 Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt
Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt Functions and Change: A Modeling Approach to Coll...AlgebraISBN:9781337111348Author:Bruce Crauder, Benny Evans, Alan NoellPublisher:Cengage Learning
Functions and Change: A Modeling Approach to Coll...AlgebraISBN:9781337111348Author:Bruce Crauder, Benny Evans, Alan NoellPublisher:Cengage Learning



