Physics, Books a la Carte Edition (5th Edition)
5th Edition
ISBN: 9780134020853
Author: James S. Walker
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 21, Problem 107PP
Referring to Example 21-13 Suppose the three resistors in this circuit have the values R1 = 100.0 Ω, R2 = 200.0 Ω and R3 = 300.0 Ω, and the emf of the battery is 12.0 V. (The resistor numbers are given in the Interactive Figure.) (a) Find the potential difference across each resistor. (b) Find the current that flows through each resistor.
The circuit for this problem has three resistor connected to a battery. The lower two resistor are in series with one another, and in parallel with the upper resistor. The battery has an emf of 12.0 V.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
In the circuit diagram below, R1 = 5.00 Q, R2 = 10.0 Q, R3 = 15.0 N, C1 = 5.00 µF, C2 = 10.0 µF, and the ideal
battery has ɛ = 20.0 V. Assuming that the circuit is in the steady state, what is the total energy stored in the
two capacitors and find the current through each resistor.
%3D
%3D
%3D
Re
C2
Consider the three resistors R1 = 12 Ω, R2 = 44 Ω, and R3 = 88 Ω in the configuration shown in the figure. A potential difference ΔV = 3.5 V is applied between A and B.
A) Calculate the numerical value of the total resistance R of this circuit, in ohms.
B) Calculate the numerical value of the current I traveling from A to B, in amperes.
C) Calculate the numerical value of I2 traveling through the resistor R2, in amperes.
D) Calculate the numerical value of I3 traveling through the resistor R3, in amperes.
Problem 9:
A capacitor is charged with a total charge of q = 5.1E-05 C. The capacitor is wired in series with a resistor, R-8
Randomized Variables
q = 5.1 E-05 C
← Δ Part (a) Input an expression for the time constant, τ, of this circuit using the variables
provided and C for capacitance.
HOME
4 5 6
BACKS
CLEAR
Submit
Hint
I give up!
Hints: 1 -deduction per hint. Hints remaining:
Feedback:
deduction per feedback.
Part (b) What is the value of the time constant in s if the capacitor has capacitance of
1.0 μF?
Δ
Part (c) How long will it take the capacitor to discharge half of its charge in seconds?
Chapter 21 Solutions
Physics, Books a la Carte Edition (5th Edition)
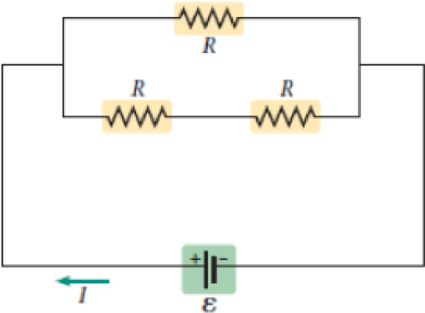
Ch. 21.1 - Enhance Your Understanding 1. The following...Ch. 21.2 - Enhance Your Understanding 2. If the voltage and...Ch. 21.3 - Enhance Your Understanding 3. In the following...Ch. 21.4 - The two circuits shown in Figure 21-17 have...Ch. 21.5 - Prob. 5EYUCh. 21.6 - Do two capacitors give a larger equivalent...Ch. 21.7 - Give a symbolic expression for the current that...Ch. 21 - Your body is composed of electric charges. Does it...Ch. 21 - Suppose you charge a comb by rubbing it through...Ch. 21 - An electron moving through a wire has an average...
Ch. 21 - Are car headlights connected in series or...Ch. 21 - Is it possible to connect a group of resistors of...Ch. 21 - What physical quantity do resistors connected in...Ch. 21 - What physical quantity do resistors connected in...Ch. 21 - Explain how electrical devices can begin operating...Ch. 21 - Explain the difference between resistivity and...Ch. 21 - Explain why birds can roost on high-voltage wires...Ch. 21 - Consider the circuit shown in Figure 21-36, in...Ch. 21 - A flashlight bulb carries a current of 0.38 A for...Ch. 21 - Predict/Calculate A car battery does 360 J of work...Ch. 21 - Highly sensitive ammeters can measure currents as...Ch. 21 - A television set connected to a 120-V outlet...Ch. 21 - BIO Pacemaker Batteries Pacemakers designed for...Ch. 21 - A conducting wire is quadrupled in length and...Ch. 21 - Figure 21-37 shows a plot of current versus...Ch. 21 - Predict/Explain Current-versus-voltage plots for...Ch. 21 - Prob. 9PCECh. 21 - When a potential difference of 12 V is applied to...Ch. 21 - Prob. 11PCECh. 21 - Prob. 12PCECh. 21 - Transcranial Direct-Current Stimulation In a tDCS...Ch. 21 - The four conducting cylinders shown in Figure...Ch. 21 - Predict/Calculate A bird lands on a bare copper...Ch. 21 - Prob. 16PCECh. 21 - Predict/Calculate BIO Current Through a Cell...Ch. 21 - Prob. 18PCECh. 21 - Prob. 19PCECh. 21 - BIO Resistance and Current in the Human Finger The...Ch. 21 - If a potential difference V is maintained between...Ch. 21 - Light A has four times the power rating of light B...Ch. 21 - Two lightbulbs operate on the same potential...Ch. 21 - Problems and Conceptual Exercises Section 21-3...Ch. 21 - A 65-V generator supplies 4.8 kW of power. How...Ch. 21 - A portable CD player operates with a current of 18...Ch. 21 - Find the power dissipated in a 22- electric heater...Ch. 21 - The current in a 120-V reading lamp is 2.6 A. If...Ch. 21 - Circuit A in a house has a voltage of 208 V and is...Ch. 21 - Predict/Calculate A 65-W lightbulb operates on a...Ch. 21 - Rating Car Batteries Car batteries are rated by...Ch. 21 - Predict/Explain A dozen identical lightbulbs are...Ch. 21 - A circuit consists of three resistors, R1 R2 R3,...Ch. 21 - Predict/Explain Two resistors are connected in...Ch. 21 - What is the minimum number of 88- resistors that...Ch. 21 - Find the equivalent resistance between points A...Ch. 21 - A 9.00-V battery is connected across the terminals...Ch. 21 - Holiday Lights In a string of holiday lights, 50...Ch. 21 - Your toaster has a power cord with a resistance of...Ch. 21 - Prob. 40PCECh. 21 - Predict/Calculate Three resistors, 11, 53 , and R,...Ch. 21 - A circuit consists of a battery connected to three...Ch. 21 - Predict/Calculate Three resistors, 22 , 67 , and...Ch. 21 - Prob. 44PCECh. 21 - The equivalent resistance between points A and B...Ch. 21 - Find the equivalent resistance between points A...Ch. 21 - How many 23-W lightbulbs can be connected in...Ch. 21 - The circuit in Figure 21-43 includes a battery...Ch. 21 - Predict/Calculate A 12-V battery is connected to...Ch. 21 - Predict/Calculate The terminals A and B in Figure...Ch. 21 - Predict/Calculate Suppose the battery in Figure...Ch. 21 - Predict/Calculate The current flowing through the...Ch. 21 - Predict/Calculate Four identical resistors are...Ch. 21 - Find the magnitude and direction (clockwise or...Ch. 21 - Predict/Calculate Suppose the polarity of the...Ch. 21 - Predict/Calculate It is given that point A in...Ch. 21 - Consider the circuit shown in Figure 21-47. Find...Ch. 21 - Suppose point A is grounded (V = 0) in Figure...Ch. 21 - Predict/Calculate (a) Find the current in each...Ch. 21 - Two batteries and three resistors are connected as...Ch. 21 - Two capacitors, C1 = C and C2 = 2C, are connected...Ch. 21 - Predict/Explain Two capacitors are connected in...Ch. 21 - Predict/Explain Two capacitors are connected in...Ch. 21 - A 252-F capacitor is connected in series with a...Ch. 21 - A 36-F capacitor is connected in parallel with an...Ch. 21 - Find the equivalent capacitance between points A...Ch. 21 - A 15-V battery is connected to three capacitors in...Ch. 21 - Three different circuits, each containing a switch...Ch. 21 - Terminals A and B in Figure 21-50 are connected to...Ch. 21 - Predict/Calculate You would like to add a second...Ch. 21 - Two capacitors, one 7.5 F and the other 15 F, are...Ch. 21 - The equivalent capacitance of the capacitors shown...Ch. 21 - With the switch in position A, the 11.2-F...Ch. 21 - The switch on an RC circuit is closed at t = 0....Ch. 21 - The capacitor in an RC circuit (R = 120 , C = 45...Ch. 21 - Three RC circuits have the emf, resistance, and...Ch. 21 - Consider an RC circuit with = 12.0 V, R = 195 ,...Ch. 21 - The resistor in an RC circuit has a resistance of...Ch. 21 - A flash unit for a camera has a capacitance of...Ch. 21 - Figure 21-54 shows a simplified circuit for a...Ch. 21 - Nerve Impulse Propagation The speed with which...Ch. 21 - Predict/Calculate Consider the RC circuit shown in...Ch. 21 - CE Consider the circuit shown in Figure 21-56, in...Ch. 21 - CE Predict/Explain (a) Referring to Problem 83 and...Ch. 21 - CE Consider the circuit shown in Figure 21-57, in...Ch. 21 - CE Predict/Explain (a) When the switch is closed...Ch. 21 - Suppose that points A and B in Figure 21-41 are...Ch. 21 - CE The circuit shown in Figure 21-58 shows a...Ch. 21 - CE The three circuits shown in Figure 21-59 have...Ch. 21 - Electrical Safety Codes For safety reasons,...Ch. 21 - A portable CD player uses a current of 7.5 mA at a...Ch. 21 - An electrical heating coil is immersed in 6.6 kg...Ch. 21 - Predict/Calculate Consider the circuit shown in...Ch. 21 - Prob. 94GPCh. 21 - BIO Pacemaker Pulses A pacemaker sends a pulse to...Ch. 21 - Three resistors (R,12R,2R) are connected to a...Ch. 21 - Predict/Calculate Suppose we connect a 12.0-V...Ch. 21 - National Electric Code In the United States, the...Ch. 21 - Solar Panel Power The current-versus-voltage plot...Ch. 21 - Predict/Calculate A 15.0-V battery is connected to...Ch. 21 - When two resistors, R1 and R2, are connected in...Ch. 21 - The circuit shown in Figure 21-62 is known as a...Ch. 21 - BIO Footwear Safety The American National...Ch. 21 - BIO Footwear Safety The American National...Ch. 21 - BIO Footwear Safety The American National...Ch. 21 - The standard specifies that footwear should be...Ch. 21 - Referring to Example 21-13 Suppose the three...Ch. 21 - Referring to Example 21-13 Suppose R1 = R2 = 225 ...Ch. 21 - Predict/Calculate Referring to Example 21-18...Ch. 21 - Predict/Calculate Referring to Example 21-18...
Additional Science Textbook Solutions
Find more solutions based on key concepts
If someone at the other end of a room smokes a cigarette, you may breathe in some smoke. The movement of smoke ...
Campbell Essential Biology with Physiology (5th Edition)
68. Correct any incorrect equations. If no reaction occurs, write NO REACTION.
a.
b.
c.
d.
Introductory Chemistry (6th Edition)
1. How many significant figures does each of the following numbers have?
a. 0.73 b. 7.30 c. 73 d. 0.073
Physics for Scientists and Engineers: A Strategic Approach, Vol. 1 (Chs 1-21) (4th Edition)
Which of the following factors would tend to increase membrane fluidity? A. a greater proportion of unsaturated...
Campbell Biology in Focus (2nd Edition)
What two body structures contain flexible elastic cartilage?
Anatomy & Physiology (6th Edition)
Fibrous connective tissue consists of ground substance and fibers that provide strength, support, and flexibili...
Human Biology: Concepts and Current Issues (8th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Similar questions
- The values of the components in a simple series RC circuit containing a switch (Fig. P21.53) are C = 1.00 F, R = 2.00 106 , and = 10.0 V. At the instant 10.0 s after the switch is closed, calculate (a) the charge on the capacitor, (b) the current in the resistor, (c) the rate at which energy is being stored in the capacitor, and (d) the rate at which energy is being delivered by the battery.arrow_forwardWhen resistors with different resistances are connected in parallel, which of the following must be the same for each resistor? Choose all correct answers, (a) potential difference (b) current (c) power delivered (d) charge entering each resistor in a given time interval (e) none of those answersarrow_forwardA capacitor with initial charge Q0 is connected across a resistor R at time t = 0. The separation between the plates of the capacitor changes as d = d0/(1 + t) for 0 t 1 s. Find an expression for the voltage drop across the capacitor as a function of time.arrow_forward
- Electric current I enters a node with three resistors connected in parallel (Fig. CQ18.5). Which one of the following is correct? (a) I1 = I and I2 = I3 = 0. (b) I2 I1 and I2 I3. (c) V1 V2 V3 (d) I1 I2 I3 0. Figure CQ18.5arrow_forwardDraw two graphs of charge versus time on a capacitor. Draw one for charging an initially uncharged capacitor in series with a resistor, as in the circuit in Figure 21.38, starting from t = 0. Draw the other for discharging a capacitor through a resistor, as in the circuit in Figure 21.39, starting at t = 0, with an initial charge Q0. Show at least two intervals of t.arrow_forwardWhen resistors with different resistances are connected in series, which of the following must be the same for each resistor? Choose all correct answers. (a) potential difference (b) current (c) power delivered (d) charge entering each resistor in a given time interval (e) none of those answersarrow_forward
- An automobile starter motor has an equivalent resistance of 0.0500 and is supplied by a 12.0-V battery with a 0.0100- internal resistance, (a) What is thecurrent to the motor? (b) What voltage is applied to it? (c) What power is supplied to the motor? (d) Repeat these calculations for when the battery connections are corroded and add 0.0900 to the circuit. (Significant problems are caused by even small amounts of unwanted resistance in low-voltage, high-current applications.)arrow_forwardThe terminals of a battery are connected across two resistors in series. The resistances of the resistors are not the same. Which of the following statements are correct? Choose all that are correct. (a) The resistor with the smaller resistance carries more current than the other resistor. (b) The resistor with the larger resistance carries less current than the other resistor. (c) The current in each resistor is the same. (d) The potential difference across each resistor is the same. (e) The potential difference is greatest across the resistor closest to the positive terminal.arrow_forwardThe terminals of a battery are connected across two resistors in parallel. The resistances of the resistors are not the same. Which of the following statements is correct? Choose all that are correct. (a) The resistor with the larger resistance carries more current than the other resistor. (b) The resistor with the larger resistance carries less current than the other resistor. (c) The potential difference across each resistor is the same. (d) The potential difference across the larger resistor is greater than the potential difference across the smaller resistor. (e) The potential difference is greater across the resistor closer to the battery.arrow_forward
- Power P0 = I0 V0 is delivered to a resistor of resistance R0. If the resistance is doubled (Rnew = 2R0) while the voltage is adjusted such that the current is constant, what are the ratios (a) Pnew/P0 and (b) Vnew/V0? If, instead, the resistance is held constant while Pnew = 2P0, what are the ratios (c) Vnew/V0, and (d) Inew/I0?arrow_forwardProblem 8: Consider the following figure. r = 2.0 Ω E = 18 V r = 1.0 Ω E = 12 V R = 4.8 Ω a) Calculate the current flowing in the circuit. b) Determine the terminal voltage of each battery in the figure.arrow_forwardThe circuit of the figure shows a capacitor, two ideal batteries, two resistors, and a switch S. Initially S has been open for a long time. If it is then closed for a long time, what is the change in the charge on the capacitor? Assume C = 41 μF, 81 = 4.1 V, 82 = 5.3 V, R₁ = 0.520, and R₂ = 0.45 0. Number ap Units R₁ C R₂ wwwarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Principles of Physics: A Calculus-Based Text
Physics
ISBN:9781133104261
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...
Physics
ISBN:9781305116399
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
College Physics
Physics
ISBN:9781305952300
Author:Raymond A. Serway, Chris Vuille
Publisher:Cengage Learning
College Physics
Physics
ISBN:9781285737027
Author:Raymond A. Serway, Chris Vuille
Publisher:Cengage Learning
College Physics
Physics
ISBN:9781938168000
Author:Paul Peter Urone, Roger Hinrichs
Publisher:OpenStax College
Physics for Scientists and Engineers: Foundations...
Physics
ISBN:9781133939146
Author:Katz, Debora M.
Publisher:Cengage Learning
How To Solve Any Resistors In Series and Parallel Combination Circuit Problems in Physics; Author: The Organic Chemistry Tutor;https://www.youtube.com/watch?v=eFlJy0cPbsY;License: Standard YouTube License, CC-BY