
Concept explainers
As early as 650 BC, mathematicians have been composing magic squares, a sequence of n numbers arranged in a square such that all rows, columns, and diagonals sum to the same constant. Used in China, India, and Arab countries for centuries, artist Albrecht Durer’s engraving Melencolia I (year: 1514) is considered the first time a magic square appears in European art. Each row, column, and diagonal of Dürer’s magic square sums to 34. In addition, each quadrant, the center four squares, and the corner squares all sum to 34. The following is an example of a magic square:
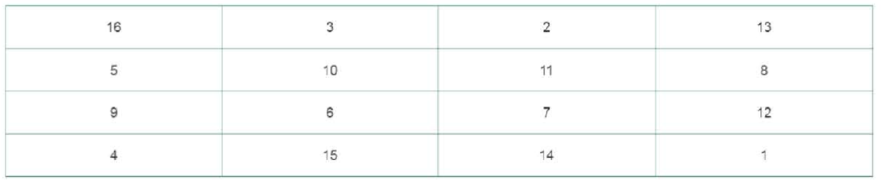
Write a program to determine if a series of numbers is indeed a 4 × 4 magic square. Your program should complete the following steps, in this order
- a. Ask the user to enter the proposed magic square in a single input statement (e.g., [1 2 3 4; 5 6 7 8; 9 10 11 12; 13 14 15 16]—note this example is a 4 × 4 matrix, but NOT a magic square). You may assume the user will enter whole numbers; they will not enter either decimal values or text.
- b. Check that all values are positive; ** for-loop or nested for-loop required in the solution. If one or more of the values in the matrix are negative or zero, issue a statement to the command window informing the user of the mistake and ask the user to enter another matrix. This check should be repeated until the user enters a matrix with positive values. This check should work even if the user does not enter a 4 × 4 matrix; it should work regardless of the size of matrix entered.
- c. Check for an arrangement of 4 × 4 If the matrix is not a 4 × 4, issue a statement to the command window informing the user of the mistake, and ask the user to enter another matrix. This check should be repeated until the user enters a 4 × 4 matrix. You may assume the reentered matrix contains only positive values; you do not need to recheck the new matrix for positive values, only for matrix dimensions.
- d. Determine if the matrix is a form of a magic square. The minimum requirement to be classified as a magic square is each row and column sums to the same value. ** for-loop or nested for-loop required in the solution. If this criterion is not met, issue a statement to the command window informing the user they have not entered a magic square and ask the user if they wish to try another magic square. This question can be posed using either a text answer entered by the user (Yes, No) or by using a menu. If the user chooses to run the program again, the entire program starting with step (a) should begin again.
- e. Determine the classification of the magic square using the following requirements:
- 1. If each row and column sums to the same value, the magic square is classified as semi-magic; the summation value is ca led the magic constant. **for-loop or nested for-loop required in the solution.
- 2. If, in addition to criterion 1, each diagonal sums to the same value, the magic square is classified as normal; **for-loop or nested for-loop required in the solution. The use of built-in functions such as diag, flipir, rot90, trace or similar built-in functions is forbidden.
- 3. If, in addition to 1 and 2, the largest value in the magic square is equal to 16, the magic square is classified as perfect.
Format your magic square classification similar to the format shown below. You may choose to format your table differently, but each classification should contain a Yes or No next to each magic square category.
The magic constant for your magic square is 24. The classification for your magic square:
| Semi-magic | Normal | Perfect |
| Yes | Yes | Yes |
After this table appears, ask users if they wish to try another magic square following the instructions given earlier. A few test cases for you to consider:
- Albrecht Dürer magic square: [16, 3, 2, 13; 5, 10, 11, 8; 9, 6, 7, 12, 4, 15, 14, 1];
- Chautisa Yantra magic square: [7, 12, 1, 14, 2, 13, 8, 11; 16, 3, 10, 5; 9, 6, 15, 4];
- Sangrada Familia church, Barcelona magic square: [1, 14, 14, 4; 11, 7, 6, 9; 8, 10, 10, 5; 13, 2, 3, 15].
- Random magic square: [80, 15, 10, 65; 25, 50, 55, 40; 45, 30, 35, 60; 20, 75, 70, 5];
- Steve Wozniak’s magic square: [8, 11, 22, 1; 21, 2, 7, 12; 3, 24, 9, 6; 10, 5, 4, 23]
Want to see the full answer?
Check out a sample textbook solution
Chapter 20 Solutions
Thinking Like an Engineer
- Copyright 2013 Pearson Education, publishing as Prentice Hall 2. Determine the force that the jaws J of the metal cutters exert on the smooth cable C if 100-N forces are applied to the handles. The jaws are pinned at E and A, and D and B. There is also a pin at F. E 400 mm 15° D B 30 mm² 80 mm/ 20 mm 15° $15° 20 mm 400 mm 15° 100 N 100 N 15°arrow_forwardDraw for it make a match which directionarrow_forwardQ.1) Block A is connected to block B by a pulley system as shown. The weights of blocks A and B are 100 lbs and 70 lbs, respectively. Assume negligible friction between the rope and all pulleys as well as between block B and the incline and neglect the mass of all pulleys and cables. Determine the angle 0 required to keep the system in equilibrium. (At least two FBDs must be drawn for full credit) B Ꮎ 000arrow_forward
- pls solvearrow_forward+1. 0,63 fin r= 0.051 P The stepped rod in sketch is subjected to a tensile force that varies between 4000 and 7000 lb. The rod has a machined surface finish everywhere except the shoulder area, where a grinding operation has been performed to improve the fatigue resistance of the rod. Using a 99% probability of survival, determine the safety factor for infinite life if the rod is made of AISI 1080 steel, quenched and tempered at 800°c Use the Goodman line. Does the part fail at the fillet? Explainarrow_forwardSolve this problem and show all of the workarrow_forward
- I need drawing solution,draw each one by one no Aiarrow_forwardQu. 17 Compute linear density values for [100] for silver (Ag). Express your answer in nm''. . Round off the answer to three significant figures. Qu. 18 Compute linear density value for [111] direction for silver (Ag). Express your answer in nm'. Round off the answer to three significant figures. Qu. 19 Compute planar density value for (100) plane for chromium (Cr). Express your answer in nm?. Round off the answer to two significant figures. Qu. 20 Compute planar density value for (110) plane for chromium (Cr). Express your answer in nm ≥ to four significant figures. show all work please in material engineeringarrow_forward3-142arrow_forward
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





