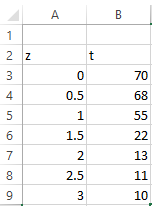
Given Information:
The table is given as,
| Depth, m |
0 |
0.5 |
1.0 |
1.5 |
2.0 |
2.5 |
3.0 |
| Temperature, Celsius |
70 |
68 |
55 |
22 |
13 |
11 |
10 |
The provided graph shows the relationship between depth and temperature as,
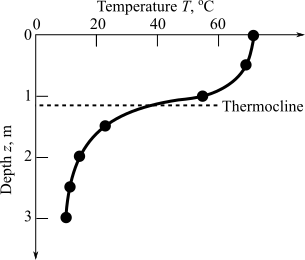
Calculation:
Consider the Fourier’s law,
J=−kdTdz …… (1)
The value of k=0.02cal/s⋅cm⋅°C is given. Therefore, it is required to calculate dTdz.
From the graph, this can be interpreted that curve has zero slope at z=1.2 m.
Since, the cubic spline fit is required, so this problem can be solved by the Excel VBA(Visual Basic for applications). The steps are,
Step 1. Insert the data in excel as shown below,
Step 2. Press ALT+F11 and write the code as shown below,
OptionExplicit
SubSplines()
'nop and u is declared as integer type variable.
Dim u AsInteger,nopAsInteger
'arrayArr_x, Arr_y, fder, js, fder, sder and ms is declare as double type variable.
DimArr_x(100)AsDouble,Arr_y(100)AsDouble,jsAsDouble,msAsDouble
DimfderAsDouble,sderAsDouble
'rp is declared as variant.
DimrpAsVariant
'5th row is selected.
Range("a5").Select
'store the value of 5th row in nop.
nop=ActiveCell.Row
'last shell of excel is selected.
Selection.End(xlDown).Select
'store the value of last shell in nop.
nop=ActiveCell.Row-nop
'5th row is selected.
Range("a5").Select
'for loop is run uptonop.
For u =0Tonop
'store the value in array x.
Arr_x(u)=ActiveCell.Value
ActiveCell.Offset(0,1).Select
'store the value in array y.
Arr_y(u)=ActiveCell.Value
ActiveCell.Offset(1,-1).Select
'u value is increamented.
Next u
'5th row of column is selected.
Range("c5").Select
Range("c5:d1005").ClearContents
'for loop is run uptonop.
For u =0Tonop
'spline function is call.
CallSpline(Arr_x(),Arr_y(),nop,Arr_x(u),ms,fder,sder)
'first derivative value is stored.
ActiveCell.Value=fder
ActiveCell.Offset(0,1).Select
'second derivative value is stored.
ActiveCell.Value=sder
ActiveCell.Offset(1,-1).Select
'value is incremented by 1.
Next u
Do
'thismsg is asked from user.
rp=MsgBox("Do you want to interpolate?",vbYesNo)
'if condition is to check the value.
Ifrp=vbNoThenExitDo
js=InputBox("z = ")
'Spline function is called
CallSpline(Arr_x(),Arr_y(),nop,js,ms,fder,sder)
MsgBox"For z = "&js&Chr(13)&"T = "&ms&Chr(13)& _
"dT/dz = "&fder&Chr(13)&"d2T/dz2 = "&sder
'loop is ended.
Loop
'function is ended.
EndSub
'spline function is defined.
SubSpline(Arr_x,Arr_y,nop,js,ms,fder,sder)
'arraye,f,g,r and d2x is declared as double type
Dim e(100)AsDouble, f(100)AsDouble, g(100)AsDouble, r(100)AsDouble, d2x(100)AsDouble
'tridiag function is called.
CallTridiag(Arr_x,Arr_y,nop, e, f, g, r)
'decomp function is called.
CallDecomp(e(), f(), g(),nop-1)
'Substite function is called.
CallSubstit(e(), f(), g(), r(),nop-1, d2x())
'interpolation function is abbreviated as interpol.
CallInterpol(Arr_x,Arr_y,nop, d2x(),js,ms,fder,sder)
'function is ended.
EndSub
'Tridiag definition is given.
SubTridiag(Arr_x,Arr_y,nop, e, f, g, r)
'u is declare the variable as integer type.
Dim u AsInteger
'f(1),g(1) and r(1)value is calculated.
f(1)=2*(Arr_x(2)-Arr_x(0))
g(1)=Arr_x(2)-Arr_x(1)
r(1)=6/(Arr_x(2)-Arr_x(1))*(Arr_y(2)-Arr_y(1))
r(1)= r(1)+6/(Arr_x(1)-Arr_x(0))*(Arr_y(0)-Arr_y(1))
'for loop is run upto nop-2.
For u =2Tonop-2
e(u)=Arr_x(u)-Arr_x(u -1)
f(u)=2*(Arr_x(u +1)-Arr_x(u -1))
g(u)=Arr_x(u +1)-Arr_x(u)
r(u)=6/(Arr_x(u +1)-Arr_x(u))*(Arr_y(u +1)-Arr_y(u))
r(u)= r(u)+6/(Arr_x(u)-Arr_x(u -1))*(Arr_y(u -1)-Arr_y(u))
'value is incremented by 1.
Next u
'e(nop-1)value is calculated.
e(nop-1)=Arr_x(nop-1)-Arr_x(nop-2)
'f(nop-1)value is calculated.
f(nop-1)=2*(Arr_x(nop)-Arr_x(nop-2))
'r(nop-1)value is calculated.
r(nop-1)=6/(Arr_x(nop)-Arr_x(nop-1))*(Arr_y(nop)-Arr_y(nop-1))
r(nop-1)= r(nop-1)+6/(Arr_x(nop-1)-Arr_x(nop-2))*(Arr_y(nop-2)-Arr_y(nop-1))
'function is ended.
EndSub
'Interpol is defined.
SubInterpol(Arr_x,Arr_y,nop, d2x,js,ms,fder,sder)
'u and flag is declared the variable as integer type
Dim u AsInteger, flag AsInteger
'variable C1,C2,C3 and C4 is declared as double type
Dim C1 AsDouble, C2 AsDouble, C3 AsDouble, C4 AsDouble
'variable T1,T2,T3 and T4 is declared as double type
Dim T1 AsDouble, T2 AsDouble, T3 AsDouble, T4 AsDouble
'flag and u is initialised as 0.
flag=0
u =1
Do
'if statement is to check the condition.
Ifjs>=Arr_x(u -1)Andjs<=Arr_x(u)Then
'C1 is calculated.
C1 =d2x(u -1)/6/(Arr_x(u)-Arr_x(u -1))
'C2 is calculated.
C2 =d2x(u)/6/(Arr_x(u)-Arr_x(u -1))
'C3 is calculated.
C3 =Arr_y(u -1)/(Arr_x(u)-Arr_x(u -1))- d2x(u -1)*(Arr_x(u)-Arr_x(u -1))/6
'C4 is calculated.
C4 =Arr_y(u)/(Arr_x(u)-Arr_x(u -1))- d2x(u)*(Arr_x(u)-Arr_x(u -1))/6
'T1 is calculated.
T1 = C1 *(Arr_x(u)-js)^3
'T2 is calculated.
T2 = C2 *(js-Arr_x(u -1))^3
'T3 is calculated.
T3 = C3 *(Arr_x(u)-js)
'T4 is calculated.
T4 = C4 *(js-Arr_x(u -1))
'ms is calculated.
ms= T1 + T2 + T3 + T4
'T1 is calculated.
T1 =-3* C1 *(Arr_x(u)-js)^2
'T2 is calculated.
T2 =3* C2 *(js-Arr_x(u -1))^2
'T3 is calculated.
T3 =-C3
'T4 is calculated.
T4 = C4
'fder value is calculated.
fder= T1 + T2 + T3 + T4
'T1 and T2 is calculated.
T1 =6* C1 *(Arr_x(u)-js)
T2 =6* C2 *(js-Arr_x(u -1))
'second derivative sder is calculated.
sder= T1 + T2
'flag is equal to 1
flag=1
Else
u = u +1
EndIf
'if statement is to check the calculated value.
If u =nop+1Or flag =1ThenExitDo
Loop
'flag is checked
If flag =0Then
'if condition is fulfil then output the msg.
MsgBox"outside range"
'loop is ended.
End
'end statement.
EndIf
'function is ended.
EndSub
'Decomp function definition is given.
SubDecomp(e, f, g,nop)
'k is declared as integer
Dim k AsInteger
'for loop is run uptonop.
For k =2Tonop
e(k)= e(k)/ f(k -1)
f(k)= f(k)- e(k)* g(k -1)
'k is increased by 1.
Next k
'function is ended.
EndSub
'substit definition is given.
SubSubstit(e, f, g, r,nop,Arr_x)
'k is declared as integer type.
Dim k AsInteger
'for loop is run uptonop.
For k =2Tonop
r(k)= r(k)- e(k)* r(k -1)
'k is increased.
Next k
'Arr_x(nop)value is calculated.
Arr_x(nop)= r(nop)/ f(nop)
'for loop is run uptoArr_x(k)
For k =nop-1To1Step-1
Arr_x(k)=(r(k)- g(k)*Arr_x(k +1))/ f(k)
' k is increased by 1
Next k
' function is ended.
EndSub
PrivateSubWorksheet_SelectionChange(ByVal Target As Range)
EndSub
Step 3. Press RUN then this dialog box appears.
Step 4. Enter the value of z.

Step 5. This output will appear.
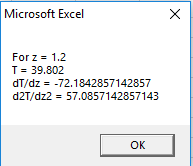
Thus, the value of dTdz is −72.18. Substitute this value in equation (1),
J=−0.02(−72.18)100=0.014436cal/cm2s
Hence, the value of thermocline depth and the flux across the interface is −72.18°C/m and0.014436cal/cm2s respectively.







 Functions and Change: A Modeling Approach to Coll...AlgebraISBN:9781337111348Author:Bruce Crauder, Benny Evans, Alan NoellPublisher:Cengage Learning
Functions and Change: A Modeling Approach to Coll...AlgebraISBN:9781337111348Author:Bruce Crauder, Benny Evans, Alan NoellPublisher:Cengage Learning Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill



