Chapter 2, Problem 9PP

(Civil eng.) The maximum load that can be placed at the end of a symmetrical wooden beam, such as the rectangular beam shown in Figure 2.20, can be calculated as the following:

$L=\frac{S\times 1}{d\times c}$

L is the maximum weight in lbs of the load placed on the beam.

S is the stress in lbs/in².

I is the beam’s rectangular moment of inertia in units of in4.

d is the distance in inches that the load is placed from the fixed end of the beam (the

“moment arm”).

c is one-half the height in inches of the symmetrical beam.

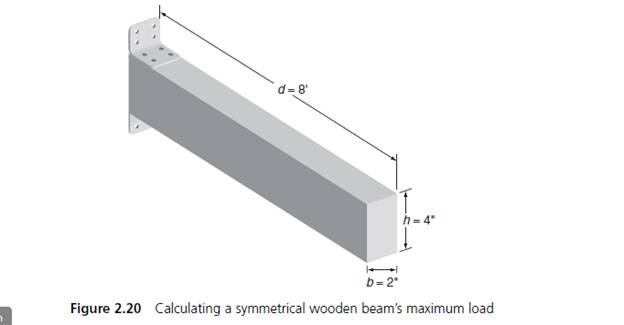
For a 2” × 4” wooden beam, the rectangular moment of inertia is given by this formula:

$I=\frac{base\times heigh{t}^3=}{12}=\frac{2\times 4^3}{12}={10.67}^4$

$c=\mathrm{½}\left(4in\right)=2in$

a. Using this information, design, write, compile, and run a C++ program that computes the

maximum load in lbs that can be placed at the end of an 8-foot $2”\times 4”$ wooden beam so that

the stress on the fixed end is $3000lb/i{n}^2.$

b. Use the program developed in Exercise 9a to determine the maximum load in lbs that can be placed at the end of a 3” × 6” wooden beam so that the stress on the fixed end is $3000lb/i{n}^2.$