C++ for Engineers and Scientists
4th Edition
ISBN: 9781133187844
Author: Bronson, Gary J.
Publisher: Course Technology Ptr
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 2, Problem 11PP
(
r is the radius of the cylindrical rod in inches.
d is the length of the crank arm in inches.
P is the weight placed on the pedal in lbs.
S is the stress in lbs/in2.
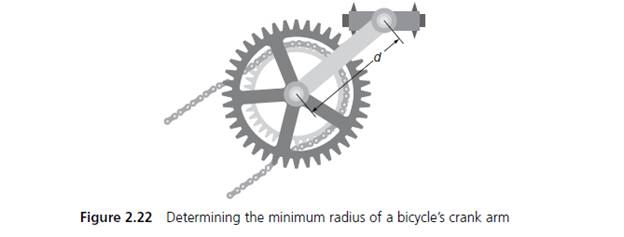
Using this information, design, write, compile, and run a C++
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Simulate on a vertical time axis (with events labeled with the senders names A-D) the contention period of FOUR equally distanced Ethernet stations that all attempt to transmit at T=0 a minimally sized frame, in the style of the binary Exponential Backoff Algorithm. Assume that time is measured in slot times, and that exactly one slot time is needed to detect a collision (so that if two stations transmit at T=1 and collide, and one of them chooses a backoff time k=0, then that station will transmit again at T=2).
Use as coin flip (source of randomness) an ID written in binary.
use the bits in order from the least significant to the most significant. If for a given coin throw you need k bits, use the least significant ID bit extracted in the corresponding group of bits, as the least significant bit of the coin thrown.
Start be writing the ID, which is 904012207
As example of the expected answer format,
with the random sequence R: 100101010101001011001010 01 01011 10010 1010 1010 010…
Big State University
The Big State University course catalog reads as follows: "To enroll in MIS 260, which is an advanced
course, a student must complete two prerequisites: MIS 120 and MIS 222. A student who completes
either one of these prerequisites and obtains the instructor's permission, however, will be allowed to
take MIS 260."
Tasks
1. Create a decision table that describes the Big State University course catalog regarding eligibility for
MIS 260. Show all possible rules.
2. Simplify the table you just created. Describe the results.
3. Draw a simplified decision tree to represent the Big State University catalog. Describe the results.
4. Why might you use a decision tree rather than a decision table?
What is the ALU result if the 4-bit ALU Control signal is 0100? What happens if the ALU Control signal is 0101?
Chapter 2 Solutions
C++ for Engineers and Scientists
Ch. 2.1 - (Practice) State whether the following are valid...Ch. 2.1 - Prob. 2ECh. 2.1 - Prob. 3ECh. 2.1 - (Practice) Determine names for functions that do...Ch. 2.1 - (Program) a. Using cout, write a C++ program that...Ch. 2.1 - (Program) a. Write a C++ program to display the...Ch. 2.1 - (Program) a. How many cout statements would you...Ch. 2.1 - (Program) a. Assuming your compiler isn’t case...Ch. 2.1 - (Practice) You’re given the task of wiring and...Ch. 2.1 - (Practice) You’re given the job of preparing a...
Ch. 2.1 - (Practice) You’re a sophomore in college and are...Ch. 2.1 - (Practice) You’re given the job of planting a...Ch. 2.1 - (Practice) You’re responsible for planning and...Ch. 2.1 - (Data processing) a. A national medical testing...Ch. 2.2 - (Debug) a. Will the following program work?...Ch. 2.2 - (Modify) Rewrite the following programs to conform...Ch. 2.2 - (For thought) a. When used in a message, the...Ch. 2.2 - (For thought) a. A token of a computer language is...Ch. 2.3 - (Practice) Determine data types appropriate for...Ch. 2.3 - (Practice) Compile and run Program 2.5.Ch. 2.3 - Prob. 3ECh. 2.3 - (Practice) Show how the name KINGSLEY is stored in...Ch. 2.3 - Prob. 5ECh. 2.3 - Prob. 6ECh. 2.3 - Prob. 7ECh. 2.3 - (For thought) Although you have concentrated on...Ch. 2.3 - (Practice) Although the total number of bytes...Ch. 2.4 - (Practice) For the following correct algebraic...Ch. 2.4 - (Practice) Determine the values of the following...Ch. 2.4 - (Practice) Determine the value of the following...Ch. 2.4 - (Practice) Evaluate the following mixed-mode...Ch. 2.4 - Prob. 5ECh. 2.4 - Prob. 6ECh. 2.4 - Prob. 7ECh. 2.4 - Prob. 8ECh. 2.4 - Prob. 9ECh. 2.4 - (Program) Write a C++ program that displays the...Ch. 2.4 - Prob. 11ECh. 2.5 - (Practice) State whether the following variable...Ch. 2.5 - Prob. 2ECh. 2.5 - (Practice) a. Write a declaration statement to...Ch. 2.5 - Prob. 4ECh. 2.5 - Prob. 5ECh. 2.5 - Prob. 6ECh. 2.5 - Prob. 7ECh. 2.5 - Prob. 8ECh. 2.5 - (Practice) a. Using Figure 2.14 and assuming the...Ch. 2.5 - Prob. 10ECh. 2.5 - Prob. 11ECh. 2.6 - (Modify) a. Modify Program 2.11 to calculate the...Ch. 2.6 - (Modify) a. Modify Program 2.11 to determine the...Ch. 2.6 - Prob. 3ECh. 2.6 - Prob. 4ECh. 2.6 - (Conversion) a. Design, write, compile, and run a...Ch. 2.6 - (Hydraulics) a. Write, compile, and run a C++...Ch. 2.6 - (Thermodynamics) a. Design, write, compile, and...Ch. 2.6 - Prob. 8ECh. 2 - (General math) a. Design, write, compile, and run...Ch. 2 - (General math) a. Design, write, compile, and run...Ch. 2 - (Physics) a. Design, write, compile, and run a C++...Ch. 2 - Prob. 4PPCh. 2 - (Hydraulics) a. Design, write, compile, and run a...Ch. 2 - Prob. 6PPCh. 2 - (Physics) a. The weight of an object on Earth is a...Ch. 2 - (Modify) a. Modify the program you wrote for...Ch. 2 - (Civil eng.) The maximum load that can be placed...Ch. 2 - (Civil eng.) Modify the program written for...Ch. 2 - (Mechanical eng.) The minimum radius required for...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, computer-science and related others by exploring similar questions and additional content below.Similar questions
- #include int main (void) { int i, *p, count } p = &count; = 10%; for (i = 5; i >= 0; i--) { count++; (*p) ++; } printf("count return 0; = %d, Have a wonderful day.\n", count); 1. [20 pts] What is the output of the program? Please explain why. 2. [15 pts] What is the gdb command to set a breakpoint in line 6 (p = &count;)? 3. [15 pts] Explain in your own words how the [break. need to use such command? ... if expr] command works. When might youarrow_forwardPlease run and debug the following program and answer the questions.arrow_forward(OnlineGDB) #include <stdio.h>int main(void) {int a;char *s;int v0 = 4, v1 = 5, v2 = 6, v3 = 1, v4 = 2;printf("Exercise 1:\n====================\n");switch(v0) {case 0: printf("Hello October\n"); break;case 1: printf("Go Kean!\n"); break;case 2: printf("Academic Building Center \n"); break;case 3: printf("UNION \n"); break;case 4: printf("Go ");case 5: printf("Kean! \n");default: printf("Have a great semester! \n"); break;}for(a=5; a<v1; a++) {printf("Kean");}printf("\n");if (v2 == 6) {s = "Go";}else {s = "Hello";}if(v3 != v4) {printf("%s Kean!\n",s);} else {printf("%s Computer Science!\n",s);}return 0;} Assume the following codes are added between line 36 (}) and line 38 (return 0;) v0>0 ? ++v1, ++v2 : --v3; Please give the values of v0, v1, v2, v3, and v4 after this line and explain the reason. You can test the program to verify your answer if you like.arrow_forward
- #include <stdio.h>int main(void) {int a;char *s;int v0 = 4, v1 = 5, v2 = 6, v3 = 1, v4 = 2;printf("Exercise 1:\n====================\n");switch(v0) {case 0: printf("Hello October\n"); break;case 1: printf("Go Kean!\n"); break;case 2: printf("Academic Building Center \n"); break;case 3: printf("UNION \n"); break;case 4: printf("Go ");case 5: printf("Kean! \n");default: printf("Have a great semester! \n"); break;}for(a=5; a<v1; a++) {printf("Kean");}printf("\n");if (v2 == 6) {s = "Go";}else {s = "Hello";}if(v3 != v4) {printf("%s Kean!\n",s);} else {printf("%s Computer Science!\n",s);}return 0;} Output: Exercise 1:====================Go Kean! Have a great semester! Go Kean! Please only modify the initial value of v0, v1, v2, v3 and v4 to get the following output. Youneed to show your program output (in the screenshot) and submit the code that youmodified.Exercise 1:====================Hello OctoberKeanHello Computer Science!arrow_forward(OnlineGDB) 1. Please read and run the following code and answer the questions.#include <stdio.h>int main(void) {int a;char *s;int v0 = 4, v1 = 5, v2 = 6, v3 = 1, v4 = 2;printf("Exercise 1:\n====================\n");switch(v0) {case 0: printf("Hello October\n"); break;case 1: printf("Go Kean!\n"); break;case 2: printf("Academic Building Center \n"); break;case 3: printf("UNION \n"); break;case 4: printf("Go ");case 5: printf("Kean! \n");default: printf("Have a great semester! \n"); break;}for(a=5; a<v1; a++) {printf("Kean");}printf("\n");if (v2 == 6) {s = "Go";}else {s = "Hello";}if(v3 != v4) {printf("%s Kean!\n",s);} else {printf("%s Computer Science!\n",s);}return 0;} What is the output of the program? Please explain why.arrow_forward1.[30 pts] Answer the following questions: a. [10 pts] Write a Boolean equation in sum-of-products canonical form for the truth table shown below: A B C Y 0 0 0 1 0 0 1 0 0 1 0 0 0 1 1 0 1 0 0 1 1 0 1 0 1 1 0 1 1 1 1 0 a. [10 pts] Minimize the Boolean equation you obtained in (a). b. [10 pts] Implement, using Logisim, the simplified logic circuit. Include an image of the circuitarrow_forward
- In the past, encryption and decryption were mostly done by substitution and permutation of letters in a text message. study those classic cryptographic schemes Then, develop an automatic cipher using Javascript The cipher should be able to perform the following tasks: generate keys encrypt a given plaintext message with a key selected from the list of keys generated decrypt a given ciphertext message with a known cipher keyarrow_forwardList reasons why teachers should and shouldn’t be replaced by computers? State your response in a descriptive context. Provide five references from the with internet with your answers.arrow_forwardThe attached picture shows the RTCAPI memory mapped register which has the address 0x180. 1) Program the MCU's registers so that a) SIRC is the clock source b) the clock is divided by 16K c) the clock is enabled d) load is enabledarrow_forward
- What is the ALU result if the 4-bit ALU Control signal is 0100? What happens if the ALU Control signal is 0101?arrow_forwardIn the past, encryption and decryption were mostly done by substitution and permutation of letters in a text message. study those classic cryptographic schemes Then, develop an automatic cipher using a programming language of your choice. The cipher should be able to perform the following tasks: generate keys encrypt a given plaintext message with a key selected from the list of keys generated decrypt a given ciphertext message with a known cipher keyarrow_forwardCase Study Instructions: Offshore Wind Energy in the North Sea For this case study, students will analyze the institutional challenges and social rules surrounding offshore wind energy development in the Dutch North Sea, as explored in the case study from the textbook (pages 44-46). Additional resources in this week’s learning module will provide further perspectives on the impact of wind energy on different stakeholders. Students should refer to the syllabus for specific guidelines regarding length, format, and content requirements. Reflection Questions to Consider: What are the key institutional challenges in implementing offshore wind energy in the North Sea? How do formal and informal social rules shape the use of this shared space? What conflicts arise between different stakeholders (e.g., fishermen, naval transport, military, and wind energy developers)? How can policymakers balance economic, environmental, and social considerations when allocating space for wind energy?…arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
C++ for Engineers and ScientistsComputer ScienceISBN:9781133187844Author:Bronson, Gary J.Publisher:Course Technology Ptr
Operations Research : Applications and AlgorithmsComputer ScienceISBN:9780534380588Author:Wayne L. WinstonPublisher:Brooks Cole
C++ Programming: From Problem Analysis to Program...Computer ScienceISBN:9781337102087Author:D. S. MalikPublisher:Cengage Learning
C++ for Engineers and Scientists
Computer Science
ISBN:9781133187844
Author:Bronson, Gary J.
Publisher:Course Technology Ptr
Operations Research : Applications and Algorithms
Computer Science
ISBN:9780534380588
Author:Wayne L. Winston
Publisher:Brooks Cole
C++ Programming: From Problem Analysis to Program...
Computer Science
ISBN:9781337102087
Author:D. S. Malik
Publisher:Cengage Learning
Boolean Algebra - Digital Logic and Logic Families - Industrial Electronics; Author: Ekeeda;https://www.youtube.com/watch?v=u7XnJos-_Hs;License: Standard YouTube License, CC-BY
Boolean Algebra 1 – The Laws of Boolean Algebra; Author: Computer Science;https://www.youtube.com/watch?v=EPJf4owqwdA;License: Standard Youtube License