
Concept explainers
Astronauts on a distant planet toss a rock into the air. With the aid of a camera that takes pictures at a steady rate, they record the rock’s height as a function of time as given in the following table, (a) Find the rock’s average velocity in the time interval between each measurement and the next, (b) Using these average velocities to approximate instantaneous velocities at the midpoints of the lime intervals, make a graph of velocity as a function of time, (c) Does the rock move with constant acceleration? If so, plot a straight line of best fit on the graph and calculate its slope to find the acceleration.
(a)
The average velocity of rock in the time interval between each measurement and the next.
Answer to Problem 2.76AP
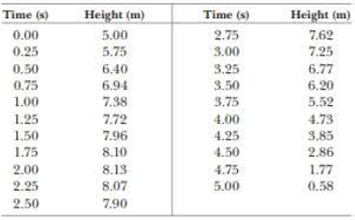
The rock’s height as a function of time is shown in below given table.
| Time (s) | Height (m) | Average velocity (
| Midpoint time (s) |
|
|
| ||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Table (1)
Explanation of Solution
Given info: The rock’s height as a function of time is shown in below given table.
| Time (s) | Height (m) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Table (2)
The formula to calculate the average velocity is,
Here,
The formula to calculate the midpoint time is,
Here,
Substitute the values given in table (1) and calculate the average velocity and midpoint time as mentioned in the table.
| Time (s) | Height (m) | Average velocity (
| Midpoint time (s) |
|
|
| ||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Table (3)
Conclusion:
Therefore, the rock’s height as a function of time is shown in below given table.
| Time (s) | Height (m) | Average velocity (
| Midpoint time (s) |
|
|
| ||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(b)
To draw: The velocity versus time graph.
Answer to Problem 2.76AP
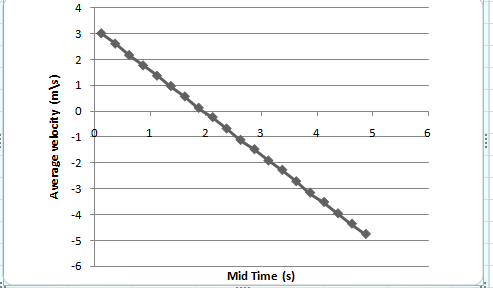
The average velocity versus mid time graph is,
Explanation of Solution
Introduction:
The velocity is defined as rate of change of position of the object. The Midpoint time is the mean of the time interval taken for which position of the object is defined. Plot the difference of the position with respect to midpoint time to obtain velocity time graph.
From part (a) make a graph using values of average velocity and mid time from table (1) as shown below.

Figure (1)
Conclusion:
Therefore, the average velocity versus mid time graph is,

(c)
Whether the rock moves with constant acceleration and determine the acceleration.
Answer to Problem 2.76AP
The rock moves with constant acceleration and the acceleration is
Explanation of Solution
The formula to calculate speed of rock from its graph in figure (1) is,
Substitute
Thus the slope of curve is
Hence, the acceleration of rock is
Conclusion:
Therefore, the rock moves with constant acceleration and the acceleration is
Want to see more full solutions like this?
Chapter 2 Solutions
EBK PHYSICS FOR SCIENTISTS AND ENGINEER
Additional Science Textbook Solutions
Campbell Essential Biology (7th Edition)
College Physics: A Strategic Approach (3rd Edition)
Fundamentals of Physics Extended
Chemistry: Structure and Properties (2nd Edition)
General, Organic, and Biological Chemistry - 4th edition
Cosmic Perspective Fundamentals
- Please help by: Use a free body diagram Show the equations State your assumptions Show your steps Box your final answer Thanks!arrow_forwardBy please don't use Chatgpt will upvote and give handwritten solutionarrow_forwardA collection of electric charges that share a common magnitude q (lower case) has been placed at the corners of a square, and an additional charge with magnitude Q (upper case) is located at the center of that square. The signs of the charges are indicated explicitly such that ∣∣+q∣∣∣∣+Q∣∣=∣∣−q∣∣==∣∣−Q∣∣=qQ Four unique setups of charges are displayed. By moving one of the direction drawings from near the bottom to the bucket beside each of the setups, indicate the direction of the net electric force on the charge with magnitude Q, located near the center, else indicate that the magnitude of the net electric force is zero, if appropriate.arrow_forward
- A number of electric charges has been placed at distinct points along a line with separations as indicated. Two charges share a common magnitude, q (lower case), and another charge has magnitude Q(upper case). The signs of the charges are indicated explicitly such that ∣∣+q∣∣∣∣+Q∣∣=∣∣−q∣∣==∣∣−Q∣∣=qQ Four different configurations of charges are shown. For each, express the net electric force on the charge with magnitude Q (upper case) as F⃗E=FE,xî where the positive x direction is towards the right. By repositioning the figures to the area on the right, rank the configurations from the most negative value to the most positive value of FE,x.arrow_forwardFor each part make sure to include sign to represent direction, with up being positive and down being negative. A ball is thrown vertically upward with a speed of 30.5 m/s. A) How high does it rise? y= B) How long does it take to reach its highest point? t= C) How long does it take the ball return to its starting point after it reaches its highest point? t= D) What is its velocity when it returns to the level from which it started? v=arrow_forwardFour point charges of equal magnitude Q = 55 nC are placed on the corners of a rectangle of sides D1 = 27 cm and D2 = 11cm. The charges on the left side of the rectangle are positive while the charges on the right side of the rectangle are negative. Use a coordinate system where the positive y-direction is up and the positive x-direction is to the right. A. Which of the following represents a free-body diagram for the charge on the lower left hand corner of the rectangle? B. Calculate the horizontal component of the net force, in newtons, on the charge which lies at the lower left corner of the rectangle.Numeric : A numeric value is expected and not an expression.Fx = __________________________________________NC. Calculate the vertical component of the net force, in newtons, on the charge which lies at the lower left corner of the rectangle.Numeric : A numeric value is expected and not an expression.Fy = __________________________________________ND. Calculate the magnitude of the…arrow_forward
- Point charges q1=50.0μC and q2=-35μC are placed d1=1.0m apart, as shown. A. A third charge, q3=25μC, is positioned somewhere along the line that passes through the first two charges, and the net force on q3 is zero. Which statement best describes the position of this third charge?1) Charge q3 is to the right of charge q2. 2) Charge q3 is between charges q1 and q2. 3) Charge q3 is to the left of charge q1. B. What is the distance, in meters, between charges q1 and q3? (Your response to the previous step may be used to simplify your solution.)Give numeric value.d2 = __________________________________________mC. Select option that correctly describes the change in the net force on charge q3 if the magnitude of its charge is increased.1) The magnitude of the net force on charge q3 would still be zero. 2) The effect depends upon the numeric value of charge q3. 3) The net force on charge q3 would be towards q2. 4) The net force on charge q3 would be towards q1. D. Select option that…arrow_forwardThe magnitude of the force between a pair of point charges is proportional to the product of the magnitudes of their charges and inversely proportional to the square of their separation distance. Four distinct charge-pair arrangements are presented. All charges are multiples of a common positive charge, q. All charge separations are multiples of a common length, L. Rank the four arrangements from smallest to greatest magnitude of the electric force.arrow_forwardA number of electric charges has been placed at distinct points along a line with separations as indicated. Two charges share a common magnitude, q (lower case), and another charge has magnitude Q (upper case). The signs of the charges are indicated explicitly such that ∣∣+q∣∣∣∣+Q∣∣=∣∣−q∣∣==∣∣−Q∣∣=qQ Four different configurations of charges are shown. For each, express the net electric force on the charge with magnitude Q (upper case) as F⃗E=FE,xî where the positive x direction is towards the right. By repositioning the figures to the area on the right, rank the configurations from the most negative value to the most positive value of FE,x.arrow_forward
 University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University
University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning An Introduction to Physical SciencePhysicsISBN:9781305079137Author:James Shipman, Jerry D. Wilson, Charles A. Higgins, Omar TorresPublisher:Cengage Learning
An Introduction to Physical SciencePhysicsISBN:9781305079137Author:James Shipman, Jerry D. Wilson, Charles A. Higgins, Omar TorresPublisher:Cengage Learning College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College
College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill
Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill





