FIRST COURSE IN PROBABILITY (LOOSELEAF)
10th Edition
ISBN: 9780134753751
Author: Ross
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 2, Problem 2.56P
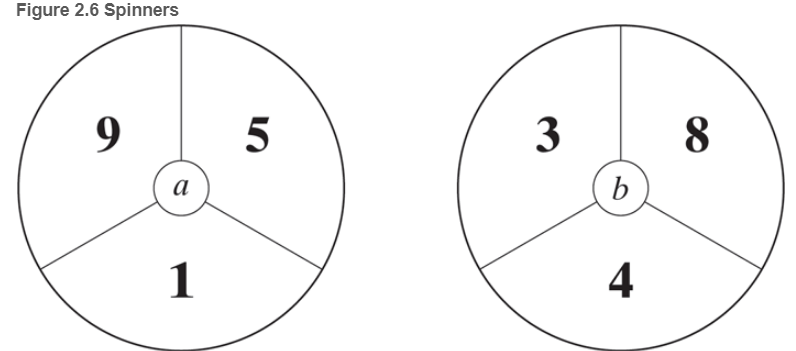
Two players play the following game: Player A chooses one of the three spinners pictured in Figure 2.6, and then player B chooses one of the remaining two spinners. Both players then spin their spinner, and the one that lands on the higher number is declared the winner. Assuming that each spinner is equally likely to land in any of its 3 regions, would you rather be player A or player B? Explain your answer!
Figure 2.6 Spinners
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
The same final exam of the astronomy course was given to two groups of students. The maximum number of points that a student can score is 100. The first group consisted of a random sample of 10 students who were taught by Professor A. Students from the first group obtained the following results:
87 88 91 88 86 92 81 93 73 99
The second group consisted of a random sample of 9 students who were taught by Professor B. Students from the second group obtained the following results:
74 74 79 97 67 88 86 83 78
Compute the mean squares of between-group variability, MSBET. Round your answer to two decimal places.
1. Consider the following preference ballots:
Number of voters
Rankings 6 5 4 2
1st choice A DCB
DC
2nd choice B B D
3rd choice DCBD
4th choice CA
AAA
For each of the four voting systems we have studied, determine who would win the election
in each case. (Remember: For plurality with runoff, all but the top two vote-getters are
simultaneously eliminated at the end of round 1.)
dangers of college kids carrying concealed handguns
Chapter 2 Solutions
FIRST COURSE IN PROBABILITY (LOOSELEAF)
Ch. 2 - A box contains 3 marbles: 1 red, 1 green, and 1...Ch. 2 - In an experiment, die is rolled continually until...Ch. 2 - Two dice are thrown. Let E be the event that the...Ch. 2 - A, B, and C take turns flipping a coin. The first...Ch. 2 - A system is composed of 5 components, each of...Ch. 2 - A hospital administrator codes incoming patients...Ch. 2 - Consider an experiment that consists of...Ch. 2 - Suppose that A and B are mutually exclusive events...Ch. 2 - A retail establishment accepts either the American...Ch. 2 - Sixty percent of the students at a certain school...
Ch. 2 - A total of 28 percent of American males smoke...Ch. 2 - An elementary school is offering 3 language...Ch. 2 - A certain town with a population of 100.000 has 3...Ch. 2 - The following data were given in a study of a...Ch. 2 - If it is assumed that all (525) poker hands are...Ch. 2 - Poker dice is played by simultaneously rolling 5...Ch. 2 - Twenty five people, consisting of 15 women and 10...Ch. 2 - Two cards are randomly selected from an ordinary...Ch. 2 - Two symmetric dice have had two of their sides...Ch. 2 - Suppose that you are playing blackjack against a...Ch. 2 - A small community organization consists of 20...Ch. 2 - Consider the following technique for shuffling a...Ch. 2 - A pair of fair dice is rolled. What is the...Ch. 2 - It two dice are rolled, what is the probability...Ch. 2 - A pair of dice is rolled until a sum of either 5...Ch. 2 - The game of craps is played as follows: A player...Ch. 2 - An urn contains 3 red and 7 black balls. Players A...Ch. 2 - An urn contains 5 red, 6 blue, and 8 green balls....Ch. 2 - An urn contains n white and m black balls, where n...Ch. 2 - The chess clubs of two schools consist of,...Ch. 2 - A 3-person basketball team consists of a guard, a...Ch. 2 - A group of individuals containing b boys and g...Ch. 2 - A forest contains 20 elk, of which 5 are captured,...Ch. 2 - The second Earl of Yarborough is reported to have...Ch. 2 - Seven balls are randomly withdrawn from an urn...Ch. 2 - Two cards are chosen at random from a deck of 52...Ch. 2 - An instructor gives her class a set of 10 problems...Ch. 2 - There are n socks. 3 of which are red, in a...Ch. 2 - There are 5 hotels in a certain town. If 3 people...Ch. 2 - If 4 balls are randomly chosen from an urn...Ch. 2 - If a die is rolled 4 times, what is the...Ch. 2 - Two dice are thrown n times in succession. Compute...Ch. 2 - a. If N people, including A and B, are randomly...Ch. 2 - Five people, designated as A, B, C, D, E, are...Ch. 2 - A woman has n keys, of which one will open her...Ch. 2 - How many people have to be in a room in order that...Ch. 2 - Suppose that 5 of the numbers 1, 2,..., 14 are...Ch. 2 - Given 20 people, what is the probability that...Ch. 2 - A group of 6 men and 6 women is randomly divided...Ch. 2 - In a hand of bridge, find the probability that you...Ch. 2 - Suppose that n balls are randomly distributed into...Ch. 2 - A closet contains 10 pairs of shoes. If 8 shoes...Ch. 2 - If 8 people, consisting of 4 couples, are randomly...Ch. 2 - Compute the probability that a bridge hand is void...Ch. 2 - Compute the probability that a hand of 13 cards...Ch. 2 - Two players play the following game: Player A...Ch. 2 - Prove the following relations: EFEEFCh. 2 - Prove the following relations: If EF, then FCEC.Ch. 2 - Prove the following relations: 3. F=FEFEC and...Ch. 2 - Prove the following relations: (1Ei)F=1EiF and...Ch. 2 - For any sequence of events E1,E2,..., define a new...Ch. 2 - Let E, F, and C be three events. Find expressions...Ch. 2 - Use Venn diagrams a. to simplify the expression...Ch. 2 - Prob. 2.8TECh. 2 - Suppose that an experiment is performed n times...Ch. 2 - Prove...Ch. 2 - If P(E)=.9 and P(F)=.8, show that P(EF).7. In...Ch. 2 - Show that the probability that exactly one of the...Ch. 2 - Prove that P(EF)=P(E)P(EF).Ch. 2 - Prove Proposition 4.4 by mathematical induction.Ch. 2 - An urn contains M white and N black balls. If a...Ch. 2 - Use induction to generalize Bonferronis inequality...Ch. 2 - Consider the matching problem. Example 5m, and...Ch. 2 - Let fn, denote the number of ways of tossing a...Ch. 2 - An urn contains n red and m blue balls. They are...Ch. 2 - Consider an experiment whose sample space consists...Ch. 2 - Consider Example 50, which is concerned with the...Ch. 2 - A cafeteria offers a three-course meal consisting...Ch. 2 - A customer visiting the suit department of a...Ch. 2 - A deck of cards is dealt out. What is the...Ch. 2 - Let A denote the event that the midtown...Ch. 2 - An ordinary deck of 52 cards is shuffled. What is...Ch. 2 - Urn A contains 3 red and 3 black balls, whereas...Ch. 2 - In a state lottery, a player must choose 8 of the...Ch. 2 - From a group of 3 first-year students, 4...Ch. 2 - For a finite set A, let N(A) denote the number of...Ch. 2 - Consider an experiment that consists of 6 horses,...Ch. 2 - A 5-card hand is dealt from a well-shuffled deck...Ch. 2 - A basketball team consists of 6 frontcourt and 4...Ch. 2 - Suppose that a person chooses a letter at random...Ch. 2 - Prove Booles inequality P(i=1Ai)i=1P(Ai)Ch. 2 - Show that if P(Ai)=1 for all i1, then P(i=1Ai)=1.Ch. 2 - Let Tk(n) denote the number of partitions of the...Ch. 2 - Five balls are randomly chosen, without...Ch. 2 - Four red, 8 blue, and 5 green balls are randomly...Ch. 2 - Ten cards are randomly chosen from a deck of 52...Ch. 2 - Balls are randomly removed from an urn initially...
Additional Math Textbook Solutions
Find more solutions based on key concepts
Use the ideas in drawings a and b to find the solution to Gausss Problem for the sum 1+2+3+...+n. Explain your ...
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
The largest polynomial that divides evenly into a list of polynomials is called the _______.
Elementary & Intermediate Algebra
Length of a Guy Wire A communications tower is located at the top of a steep hill, as shown. The angle of incli...
Precalculus: Mathematics for Calculus (Standalone Book)
For Exercises 13–18, write the negation of the statement.
13. The cell phone is out of juice.
Math in Our World
In Exercises 9-20, use the data in the following table, which lists drive-thru order accuracy at popular fast f...
Elementary Statistics (13th Edition)
Teacher Salaries
The following data from several years ago represent salaries (in dollars) from a school distri...
Elementary Statistics: A Step By Step Approach
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, probability and related others by exploring similar questions and additional content below.Similar questions
- iid B1 Suppose X1, ..., Xn fx(x), where 2 fx(x) = x exp(−x²/0), 0<< (0 otherwise). (a) Find the maximum likelihood estimator of 0. (b) Show that the MLE is an unbiased estimator of 0. (c) Find the MSE of the MLE. Hint: For parts (b) and (c), you may use integration by parts.arrow_forwardiid B1 Suppose X1, ..., Xn fx(x), where 2 fx(x) = x exp(−x²/0), 0<< (0 otherwise). (a) Find the maximum likelihood estimator of 0. (b) Show that the MLE is an unbiased estimator of 0. (c) Find the MSE of the MLE. Hint: For parts (b) and (c), you may use integration by parts.arrow_forward2) Suppose we select two values x and y independently from the uniform distribution on [0,1]. What is the probability that xyarrow_forward100 identical balls are rolling along a straight line. They all have speed equal to v, but some of them might move in opposite directions. When two of them collide they immediately switch their direction and keep the speed v. What is the maximum number of collisions that can happen? Let f(w) be a function of vector w Є RN, i.e. f(w) = 1+e Determine the first derivative and matrix of second derivatives off with respect to w. Let A Є RN*N be a symmetric, positive definite matrix and bЄ RN a vector. If x ER, evaluate the integral Z(A,b) = e¯xAx+bx dx as a function of A and b. John throws a fair die with faces labelled 1 to 6. ⚫ He gains 10 points if the die shows 1. ⚫ He gains 1 point if the die shows 2 or 4. • No points are allocated otherwise. Let X be the random variable describing John's gain at each throw. Determine the variance of X.arrow_forwardFemale Male Totals Less than High School Diploma 0.077 0.110 0.187 High School Diploma 0.154 0.201 0.355 Some College/University 0.141 0.129 0.270 College/University Graduate 0.092 0.096 0.188 Totals 0.464 0.536 1.000arrow_forwardFemale Male Totals Less than High School Diploma 0.077 0.110 0.187 High School Diploma 0.154 0.201 0.355 Some College/University 0.141 0.129 0.270 College/University Graduate 0.092 0.096 0.188 Totals 0.464 0.536 1.000arrow_forwardFemale Male Totals Less than High School Diploma 0.077 0.110 0.187 High School Diploma 0.154 0.201 0.355 Some College/University 0.141 0.129 0.270 College/University Graduate 0.092 0.096 0.188 Totals 0.464 0.536 1.000arrow_forwardFemale Male Totals Less than High School Diploma 0.077 0.110 0.187 High School Diploma 0.154 0.201 0.355 Some College/University 0.141 0.129 0.270 College/University Graduate 0.092 0.096 0.188 Totals 0.464 0.536 1.000arrow_forward6.54 Let Y₁, Y2,..., Y, be independent Poisson random variables with means 1, 2,..., An respectively. Find the a probability function of Y. b conditional probability function of Y₁, given that Y = m. Y₁ = m. c conditional probability function of Y₁+Y2, given that 6.55 Customers arrive at a department store checkout counter according to a Poisson distribution with a mean of 7 per hour. In a given two-hour period, what is the probability that 20 or more customers will arrive at the counter? 6.56 The length of time necessary to tune up a car is exponentially distributed with a mean of .5 hour. If two cars are waiting for a tune-up and the service times are independent, what is the probability that the total time for the two tune-ups will exceed 1.5 hours? [Hint: Recall the result of Example 6.12.] 6.57 Let Y, Y2,..., Y,, be independent random variables such that each Y, has a gamma distribution with parameters a, and B. That is, the distributions of the Y's might have different a's, but…arrow_forward6.82 6.83 6.84 6.85 *6.86 6.87 If Y is a continuous random variable and m is the median of the distribution, then m is such that P(Ym) = P(Y ≥ m) = 1/2. If Y₁, Y2,..., Y, are independent, exponentially dis- tributed random variables with mean ẞ and median m, Example 6.17 implies that Y(n) = max(Y₁, Y., Y) does not have an exponential distribution. Use the general form of FY() (y) to show that P(Y(n) > m) = 1 - (.5)". Refer to Exercise 6.82. If Y₁, Y2,..., Y,, is a random sample from any continuous distribution with mean m, what is P(Y(n) > m)? Refer to Exercise 6.26. The Weibull density function is given by -my" m-le-y/a f(y)= α 0. y > 0, elsewhere, where a and m are positive constants. If a random sample of size n is taken from a Weibull distributed population, find the distribution function and density function for Y(1) = min(Y1, Y2,Y). Does Y(1) = have a Weibull distribution? Let Y₁ and Y2 be independent and uniformly distributed over the interval (0, 1). Find P(2Y(1) 0, elsewhere,…arrow_forward6.26 The Weibull density function is given by e-y/a f(y) = α 0. y > 0, elsewhere, where a and m are positive constants. This density function is often used as a model for the lengths of life of physical systems. Suppose Y has the Weibull density just given. Find a the density function of UY". b E(Y) for any positive integer k. 6.27 Let Y have an exponential distribution with mean ẞ. 6.28 6.29 a Prove that W = √Y has a Weibull density with α = ẞ and m = 2. b Use the result in Exercise 6.26(b) to give E(Yk/2) for any positive integer k. Let Y have a uniform (0, 1) distribution. Show that U = -2ln(Y) has an exponential distri- bution with mean 2. The speed of a molecule in a uniform gas at equilibrium is a random variable V whose density function is given by 6.30 6.31 6.32 f(v) = av²e-by², v > 0, where b = m/2kT and k, T, and m denote Boltzmann's constant, the absolute temperature, and the mass of the molecule, respectively. a Derive the distribution of W = mV2/2, the kinetic energy of…arrow_forwardQIA Let F-4c24, countible or, A, countible), show that is o-algebra. B Let (Fne N) is family of a-algebra on 2, prove that F. o-algebra Q2: Prove that: 1. X, is martingale -esin 2. M, -e sin B,, is martingale by using Ito formula Q3: A Let X, has stochastic differential with drift p(x)=-bx + c, and diffusion o²(x)=4x, let Y√X,, where X, ≥0, find dr B: Let X, -(-s), Ito integral process, find dx, and [x.xko). Q4: Let Y, =[x,dB, is Ito integral, such that X, is nonrandom process, find: التوزيع 1. The distribution of Y 2. The moment generating function of Y,.arrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
Recommended textbooks for you
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill
Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL
Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning
Solve ANY Optimization Problem in 5 Steps w/ Examples. What are they and How do you solve them?; Author: Ace Tutors;https://www.youtube.com/watch?v=BfOSKc_sncg;License: Standard YouTube License, CC-BY
Types of solution in LPP|Basic|Multiple solution|Unbounded|Infeasible|GTU|Special case of LP problem; Author: Mechanical Engineering Management;https://www.youtube.com/watch?v=F-D2WICq8Sk;License: Standard YouTube License, CC-BY
Optimization Problems in Calculus; Author: Professor Dave Explains;https://www.youtube.com/watch?v=q1U6AmIa_uQ;License: Standard YouTube License, CC-BY
Introduction to Optimization; Author: Math with Dr. Claire;https://www.youtube.com/watch?v=YLzgYm2tN8E;License: Standard YouTube License, CC-BY