EBK ALGEBRA 2
11th Edition
ISBN: 9780544714304
Author: Larson
Publisher: HMH PUB
expand_more
expand_more
format_list_bulleted
Videos
Expert Solution & Answer
Chapter 2, Problem 20TP
Solution
a.
To find: How long you should make the cuts?
The cuts should be
Given information:
You are making an open box to hold paper clips out of a piece of cardboard that is 5 inches by 8 inches. The box will be formed by making the cuts as shown in the diagram and folding up the sides. You want the box to have the greatest volume possible.
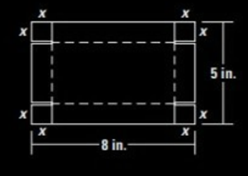
Formula used:
Volume of rectangular box is length times width times the height of the box.
Calculation:
The box will be formed by making the cuts of
The length of the box would be
To find the maximum volume, graph the volume function on a graphing calculator. Consider only the interval
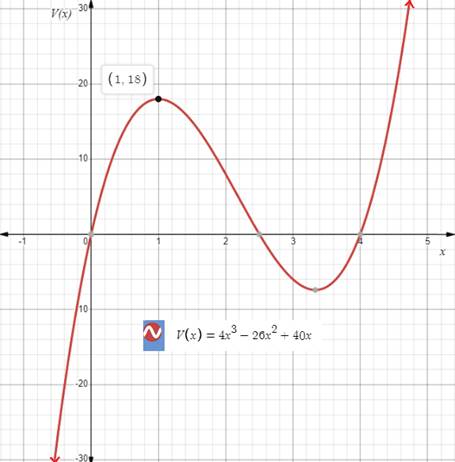
It is visible that the maximum volume occurs when
b.
To find: What is the maximum volume of the box?
The maximum volume of the box would be
Given information:
You are making an open box to hold paper clips out of a piece of cardboard that is 5 inches by 8 inches. The box will be formed by making the cuts as shown in the diagram and folding up the sides. You want the box to have the greatest volume possible.
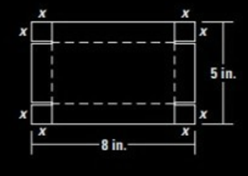
Formula used:
Volume of rectangular box is length times width times the height of the box.
Calculation:
From the graph in part (a), it is visible that the maximum volume is about
c.
To find: What will the dimensions of the finished box be?
The dimensions of the box will be
Given information:
You are making an open box to hold paper clips out of a piece of cardboard that is 5 inches by 8 inches. The box will be formed by making the cuts as shown in the diagram and folding up the sides. You want the box to have the greatest volume possible.
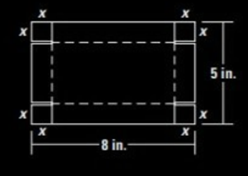
Formula used:
Volume of rectangular box is length times width times the height of the box.
Calculation:
To find the dimensions of box, use
Length of the box would be:
Width of the box would be:
Therefore, the dimensions of the box will be
Chapter 2 Solutions
EBK ALGEBRA 2
Ch. 2.1 - Prob. 1GPCh. 2.1 - Prob. 2GPCh. 2.1 - Prob. 3GPCh. 2.1 - Prob. 4GPCh. 2.1 - Prob. 5GPCh. 2.1 - Prob. 6GPCh. 2.1 - Prob. 7GPCh. 2.1 - Prob. 8GPCh. 2.1 - Prob. 1ECh. 2.1 - Prob. 2E
Ch. 2.1 - Prob. 3ECh. 2.1 - Prob. 4ECh. 2.1 - Prob. 5ECh. 2.1 - Prob. 6ECh. 2.1 - Prob. 7ECh. 2.1 - Prob. 8ECh. 2.1 - Prob. 9ECh. 2.1 - Prob. 10ECh. 2.1 - Prob. 11ECh. 2.1 - Prob. 12ECh. 2.1 - Prob. 13ECh. 2.1 - Prob. 14ECh. 2.1 - Prob. 15ECh. 2.1 - Prob. 16ECh. 2.1 - Prob. 17ECh. 2.1 - Prob. 18ECh. 2.1 - Prob. 19ECh. 2.1 - Prob. 20ECh. 2.1 - Prob. 21ECh. 2.1 - Prob. 22ECh. 2.1 - Prob. 23ECh. 2.1 - Prob. 24ECh. 2.1 - Prob. 25ECh. 2.1 - Prob. 26ECh. 2.1 - Prob. 27ECh. 2.1 - Prob. 28ECh. 2.1 - Prob. 29ECh. 2.1 - Prob. 30ECh. 2.1 - Prob. 31ECh. 2.1 - Prob. 32ECh. 2.1 - Prob. 33ECh. 2.1 - Prob. 34ECh. 2.1 - Prob. 35ECh. 2.1 - Prob. 36ECh. 2.1 - Prob. 37ECh. 2.1 - Prob. 38ECh. 2.1 - Prob. 39ECh. 2.1 - Prob. 40ECh. 2.1 - Prob. 41ECh. 2.1 - Prob. 42ECh. 2.1 - Prob. 43ECh. 2.1 - Prob. 44ECh. 2.1 - Prob. 45ECh. 2.1 - Prob. 46ECh. 2.1 - Prob. 47ECh. 2.1 - Prob. 48ECh. 2.1 - Prob. 49PSCh. 2.1 - Prob. 50PSCh. 2.1 - Prob. 51PSCh. 2.1 - Prob. 52PSCh. 2.1 - Prob. 53PSCh. 2.1 - Prob. 54PSCh. 2.1 - Prob. 1DCCh. 2.1 - Prob. 2DCCh. 2.1 - Prob. 3DCCh. 2.1 - Prob. 4DCCh. 2.1 - Prob. 5DCCh. 2.1 - Prob. 6DCCh. 2.2 - Prob. 1GPCh. 2.2 - Prob. 2GPCh. 2.2 - Prob. 3GPCh. 2.2 - Prob. 4GPCh. 2.2 - Prob. 5GPCh. 2.2 - Prob. 6GPCh. 2.2 - Prob. 7GPCh. 2.2 - Prob. 8GPCh. 2.2 - Prob. 9GPCh. 2.2 - Prob. 10GPCh. 2.2 - Prob. 11GPCh. 2.2 - Prob. 12GPCh. 2.2 - Prob. 1ECh. 2.2 - Prob. 2ECh. 2.2 - Prob. 3ECh. 2.2 - Prob. 4ECh. 2.2 - Prob. 5ECh. 2.2 - Prob. 6ECh. 2.2 - Prob. 7ECh. 2.2 - Prob. 8ECh. 2.2 - Prob. 9ECh. 2.2 - Prob. 10ECh. 2.2 - Prob. 11ECh. 2.2 - Prob. 12ECh. 2.2 - Prob. 13ECh. 2.2 - Prob. 14ECh. 2.2 - Prob. 15ECh. 2.2 - Prob. 16ECh. 2.2 - Prob. 17ECh. 2.2 - Prob. 18ECh. 2.2 - Prob. 19ECh. 2.2 - Prob. 20ECh. 2.2 - Prob. 21ECh. 2.2 - Prob. 22ECh. 2.2 - Prob. 23ECh. 2.2 - Prob. 24ECh. 2.2 - Prob. 25ECh. 2.2 - Prob. 26ECh. 2.2 - Prob. 27ECh. 2.2 - Prob. 28ECh. 2.2 - Prob. 29ECh. 2.2 - Prob. 30ECh. 2.2 - Prob. 31ECh. 2.2 - Prob. 32ECh. 2.2 - Prob. 33ECh. 2.2 - Prob. 34ECh. 2.2 - Prob. 35ECh. 2.2 - Prob. 36ECh. 2.2 - Prob. 37ECh. 2.2 - Prob. 38ECh. 2.2 - Prob. 39ECh. 2.2 - Prob. 40ECh. 2.2 - Prob. 41ECh. 2.2 - Prob. 42ECh. 2.2 - Prob. 43ECh. 2.2 - Prob. 44ECh. 2.2 - Prob. 45ECh. 2.2 - Prob. 46ECh. 2.2 - Prob. 47ECh. 2.2 - Prob. 48ECh. 2.2 - Prob. 49ECh. 2.2 - Prob. 50ECh. 2.2 - Prob. 51ECh. 2.2 - Prob. 52ECh. 2.2 - Prob. 53ECh. 2.2 - Prob. 54PSCh. 2.2 - Prob. 55PSCh. 2.2 - Prob. 56PSCh. 2.2 - Prob. 57PSCh. 2.2 - Prob. 58PSCh. 2.2 - Prob. 59PSCh. 2.2 - Prob. 60PSCh. 2.2 - Prob. 1PCh. 2.2 - Prob. 2PCh. 2.2 - Prob. 3PCh. 2.2 - Prob. 4PCh. 2.2 - Prob. 5PCh. 2.2 - Prob. 6PCh. 2.2 - Prob. 7PCh. 2.2 - Prob. 8PCh. 2.2 - Prob. 9PCh. 2.2 - Prob. 10PCh. 2.3 - Prob. 1GPCh. 2.3 - Prob. 2GPCh. 2.3 - Prob. 3GPCh. 2.3 - Prob. 4GPCh. 2.3 - Prob. 5GPCh. 2.3 - Prob. 6GPCh. 2.3 - Prob. 1ECh. 2.3 - Prob. 2ECh. 2.3 - Prob. 3ECh. 2.3 - Prob. 4ECh. 2.3 - Prob. 5ECh. 2.3 - Prob. 6ECh. 2.3 - Prob. 7ECh. 2.3 - Prob. 8ECh. 2.3 - Prob. 9ECh. 2.3 - Prob. 10ECh. 2.3 - Prob. 11ECh. 2.3 - Prob. 12ECh. 2.3 - Prob. 13ECh. 2.3 - Prob. 14ECh. 2.3 - Prob. 15ECh. 2.3 - Prob. 16ECh. 2.3 - Prob. 17ECh. 2.3 - Prob. 18ECh. 2.3 - Prob. 19ECh. 2.3 - Prob. 20ECh. 2.3 - Prob. 21ECh. 2.3 - Prob. 22ECh. 2.3 - Prob. 23ECh. 2.3 - Prob. 24ECh. 2.3 - Prob. 25ECh. 2.3 - Prob. 26ECh. 2.3 - Prob. 27ECh. 2.3 - Prob. 28ECh. 2.3 - Prob. 29ECh. 2.3 - Prob. 30ECh. 2.3 - Prob. 31ECh. 2.3 - Prob. 32ECh. 2.3 - Prob. 33ECh. 2.3 - Prob. 34ECh. 2.3 - Prob. 35ECh. 2.3 - Prob. 36ECh. 2.3 - Prob. 37ECh. 2.3 - Prob. 38ECh. 2.3 - Prob. 39ECh. 2.3 - Prob. 40ECh. 2.3 - Prob. 41ECh. 2.3 - Prob. 42ECh. 2.3 - Prob. 43ECh. 2.3 - Prob. 44ECh. 2.3 - Prob. 45ECh. 2.3 - Prob. 46ECh. 2.3 - Prob. 47ECh. 2.3 - Prob. 48ECh. 2.3 - Prob. 49ECh. 2.3 - Prob. 50ECh. 2.3 - Prob. 51ECh. 2.3 - Prob. 52ECh. 2.3 - Prob. 53ECh. 2.3 - Prob. 54ECh. 2.3 - Prob. 55ECh. 2.3 - Prob. 56ECh. 2.3 - Prob. 57ECh. 2.3 - Prob. 58ECh. 2.3 - Prob. 59PSCh. 2.3 - Prob. 60PSCh. 2.3 - Prob. 61PSCh. 2.3 - Prob. 62PSCh. 2.3 - Prob. 63PSCh. 2.3 - Prob. 64PSCh. 2.3 - Prob. 1QCh. 2.3 - Prob. 2QCh. 2.3 - Prob. 3QCh. 2.3 - Prob. 4QCh. 2.3 - Prob. 5QCh. 2.3 - Prob. 6QCh. 2.3 - Prob. 7QCh. 2.3 - Prob. 8QCh. 2.3 - Prob. 9QCh. 2.3 - Prob. 10QCh. 2.3 - Prob. 11QCh. 2.3 - Prob. 12QCh. 2.3 - Prob. 13QCh. 2.3 - Prob. 14QCh. 2.3 - Prob. 15QCh. 2.3 - Prob. 16QCh. 2.4 - Prob. 1GPCh. 2.4 - Prob. 2GPCh. 2.4 - Prob. 3GPCh. 2.4 - Prob. 4GPCh. 2.4 - Prob. 5GPCh. 2.4 - Prob. 6GPCh. 2.4 - Prob. 7GPCh. 2.4 - Prob. 8GPCh. 2.4 - Prob. 9GPCh. 2.4 - Prob. 10GPCh. 2.4 - Prob. 11GPCh. 2.4 - Prob. 1ECh. 2.4 - Prob. 2ECh. 2.4 - Prob. 3ECh. 2.4 - Prob. 4ECh. 2.4 - Prob. 5ECh. 2.4 - Prob. 6ECh. 2.4 - Prob. 7ECh. 2.4 - Prob. 8ECh. 2.4 - Prob. 9ECh. 2.4 - Prob. 10ECh. 2.4 - Prob. 11ECh. 2.4 - Prob. 12ECh. 2.4 - Prob. 13ECh. 2.4 - Prob. 14ECh. 2.4 - Prob. 15ECh. 2.4 - Prob. 16ECh. 2.4 - Prob. 17ECh. 2.4 - Prob. 18ECh. 2.4 - Prob. 19ECh. 2.4 - Prob. 20ECh. 2.4 - Prob. 21ECh. 2.4 - Prob. 22ECh. 2.4 - Prob. 23ECh. 2.4 - Prob. 24ECh. 2.4 - Prob. 25ECh. 2.4 - Prob. 26ECh. 2.4 - Prob. 27ECh. 2.4 - Prob. 28ECh. 2.4 - Prob. 29ECh. 2.4 - Prob. 30ECh. 2.4 - Prob. 31ECh. 2.4 - Prob. 32ECh. 2.4 - Prob. 33ECh. 2.4 - Prob. 34ECh. 2.4 - Prob. 35ECh. 2.4 - Prob. 36ECh. 2.4 - Prob. 37ECh. 2.4 - Prob. 38ECh. 2.4 - Prob. 39ECh. 2.4 - Prob. 40ECh. 2.4 - Prob. 41ECh. 2.4 - Prob. 42ECh. 2.4 - Prob. 43ECh. 2.4 - Prob. 44ECh. 2.4 - Prob. 45ECh. 2.4 - Prob. 46ECh. 2.4 - Prob. 47ECh. 2.4 - Prob. 48ECh. 2.4 - Prob. 49ECh. 2.4 - Prob. 50ECh. 2.4 - Prob. 51ECh. 2.4 - Prob. 52ECh. 2.4 - Prob. 53ECh. 2.4 - Prob. 54ECh. 2.4 - Prob. 55ECh. 2.4 - Prob. 56ECh. 2.4 - Prob. 57ECh. 2.4 - Prob. 58PSCh. 2.4 - Prob. 59PSCh. 2.4 - Prob. 60PSCh. 2.4 - Prob. 61PSCh. 2.4 - Prob. 62PSCh. 2.4 - Prob. 63PSCh. 2.4 - Prob. 64PSCh. 2.4 - Prob. 65PSCh. 2.4 - Prob. 1PCh. 2.4 - Prob. 2PCh. 2.4 - Prob. 3PCh. 2.4 - Prob. 4PCh. 2.4 - Prob. 5PCh. 2.4 - Prob. 6PCh. 2.4 - Prob. 7PCh. 2.4 - Prob. 8PCh. 2.4 - Prob. 9PCh. 2.4 - Prob. 10PCh. 2.5 - Prob. 1GPCh. 2.5 - Prob. 2GPCh. 2.5 - Prob. 3GPCh. 2.5 - Prob. 4GPCh. 2.5 - Prob. 5GPCh. 2.5 - Prob. 6GPCh. 2.5 - Prob. 7GPCh. 2.5 - Prob. 8GPCh. 2.5 - Prob. 9GPCh. 2.5 - Prob. 1ECh. 2.5 - Prob. 2ECh. 2.5 - Prob. 3ECh. 2.5 - Prob. 4ECh. 2.5 - Prob. 5ECh. 2.5 - Prob. 6ECh. 2.5 - Prob. 7ECh. 2.5 - Prob. 8ECh. 2.5 - Prob. 9ECh. 2.5 - Prob. 10ECh. 2.5 - Prob. 11ECh. 2.5 - Prob. 12ECh. 2.5 - Prob. 13ECh. 2.5 - Prob. 14ECh. 2.5 - Prob. 15ECh. 2.5 - Prob. 16ECh. 2.5 - Prob. 17ECh. 2.5 - Prob. 18ECh. 2.5 - Prob. 19ECh. 2.5 - Prob. 20ECh. 2.5 - Prob. 21ECh. 2.5 - Prob. 22ECh. 2.5 - Prob. 23ECh. 2.5 - Prob. 24ECh. 2.5 - Prob. 25ECh. 2.5 - Prob. 26ECh. 2.5 - Prob. 27ECh. 2.5 - Prob. 28ECh. 2.5 - Prob. 29ECh. 2.5 - Prob. 30ECh. 2.5 - Prob. 31ECh. 2.5 - Prob. 32ECh. 2.5 - Prob. 33ECh. 2.5 - Prob. 34ECh. 2.5 - Prob. 35ECh. 2.5 - Prob. 36ECh. 2.5 - Prob. 37ECh. 2.5 - Prob. 38ECh. 2.5 - Prob. 39ECh. 2.5 - Prob. 40ECh. 2.5 - Prob. 41PSCh. 2.5 - Prob. 42PSCh. 2.5 - Prob. 43PSCh. 2.5 - Prob. 44PSCh. 2.5 - Prob. 45PSCh. 2.5 - Prob. 46PSCh. 2.5 - Prob. 1MRPSCh. 2.5 - Prob. 2MRPSCh. 2.5 - Prob. 3MRPSCh. 2.5 - Prob. 4MRPSCh. 2.5 - Prob. 5MRPSCh. 2.5 - Prob. 6MRPSCh. 2.5 - Prob. 7MRPSCh. 2.6 - Prob. 1GPCh. 2.6 - Prob. 2GPCh. 2.6 - Prob. 3GPCh. 2.6 - Prob. 4GPCh. 2.6 - Prob. 5GPCh. 2.6 - Prob. 6GPCh. 2.6 - Prob. 7GPCh. 2.6 - Prob. 1ECh. 2.6 - Prob. 2ECh. 2.6 - Prob. 3ECh. 2.6 - Prob. 4ECh. 2.6 - Prob. 5ECh. 2.6 - Prob. 6ECh. 2.6 - Prob. 7ECh. 2.6 - Prob. 8ECh. 2.6 - Prob. 9ECh. 2.6 - Prob. 10ECh. 2.6 - Prob. 11ECh. 2.6 - Prob. 12ECh. 2.6 - Prob. 13ECh. 2.6 - Prob. 14ECh. 2.6 - Prob. 15ECh. 2.6 - Prob. 16ECh. 2.6 - Prob. 17ECh. 2.6 - Prob. 18ECh. 2.6 - Prob. 19ECh. 2.6 - Prob. 20ECh. 2.6 - Prob. 21ECh. 2.6 - Prob. 22ECh. 2.6 - Prob. 23ECh. 2.6 - Prob. 24ECh. 2.6 - Prob. 25ECh. 2.6 - Prob. 26ECh. 2.6 - Prob. 27ECh. 2.6 - Prob. 28ECh. 2.6 - Prob. 29ECh. 2.6 - Prob. 30ECh. 2.6 - Prob. 31ECh. 2.6 - Prob. 32ECh. 2.6 - Prob. 33ECh. 2.6 - Prob. 34ECh. 2.6 - Prob. 35ECh. 2.6 - Prob. 36ECh. 2.6 - Prob. 37ECh. 2.6 - Prob. 38ECh. 2.6 - Prob. 39ECh. 2.6 - Prob. 40ECh. 2.6 - Prob. 41ECh. 2.6 - Prob. 42ECh. 2.6 - Prob. 43ECh. 2.6 - Prob. 44ECh. 2.6 - Prob. 45PSCh. 2.6 - Prob. 46PSCh. 2.6 - Prob. 47PSCh. 2.6 - Prob. 48PSCh. 2.6 - Prob. 49PSCh. 2.6 - Prob. 50PSCh. 2.6 - Prob. 51PSCh. 2.6 - Prob. 1QCh. 2.6 - Prob. 2QCh. 2.6 - Prob. 3QCh. 2.6 - Prob. 4QCh. 2.6 - Prob. 5QCh. 2.6 - Prob. 6QCh. 2.6 - Prob. 7QCh. 2.6 - Prob. 8QCh. 2.6 - Prob. 9QCh. 2.6 - Prob. 10QCh. 2.6 - Prob. 11QCh. 2.6 - Prob. 12QCh. 2.6 - Prob. 13QCh. 2.6 - Prob. 1PCh. 2.6 - Prob. 2PCh. 2.6 - Prob. 3PCh. 2.6 - Prob. 4PCh. 2.7 - Prob. 1GPCh. 2.7 - Prob. 2GPCh. 2.7 - Prob. 3GPCh. 2.7 - Prob. 4GPCh. 2.7 - Prob. 5GPCh. 2.7 - Prob. 6GPCh. 2.7 - Prob. 7GPCh. 2.7 - Prob. 8GPCh. 2.7 - Prob. 9GPCh. 2.7 - Prob. 10GPCh. 2.7 - Prob. 11GPCh. 2.7 - Prob. 12GPCh. 2.7 - Prob. 1ECh. 2.7 - Prob. 2ECh. 2.7 - Prob. 3ECh. 2.7 - Prob. 4ECh. 2.7 - Prob. 5ECh. 2.7 - Prob. 6ECh. 2.7 - Prob. 7ECh. 2.7 - Prob. 8ECh. 2.7 - Prob. 9ECh. 2.7 - Prob. 10ECh. 2.7 - Prob. 11ECh. 2.7 - Prob. 12ECh. 2.7 - Prob. 13ECh. 2.7 - Prob. 14ECh. 2.7 - Prob. 15ECh. 2.7 - Prob. 16ECh. 2.7 - Prob. 17ECh. 2.7 - Prob. 18ECh. 2.7 - Prob. 19ECh. 2.7 - Prob. 20ECh. 2.7 - Prob. 21ECh. 2.7 - Prob. 22ECh. 2.7 - Prob. 23ECh. 2.7 - Prob. 24ECh. 2.7 - Prob. 25ECh. 2.7 - Prob. 26ECh. 2.7 - Prob. 27ECh. 2.7 - Prob. 28ECh. 2.7 - Prob. 29ECh. 2.7 - Prob. 30ECh. 2.7 - Prob. 31ECh. 2.7 - Prob. 32ECh. 2.7 - Prob. 33ECh. 2.7 - Prob. 34ECh. 2.7 - Prob. 35ECh. 2.7 - Prob. 36ECh. 2.7 - Prob. 37ECh. 2.7 - Prob. 38ECh. 2.7 - Prob. 39ECh. 2.7 - Prob. 40ECh. 2.7 - Prob. 41ECh. 2.7 - Prob. 42ECh. 2.7 - Prob. 43ECh. 2.7 - Prob. 44ECh. 2.7 - Prob. 45ECh. 2.7 - Prob. 46ECh. 2.7 - Prob. 47ECh. 2.7 - Prob. 48ECh. 2.7 - Prob. 49ECh. 2.7 - Prob. 50ECh. 2.7 - Prob. 51ECh. 2.7 - Prob. 52ECh. 2.7 - Prob. 53ECh. 2.7 - Prob. 54ECh. 2.7 - Prob. 55ECh. 2.7 - Prob. 56ECh. 2.7 - Prob. 57ECh. 2.7 - Prob. 58ECh. 2.7 - Prob. 59PSCh. 2.7 - Prob. 60PSCh. 2.7 - Prob. 61PSCh. 2.7 - Prob. 62PSCh. 2.7 - Prob. 63PSCh. 2.7 - Prob. 64PSCh. 2.7 - Prob. 65PSCh. 2.8 - Prob. 1GPCh. 2.8 - Prob. 2GPCh. 2.8 - Prob. 3GPCh. 2.8 - Prob. 4GPCh. 2.8 - Prob. 5GPCh. 2.8 - Prob. 1ECh. 2.8 - Prob. 2ECh. 2.8 - Prob. 3ECh. 2.8 - Prob. 4ECh. 2.8 - Prob. 5ECh. 2.8 - Prob. 6ECh. 2.8 - Prob. 7ECh. 2.8 - Prob. 8ECh. 2.8 - Prob. 9ECh. 2.8 - Prob. 10ECh. 2.8 - Prob. 11ECh. 2.8 - Prob. 12ECh. 2.8 - Prob. 13ECh. 2.8 - Prob. 14ECh. 2.8 - Prob. 15ECh. 2.8 - Prob. 16ECh. 2.8 - Prob. 17ECh. 2.8 - Prob. 18ECh. 2.8 - Prob. 19ECh. 2.8 - Prob. 20ECh. 2.8 - Prob. 21ECh. 2.8 - Prob. 22ECh. 2.8 - Prob. 23ECh. 2.8 - Prob. 24ECh. 2.8 - Prob. 25ECh. 2.8 - Prob. 26ECh. 2.8 - Prob. 27ECh. 2.8 - Prob. 28ECh. 2.8 - Prob. 29ECh. 2.8 - Prob. 30ECh. 2.8 - Prob. 31ECh. 2.8 - Prob. 32ECh. 2.8 - Prob. 33ECh. 2.8 - Prob. 34ECh. 2.8 - Prob. 35ECh. 2.8 - Prob. 36ECh. 2.8 - Prob. 37ECh. 2.8 - Prob. 38ECh. 2.8 - Prob. 39PSCh. 2.8 - Prob. 40PSCh. 2.8 - Prob. 41PSCh. 2.8 - Prob. 42PSCh. 2.8 - Prob. 43PSCh. 2.8 - Prob. 44PSCh. 2.8 - Prob. 1QCh. 2.8 - Prob. 2QCh. 2.8 - Prob. 3QCh. 2.8 - Prob. 4QCh. 2.8 - Prob. 5QCh. 2.8 - Prob. 6QCh. 2.8 - Prob. 7QCh. 2.8 - Prob. 8QCh. 2.8 - Prob. 9QCh. 2.8 - Prob. 10QCh. 2.8 - Prob. 1MRPSCh. 2.8 - Prob. 2MRPSCh. 2.8 - Prob. 3MRPSCh. 2.8 - Prob. 4MRPSCh. 2.8 - Prob. 5MRPSCh. 2.8 - Prob. 6MRPSCh. 2.8 - Prob. 7MRPSCh. 2 - Prob. 1VECh. 2 - Prob. 2VECh. 2 - Prob. 3VECh. 2 - Prob. 4VECh. 2 - Prob. 5REAECh. 2 - Prob. 6REAECh. 2 - Prob. 7REAECh. 2 - Prob. 8REAECh. 2 - Prob. 9REAECh. 2 - Prob. 10REAECh. 2 - Prob. 11REAECh. 2 - Prob. 12REAECh. 2 - Prob. 13REAECh. 2 - Prob. 14REAECh. 2 - Prob. 15REAECh. 2 - Prob. 16REAECh. 2 - Prob. 17REAECh. 2 - Prob. 18REAECh. 2 - Prob. 19REAECh. 2 - Prob. 20REAECh. 2 - Prob. 21REAECh. 2 - Prob. 22REAECh. 2 - Prob. 23REAECh. 2 - Prob. 24REAECh. 2 - Prob. 25REAECh. 2 - Prob. 26REAECh. 2 - Prob. 27REAECh. 2 - Prob. 28REAECh. 2 - Prob. 29REAECh. 2 - Prob. 30REAECh. 2 - Prob. 31REAECh. 2 - Prob. 32REAECh. 2 - Prob. 33REAECh. 2 - Prob. 34REAECh. 2 - Prob. 35REAECh. 2 - Prob. 36REAECh. 2 - Prob. 37REAECh. 2 - Prob. 38REAECh. 2 - Prob. 39REAECh. 2 - Prob. 40REAECh. 2 - Prob. 1TCh. 2 - Prob. 2TCh. 2 - Prob. 3TCh. 2 - Prob. 4TCh. 2 - Prob. 5TCh. 2 - Prob. 6TCh. 2 - Prob. 7TCh. 2 - Prob. 8TCh. 2 - Prob. 9TCh. 2 - Prob. 10TCh. 2 - Prob. 11TCh. 2 - Prob. 12TCh. 2 - Prob. 13TCh. 2 - Prob. 14TCh. 2 - Prob. 15TCh. 2 - Prob. 16TCh. 2 - Prob. 17TCh. 2 - Prob. 18TCh. 2 - Prob. 19TCh. 2 - Prob. 20TCh. 2 - Prob. 21TCh. 2 - Prob. 22TCh. 2 - Prob. 23TCh. 2 - Prob. 24TCh. 2 - Prob. 25TCh. 2 - Prob. 26TCh. 2 - Prob. 27TCh. 2 - Prob. 28TCh. 2 - Prob. 29TCh. 2 - Prob. 1PCh. 2 - Prob. 2PCh. 2 - Prob. 1TPCh. 2 - Prob. 2TPCh. 2 - Prob. 3TPCh. 2 - Prob. 4TPCh. 2 - Prob. 5TPCh. 2 - Prob. 6TPCh. 2 - Prob. 7TPCh. 2 - Prob. 8TPCh. 2 - Prob. 9TPCh. 2 - Prob. 10TPCh. 2 - Prob. 11TPCh. 2 - Prob. 12TPCh. 2 - Prob. 13TPCh. 2 - Prob. 14TPCh. 2 - Prob. 15TPCh. 2 - Prob. 16TPCh. 2 - Prob. 17TPCh. 2 - Prob. 18TPCh. 2 - Prob. 19TPCh. 2 - Prob. 20TPCh. 2 - Prob. 21TP
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, algebra and related others by exploring similar questions and additional content below.Similar questions
- Please use the infinite series formula and specify how you did each step. Thank you.arrow_forward8) Solve the given system using the Gaussian Elimination process. 2x8y = 3 (-6x+24y = −6arrow_forward7) Solve the given system using the Gaussian Elimination process. (5x-4y = 34 (2x - 2y = 14arrow_forward
- 33 (a) (b) Let A(t) = = et 0 0 0 cos(t) sin(t) 0-sin(t) cos(t)) For any fixed tЄR, find det(A(t)). Show that the matrix A(t) is invertible for any tЄ R, and find the inverse (A(t))¹.arrow_forwardUse the infinite geometric sum to convert .258 (the 58 is recurring, so there is a bar over it) to a ratio of two integers. Please go over the full problem, specifying how you found r. Thank you.arrow_forwardH.w: Find the Eigen vectors for the largest Eigen value of the system X1+ +2x3=0 3x1-2x2+x3=0 4x1+ +3x3=0arrow_forward
- need help with 5 and 6 pleasearrow_forward1) Given matrix A below, answer the following questions: a) What is the order of the matrix? b) What is the element a13? c) What is the element a₁₁? 4 -1arrow_forward[25 points] Given the vector let v = ER² and the collection of vectors ε = E-{)·()}-{☹) (9)} = {(A)·(9)}· B: = and C = · {(6)·(})}· answer the following question. (a) (b) (c) (d) (e) verify Verify is a basis for R² and find the coordinate [] of under ε. Verify B is a basis for R2 and find the coordinate []B of ʊ Verify C is a basis for R2 and find the coordinate []c of under ε. under ε. Find the change-of-basis matrix [I]+B from basis B to basis ε, and EE+BUB Find the change-of-basis matrix [I]B+ε from basis Ɛ to basis B, and verify [U]B= [] B+EVEarrow_forward
- Explain the following terms | (a) linear span (b) dimension of vector space (c) linearly independent (d) linearly dependent (e) rank of matrix Aarrow_forward3. Let u = 3/5 √ = and = -4/5 -() Define V span{ū, }. (a) (b) (c) Show that {u, } is orthonormal and forms a basis for V. Explicitly compute Projy w. Explicitly give a non-zero vector in V+.arrow_forwardIs 1.1 0.65 -3.4 0.23 0.4 -0.44 a basis for R3? You must explain your answer 0arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Algebra and Trigonometry (6th Edition)AlgebraISBN:9780134463216Author:Robert F. BlitzerPublisher:PEARSON
Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON
Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press
College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education
Algebra and Trigonometry (6th Edition)
Algebra
ISBN:9780134463216
Author:Robert F. Blitzer
Publisher:PEARSON
Contemporary Abstract Algebra
Algebra
ISBN:9781305657960
Author:Joseph Gallian
Publisher:Cengage Learning
Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning
Algebra And Trigonometry (11th Edition)
Algebra
ISBN:9780135163078
Author:Michael Sullivan
Publisher:PEARSON
Introduction to Linear Algebra, Fifth Edition
Algebra
ISBN:9780980232776
Author:Gilbert Strang
Publisher:Wellesley-Cambridge Press
College Algebra (Collegiate Math)
Algebra
ISBN:9780077836344
Author:Julie Miller, Donna Gerken
Publisher:McGraw-Hill Education
2.1 Introduction to inequalities; Author: Oli Notes;https://www.youtube.com/watch?v=D6erN5YTlXE;License: Standard YouTube License, CC-BY
GCSE Maths - What are Inequalities? (Inequalities Part 1) #56; Author: Cognito;https://www.youtube.com/watch?v=e_tY6X5PwWw;License: Standard YouTube License, CC-BY
Introduction to Inequalities | Inequality Symbols | Testing Solutions for Inequalities; Author: Scam Squad Math;https://www.youtube.com/watch?v=paZSN7sV1R8;License: Standard YouTube License, CC-BY