
Concept explainers
Explain what each of the following means and illustrate with sketch.
(a) limx→af(x)=L
(b) limx→a+f(x)=L
(c) limx→a−f(x)=L
(d) limx→af(x)=∞
(e) limx→∞f(x)=L
(a)
To explain: The meaning of limx→af(x)=L.
Explanation of Solution
Result used:
Definition of limit:
Let f(x) be a function is defined when x approaches to p then limx→pf(x)=L, if for every number ε>0 there is some δ>0 such that |f(x)−L|<ε whenever 0<|x−p|<δ.
Graph:
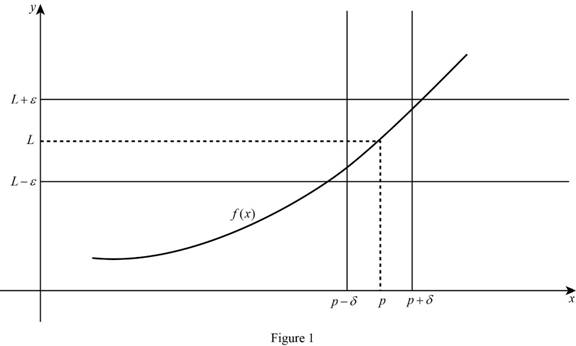
Calculation:
The limit of the function limx→af(x)=L means the limit of f(x) equal to L when x approaches to a, if x is closer and closer to a from the both sides then the value of f(x) also closer and closer to L.
In the limit definition x≠a this means finding the limit of f(x) when x approaches to a, there no need to consider x=a.
There are three cases for define limx→af(x)=L.
Case (1):
The limit of the function limx→af(x)=L, if x approaches to a then the value of f(x) are closer to L and f(a) is L.
Graph:
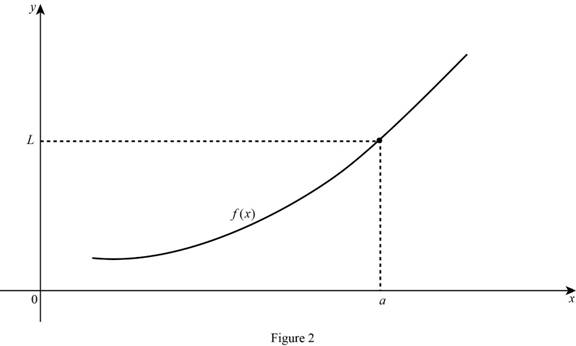
Case (2):
The limit of the function limx→af(x)=L, if x approaches to a then the value of f(x) are closer to L and f(a) is undefined.
Case (3):
The limit of the function limx→af(x)=L, if x approaches to a then the value of f(x) are closer to other than L.
Graph:
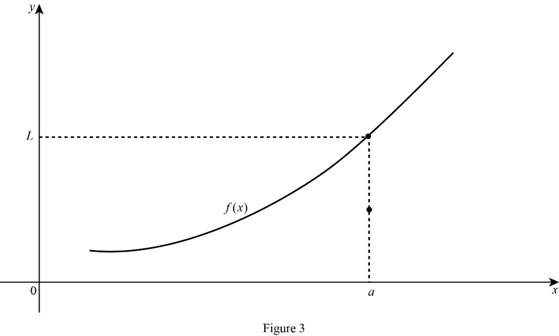
(b)
To explain: The meaning of limx→a+f(x)=L.
Explanation of Solution
Result used:
Definition of limit:
Let f(x) be a function is defined when x approaches to p then limx→pf(x)=L, if for every number ε>0 there is some δ>0 such that |f(x)−L|<ε whenever 0<|x−p|<δ.
Calculation:
limx→a+f(x)=L means the limit of f(x) equal to L when x approaches to a from the right, if x is closer and closer to a from the right and remains greater than a then the value of f(x) also closer and closer to L.
Graph:
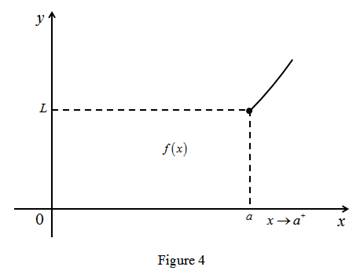
(c)
To explain: The meaning of limx→a−f(x)=L.
Explanation of Solution
Result used:
Definition of limit:
Let f(x) be a function is defined when x approaches to p then limx→pf(x)=L, if for every number ε>0 there is some δ>0 such that |f(x)−L|<ε whenever 0<|x−p|<δ.
Calculation:
The limit of the function limx→a−f(x)=L means the limit of f(x) equal to L when x approaches to a from the left, if x is closer and closer to a from the left and remains less than a then the value of f(x) also closer and closer to L.
Graph:
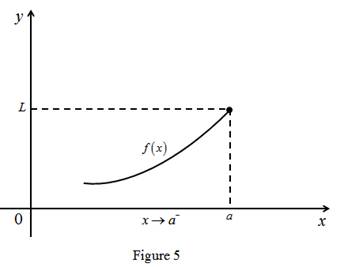
(d)
To explain: The meaning of limx→af(x)=∞.
Explanation of Solution
Result used:
Definition of limit:
Let f(x) be a function is defined when x approaches to p then limx→pf(x)=L, if for every number ε>0 there is some δ>0 such that |f(x)−L|<ε whenever 0<|x−p|<δ.
Calculation:
The limit of the function limx→af(x)=∞ means the limit of f(x) is larger value when x approaches to a from the both sides. That is any M>0, f(x)>M for some x-value is sufficiently close to a.
Graph:
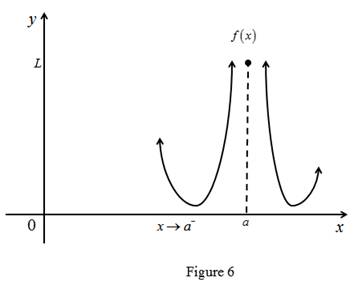
(e)
To explain: The meaning of limx→∞f(x)=L.
Explanation of Solution
Result used:
Definition of limit:
Let f(x) be a function is defined when x approaches to p then limx→pf(x)=L, if for every number ε>0 there is some δ>0 such that |f(x)−L|<ε whenever 0<|x−p|<δ.
Calculation:
The limit of the function limx→∞f(x)=L means the limit of f(x) is L when x approaches to larger value the graph get closer and closer to the line y=L.
Graph:
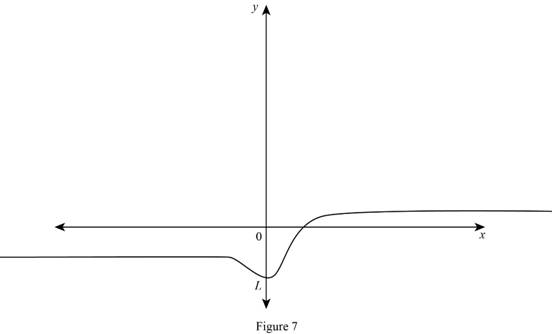
Want to see more full solutions like this?
Chapter 2 Solutions
Student Solutions Manual for Stewart's Single Variable Calculus: Early Transcendentals, 8th (James Stewart Calculus)
Additional Math Textbook Solutions
Finite Mathematics for Business, Economics, Life Sciences and Social Sciences
Calculus: Early Transcendentals (2nd Edition)
Mathematics for the Trades: A Guided Approach (11th Edition) (What's New in Trade Math)
A First Course in Probability (10th Edition)
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
- This question builds on an earlier problem. The randomized numbers may have changed, but have your work for the previous problem available to help with this one. A 4-centimeter rod is attached at one end to a point A rotating counterclockwise on a wheel of radius 2 cm. The other end B is free to move back and forth along a horizontal bar that goes through the center of the wheel. At time t=0 the rod is situated as in the diagram at the left below. The wheel rotates counterclockwise at 1.5 rev/sec. At some point, the rod will be tangent to the circle as shown in the third picture. B A B at some instant, the piston will be tangent to the circle (a) Express the x and y coordinates of point A as functions of t: x= 2 cos(3πt) and y= 2 sin(3πt) (b) Write a formula for the slope of the tangent line to the circle at the point A at time t seconds: -cot (3πt) (c) Express the x-coordinate of the right end of the rod at point B as a function of t: 2 cos(3πt) +41/1 (d) Express the slope of the rod…arrow_forward4. [-/1 Points] DETAILS MY NOTES SESSCALCET2 6.5.024. Find the approximations Tη, Mn, and S, to the integral computer algebra system.) ASK YOUR TEACHER PRACTICE ANOTHER 4 39 √ dx for n = 6 and 12. Then compute the corresponding errors ET, EM, and Es. (Round your answers to six decimal places. You may wish to use the sum command on a n Tn Mn Sp 6 12 n ET EM Es 6 12 What observations can you make? In particular, what happens to the errors when n is doubled? As n is doubled, ET and EM are decreased by a factor of about Need Help? Read It ' and Es is decreased by a factor of aboutarrow_forward6. [-/1 Points] DETAILS MY NOTES SESSCALCET2 6.5.001. ASK YOUR TEACHER PRACTICE ANOTHER Let I = 4 f(x) dx, where f is the function whose graph is shown. = √ ² F(x 12 4 y f 1 2 (a) Use the graph to find L2, R2 and M2. 42 = R₂ = M₂ = 1 x 3 4arrow_forward
- practice problem please help!arrow_forwardFind a parameterization for a circle of radius 4 with center (-4,-6,-3) in a plane parallel to the yz plane. Write your parameterization so the y component includes a positive cosine.arrow_forward~ exp(10). A 3. Claim number per policy is modelled by Poisson(A) with A sample x of N = 100 policies presents an average = 4 claims per policy. (i) Compute an a priory estimate of numbers of claims per policy. [2 Marks] (ii) Determine the posterior distribution of A. Give your argument. [5 Marks] (iii) Compute an a posteriori estimate of numbers of claims per policy. [3 Marks]arrow_forward
- 2. The size of a claim is modelled by F(a, λ) with a fixed a a maximum likelihood estimate of A given a sample x with a sample mean x = 11 = 121. Give [5 Marks]arrow_forwardRobbie Bearing Word Problems Angles name: Jocelyn date: 1/18 8K 2. A Delta airplane and an SouthWest airplane take off from an airport at the same time. The bearing from the airport to the Delta plane is 23° and the bearing to the SouthWest plane is 152°. Two hours later the Delta plane is 1,103 miles from the airport and the SouthWest plane is 1,156 miles from the airport. What is the distance between the two planes? What is the bearing from the Delta plane to the SouthWest plane? What is the bearing to the Delta plane from the SouthWest plane? Delta y SW Angles ThreeFourthsMe MATH 2arrow_forwardFind the derivative of the function. m(t) = -4t (6t7 - 1)6arrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





