Chapter 2, Problem 119P

(a)

To determine

To show:The speed of a sky diver, whose acceleration is given by the equation $a_y=g-b{v}_y^2$ is given by $v_y\left(t\right)=v_t\tanh \left(\frac{t}{T}\right)$ ,when expressed as a function of time, where $v_t$ is the terminal speed which is given by $v_t=\sqrt{\frac{g}{b}}$ and $T$ is the time scale parameter given by $T=\frac{v_t}{g}$ .

Explanation of Solution

Given:

The equation for the acceleration $a_y$ of the sky diver as a function of its speed $v_y$

  $a_y=g-b{v}_y^2$  ........(1)

The expressions for the terminal speed $v_t$ and the time scale parameter $T$ :

  $v_t=\sqrt{\frac{g}{b}}$  ........(2)

  $T=\frac{v_t}{g}$  ........(3)

The speed of the sky diver at time $t=0$

  ${\left(v_y\right)}_{t=0}=0$

Calculation:

Rewrite equation (1) using the expression for acceleration $a_y=\frac{d{v}_y}{dt}$ ,as follows:

  $\frac{d{v}_y}{dt}=g-b{v}_y^2$

Rearrange the above equation as follows:

  $\frac{d{v}_y}{g-b{v}_y^2}=dt$

Integrate both sides of the equation.

  ${\displaystyle \int \frac{d{v}_y}{g-b{v}_y^2}}={\displaystyle \int dt}$

Therefore,

  ${\displaystyle \int \frac{d{v}_y}{g-b{v}_y^2}}=t+C$  ........(4)

Evaluate the integral ${\displaystyle \int \frac{d{v}_y}{g-b{v}_y^2}}$ as shown below:

  $\begin{array}{c}{\displaystyle \int \frac{d{v}_y}{g-b{v}_y^2}}=\frac{1}{g}{\displaystyle \int \frac{d{v}_y}{1-\frac{b}{g}{v}_y^2}}\\ =\frac{1}{g}{\displaystyle \int \frac{d{v}_y}{1-{\left(\sqrt{\frac{b}{g}}{v}_y\right)}^2}}\end{array}$  ........(5)

Let $u=\sqrt{\frac{b}{g}}{v}_y$ .  ........(6)

Therefore,

  $\begin{array}{c}du=\sqrt{\frac{b}{g}}d{v}_y\\ d{v}_y=\sqrt{\frac{g}{b}}du\end{array}$

Rewrite equation (5) as shown:

  $\begin{array}{c}{\displaystyle \int \frac{d{v}_y}{g-b{v}_y^2}}=\frac{1}{g}{\displaystyle \int \frac{d{v}_y}{1-{\left(\sqrt{\frac{b}{g}}{v}_y\right)}^2}}\\ =\left(\frac{1}{g}\right)\left(\sqrt{\frac{g}{b}}\right){\displaystyle \int \frac{du}{1-u^2}}\\ =\frac{1}{\sqrt{gb}}{\displaystyle \int \frac{du}{1-u^2}}\end{array}$  ........(7)

The expression $\frac{1}{1-u^2}$ can be written as

  $\frac{1}{1-u^2}=\frac{1}{2}\left(\frac{1}{1+u}+\frac{1}{1-u}\right)$

Therefore, equation (7) takes the form,

  $\begin{array}{c}{\displaystyle \int \frac{d{v}_y}{g-b{v}_y^2}}=\frac{1}{\sqrt{gb}}{\displaystyle \int \frac{du}{1-u^2}}\\ =\frac{1}{\sqrt{gb}}{\displaystyle \int \frac{1}{2}\left(\frac{1}{1+u}+\frac{1}{1-u}\right)}du\\ =\frac{1}{2\sqrt{gb}}\left[\ln \left(1+u\right)-\ln \left(1-u\right)\right]\\ =\left(\frac{1}{\sqrt{gb}}\right)\left[\frac{1}{2}\ln \frac{1+u}{1-u}\right]\end{array}$  ........(8)

Use the identity,

  $\arctan \text{h }u=\frac{1}{2}\ln \frac{1+u}{1-u}$

Hence write equation (8) as,

  $\begin{array}{c}{\displaystyle \int \frac{d{v}_y}{g-b{v}_y^2}}=\left(\frac{1}{\sqrt{gb}}\right)\left[\frac{1}{2}\ln \frac{1+u}{1-u}\right]\\ =\left(\frac{1}{\sqrt{gb}}\right)\left(\arctan \text{h}u\right)\end{array}$

Therefore, equation (4) can be written as ,

  $\left(\frac{1}{\sqrt{gb}}\right)\left(\arctan \text{h}u\right)=t+C$  .....(9)

Substitute the value of $u$ in equation (9).

  $\left(\frac{1}{\sqrt{gb}}\right)\left(\arctan \text{h}\left(\sqrt{\frac{b}{g}}{v}_y\right)\right)=t+C$  ........(10)

Apply the initial conditions of the sky diver ${\left(v_y\right)}_{t=0}=0$ in equation (10).

  $\begin{array}{c}\left(\frac{1}{\sqrt{gb}}\right)\left(\arctan \text{h}\left(\sqrt{\frac{b}{g}}\times 0\right)\right)=0+C\\ C=0\end{array}$

Therefore, equation (10) can be written as,

  $\left(\frac{1}{\sqrt{gb}}\right)\left(\arctan \text{h}\left(\sqrt{\frac{b}{g}}{v}_y\right)\right)=t$  ........(11)

Therefore,

  $\text{arc}\tanh \left(\sqrt{\frac{b}{g}}{v}_y\right)=\sqrt{gb}t$

  $\tanh \left(\sqrt{gb}t\right)=\sqrt{\frac{b}{g}}{v}_y$  ........(12)

From equations (2) $v_t=\sqrt{\frac{g}{b}}$ and (3) $T=\frac{v_t}{g}$ ,

  $\begin{array}{c}T=\frac{v_t}{g}\\ =\left(\sqrt{\frac{g}{b}}\right)\left(\frac{1}{g}\right)\\ =\frac{1}{\sqrt{gb}}\end{array}$

Therefore, equation (12) can be written as,

  $\begin{array}{c}\tanh \left(\sqrt{gb}t\right)=\sqrt{\frac{b}{g}}{v}_y\\ \tanh \left(\frac{t}{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\sqrt{gb}$}\right.}\right)=\frac{v_y}{\sqrt{\raisebox{1ex}{$g$}\!\left/ \!\raisebox{-1ex}{$b$}\right.}}\\ \tanh \left(\frac{t}{T}\right)=\frac{v_y}{v_t}\end{array}$

Hence,

  $v_y=v_t\tanh \left(\frac{t}{T}\right)$

Conclusion:

Thus, it is proved that the speed of a sky diver, whose acceleration is given by the equation $a_y=g-b{v}_y^2$ is given by $v_y\left(t\right)=v_t\tanh \left(\frac{t}{T}\right)$ .

(b)

To determine

To Find:The fraction of the terminal speed is the speed of the sky diver at time $t=T$ if $T$ is the time scale parameter given by $T=\frac{v_t}{g}$ .

Answer to Problem 119P

At time $t=T$ the speed of the sky diver is $0.762$ times the terminal speed.

Explanation of Solution

Given:

The equation for the speed of the sky diver

  $v_y=v_t\tanh \left(\frac{t}{T}\right)$

Calculation:

Substitute $t=T$ in the given equation:

  $\begin{array}{c}{v}_y=v_t\tanh \left(\frac{t}{T}\right)\\ =v_t\tanh \left(1\right)\\ =v_t\left(0.762\right)\end{array}$

Conclusion:

Thus, at time $t=T$ the speed of the sky diver is $0.762$ times the terminal speed.

(c)

To determine

To graph: $v_y$ as a function of time assuming the value of terminal velocity as $56\text{ m/s}$ .

Explanation of Solution

Given:

The equation for the speed of the sky diver

  $v_y=v_t\tanh \left(\frac{t}{T}\right)$

Calculation:

In a spread sheet, calculate the values of $v_y$ by substituting $56\text{ m/s}$ for $v_t$ and plot a graph of $v_y$ as a function of time as shown below:

  

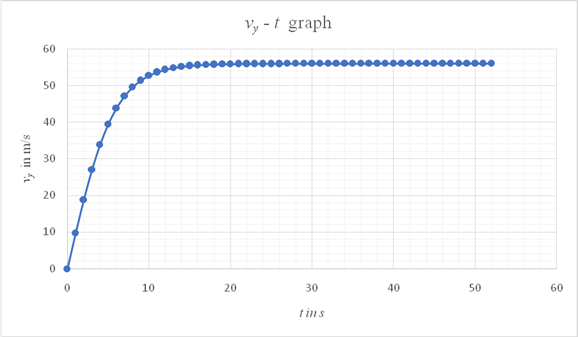
Conclusion:

Thus, it can be seen from the graph that the sky diver attains the terminal velocity at around 20 s.