
Concept explainers
A connecting rod is supported by a knife-edge at point A; the period of its small oscillations is observed to be 0.87 s. The rod is then inverted and supported by a knife edge at point B and the period of its small oscillations is observed to be 0.78 s. Knowing that ra + rb = 10 in., determine (a) the location of the mass center G, (b) the centroidal radius of gyration
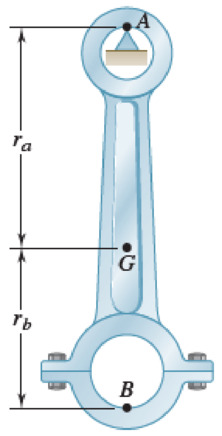
Fig. P19.47
(a)
The location
Answer to Problem 19.47P
The location
Explanation of Solution
Given information:
The period
The rod is then inverted and supported by a knife-edge at point B and the period
The value of
The acceleration due to gravity (g) is
Calculation:
Show the free body diagram of mass center G as in Figure (1).
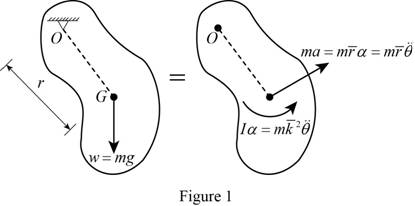
The external forces in the system are tension in the force due to the mass of the knife. The effective couple in the system is
Take moment about O in the system for external forces.
Take moment about O in the system for effective forces.
Equate the moment about O in the system for external and effective forces.
For small oscillation
Compare the differential Equation (1) with the general differential equation of motion
Write the expression for period
Substitute
Rewrite the equation (2) for rod suspended at A:
Rewrite the equation (2) for rod suspended at B:
Subtracting equation (4) from equation (3).
Substitute 0.87 s for
Write the relationship
Calculate the value
Substitute
Calculate the value
Substitute
Therefore, the location
(b)
The centroidal radius of gyration
Answer to Problem 19.47P
The centroidal radius of gyration
Explanation of Solution
Given information:
The period
The rod is then inverted and supported by a knife-edge at point B and the period
The value of
The acceleration due to gravity (g) is
Calculation:
Calculate the centroidal radius of gyration
Substitute
Therefore, the centroidal radius of gyration
Want to see more full solutions like this?
Chapter 19 Solutions
VECTOR MECHANIC
- A 1300-kg sports car has a center of gravity G located a distance h above a line connecting the front and rear axles. The car is suspended from cables that are attached to the front and rear axles as shown. Knowing that the periods of oscillation are 4.04 s when L = 4 m and 3.54 s when L = 3 m, determine h and the centroidal radius of gyration.arrow_forwardA 14-oz sphere A and a 10-oz sphere C are attached to the ends of a 20-oz rod AC are attached to the ends of a 20-oz rod B Determine the period of small oscillations of the rod.arrow_forwardA wheel is mounted on a steel shaft (G = 83×10° N/m²) of length (1.5 m) and radius (0.80 cm). The wheel is rotated (5°) and released. The period of oscillation is observed as (2.3 s). Determine the mass moment of inertia of the wheel. LU 1.5 m 0 (1) G= 83 x 10' N/m² r = 8 mm Fig (5)arrow_forward
- A 14-oz sphere A and a 10-oz sphere C are attached to the ends of a rod AC of negligible weight that can rotate in a vertical plane about an axis at B. Determine the period of small oscillations of the rod.arrow_forwardTwo 40-g weights are attached at A and B to the rim of a 1.5-kg uniform disk of radius r = 100 mm. Determine the frequency of small oscillations when β = 60°.arrow_forwardAs shown in the Fig. 3, the CM of a cylinder of mass m and radius R is connected to the top of hoop of mass m by a spring. The spring constant is assumed to be known and it is denoted by k. At a given moment the system is slightly compressed and then suddenly released. After the release, both rigid objects roll without slipping. Determine the angular frequency of the resulting oscillation. It is assumed that the spring remains horizontal throughout the motion. Figure 3: Coupled Oscillatorarrow_forward
- Two uniform rods, each of mass m and length l, are welded together to form the T-shaped assembly shown. Determine the frequency of small oscillations of the assembly.arrow_forwardA uniform disk of radius r = 120 mm is welded at its center to two elastic rods of equal length with fixed ends at A and B. Knowing that the disk rotates through an 8° angle when a 500-mN.m couple is applied to the disk and that it oscillates with a period of 1.3 s when the couple is removed, determine (a) the mass of the disk, (b) the period of vibration if one of the rods is removed.arrow_forwardThe 20-lb rod AB is attached to two 8-lb disks as shown. Knowing that the disks roll without sliding, determine the frequency of small oscillations of the system.arrow_forward
- Α Ο CH B d PROBLEM 19.50 A small collar of mass 1 kg is rigidly attached to a 3-kg uniform rod of length L = 750 mm. Determine (a) the distance d to maximize the frequency of oscillation when the rod is given a small initial displacement, (b) the corresponding period of oscillation.arrow_forwardA homogeneous wire of length 2l is bent as shown and allowed to oscillate about a frictionless pin at B. Denoting by τ0 the period of small oscillations when β = 0, determine the angle β for which the period of small oscillations is 2rO.arrow_forwardAnswer the following regarding mass:arrow_forward
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





