
Concept explainers
a)
To solve: The linear programming problem and answer the given questions.
Introduction:
Linear programming:
Linear programming is a mathematical modelling method where a linear function is maximized or minimized taking into consideration the various constraints present in the problem. It is useful in making quantitative decisions in business planning.
a)
Explanation of Solution
Given information:
Calculation of coordinates for each constraint and objective function:
Constraint 1:
Constraint 2:
Objective function:
The problem is solved with iso-profit line method.
Graph:
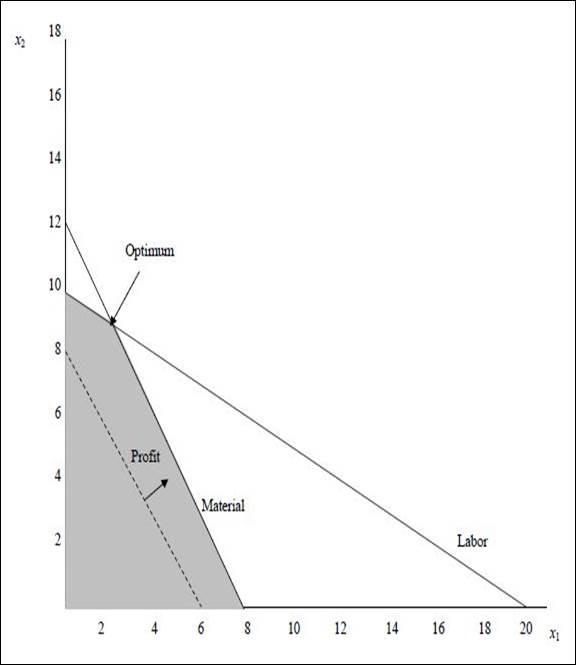
(1) Optimal value of the decision variables and Z:
The coordinates for the profit line is (6, 8). The profit line is moved away from the origin. The highest point at which the profit line intersects in the feasible region will be the optimum solution. The following equation are solved as simultaneous equation to find optimum solution.
Solving (1)and (2)we get,
The values are substituted in the objective function to find the objective function value.
Optimal solution:
(2)
None of the constraints are having slack. Both the ≤ constraints are binding.
(3)
There are no ≥ constraints. Hence, none of the constraints have surplus.
(4)
There are no redundant constraints.
b)
To solve: The linear programming problem and answer the questions.
Introduction:
Linear programming:
Linear programming is a mathematical modelling method where a linear function is maximized or minimized taking into consideration the various constraints present in the problem. It is useful in making quantitative decisions in business planning.
b)
Explanation of Solution
Given information:
Calculation of coordinates for each constraint and objective function:
Constraint 1:
Constraint 2:
Constraint 3:
Objective function:
The problem is solved with iso-profit line method.
Graph:
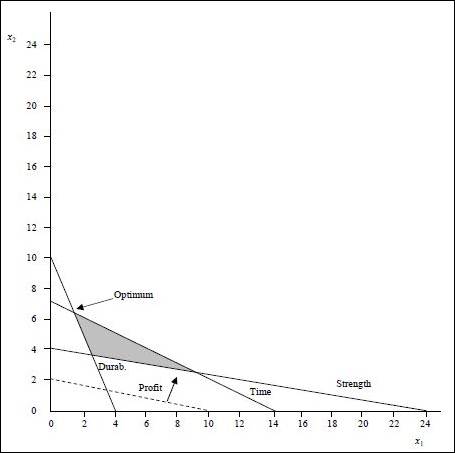
(1) Optimal value of the decision variables and Z:
The coordinates for the profit line is (10, 2). The profit line is moved away from the origin. The highest point at which the profit line intersects in the feasible region will be the optimum solution. The following equations are solved as simultaneous equation to find optimum solution.
Solving (1)and (2)we get,
The values are substituted in the objective function to find the objective function value.
Optimal solution:
(2)
None of the constraints are having slack. The time constraint has ≤ and it is binding.
(3)
Durability and strength constraints have ≥ in them. The durability constraint is binding and has no surplus. The strength constraint has surplus as shown below:
The surplus is 15 (39 -24).
(4)
There are no redundant constraints.
c)
To solve: The linear programming problem and answer the questions.
Introduction:
Linear programming:
Linear programming is a mathematical modelling method where a linear function is maximized or minimized taking into consideration the various constraints present in the problem. It is useful in making quantitative decisions in business planning.
c)
Explanation of Solution
Given information:
Calculation of coordinates for each constraint and objective function:
Constraint 1:
Constraint 2:
Constraint 3:
Objective function:
The problem is solved with iso-profit line method.
Graph:
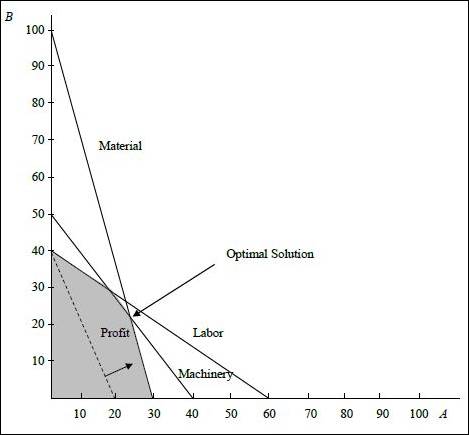
(1) Optimal value of the decision variables and Z:
The coordinates for the profit line is (20, 40). The profit line is moved away from the origin. The highest point at which the profit line intersects in the feasible region will be the optimum solution. The following equation are solved as simultaneous equation to find optimum solution.
Solving (1) and (2) we get,
The values are substituted in the objective function to find the objective function value.
Optimal solution:
(2)
The material and machinery constraint has ≤ and it is binding and has zero slack. The labor constraint has slack as shown below:
The slack is 120 (1,200 – 1,080).
(3)
There are no constraints with ≥. Hence, no constraints have surplus.
(4)
There are no redundant constraints
Want to see more full solutions like this?
Chapter 19 Solutions
Operations Management (Comp. Instructor's Edition)
- PepsiCo South Africa says the incident where a woman discovered part of a rodent in her loaf of bread, is anisolated occurrence.Durban woman, Nombulelo Mkumla, took to social media last week to share how she discovered the rodent.In a lengthy Facebook post, she said she purchased the loaf of bread from a local shop after work on August 27.For the next days, Mkumla proceeded to use slices of bread from the load to make toast."Then, on the morning of August 31, I took the bread out of the fridge to make toast and noticed something disgusting andscary. I took a picture and sent it to my friends, and one of them said, 'Yi mpuku leyo tshomi' [That's a rat friend]“."I was in denial and suggested it might be something else, but the rat scenario made sense - it's possible the rat got into thebread at the factory, and no one noticed," Mkumla said.She went back to the shop she'd bought the bread from and was told to lay a complaint directly with the supplier.She sent an email with a video and…arrow_forwardDurban woman, Nombulelo Mkumla, took to social media last week to share how she discovered the rodent.In a lengthy Facebook post, she said she purchased the loaf of bread from a local shop after work on August 27.For the next days, Mkumla proceeded to use slices of bread from the load to make toast."Then, on the morning of August 31, I took the bread out of the fridge to make toast and noticed something disgusting andscary. I took a picture and sent it to my friends, and one of them said, 'Yi mpuku leyo tshomi' [That's a rat friend]“."I was in denial and suggested it might be something else, but the rat scenario made sense - it's possible the rat got into thebread at the factory, and no one noticed," Mkumla said.She went back to the shop she'd bought the bread from and was told to lay a complaint directly with the supplier.She sent an email with a video and photographs of the bread.Mkumla said she was later contacted by a man from Sasko who apologised for the incident.According to…arrow_forwardRead the project statement and answer ALL of the questions that follow PROJECT STATEMENT The African Integrated High-Speed Railway Network (AIHSRN). African nations are preparing to invest billions in a significant overhaul of their rail infrastructure as part of an ambitious plan for the continent. One of the key projects underway is the African Integrated High-Speed Railway Network (AIHSRN), which aims to connect Africa's capital cities and major commercial centres with a high-speed railway network to enhance continental trade and competition. This network will span 2,000 km (1,243 miles) and connect 60 cities, including Nairobi, Lagos, Cairo, and Dakar. It will improve access to essential markets, enhance economic cooperation, and encourage regional collaboration. The plan is poised to revolutionise intra-African trade by reducing travel times and lowering transportation costs, making trade between African nations more competitive. The trains will be capable of reaching speeds of up…arrow_forward
- In the Sally Soprano case, Sally's agent prepares the potential issues to be discussed before the negotiation. Which items) may be on the list? Sally's salary and publicity Work-related benefits and incentives such as a hotel suite accommodation, limousine transportation, flower arrangements in the dressing room Future contracts and collaboration Rehearsal setup and arrangements All of the choicesarrow_forwardSummarize chapters 1 through 8 of the book "food and beverage cost control"arrow_forwardCan you guys help me with this? Thank you! Here's the question: Compared to the CONSTRAINT model, how has the network changed? How do you plan to add contingency to your network? Please answer this thoroughly Here's the what-if scenario: Assume that the LA warehouse becomes temporarily or even indefinitely disabled since facing a large-scale labor disruption. Re-optimize the network considering this new constraint. Here's the scenario comparison analysis: Scenario Constraint Scenario vs What-if Scenario Summary The Constraint Scenario exhibits a higher total cost of $7,424,575.45 compared to the What-if Scenario's total cost of $6,611,905.60, signifying a difference of approximately $812,669.85, which indicates a more expensive operation in the Constraint Scenario. The average service time is slightly higher in the Constraint Scenario (0.72 days vs. 0.70 days), suggesting that the What-if Scenario provides a marginally quicker service. Moreover, the average end-to-end service time…arrow_forward
- Can you guys help me with this? Thank you! Here's the question: Compared to the CONSTRAINT model, how has the network changed? How do you plan to add contingency to your network? Please answer this throughly Here's the what-if scenario: Assume that Dallas plant has lost power. It cannot serve the DCs anymore and has to remain locked indefinitely. Re-optimize the network considering this new constraint. Here's the scenario comparison analysis: Scenario Constraint Scenario vs What-if Scenario Summary In comparing the Constraint Scenario to the What-if Scenario, a few key differences highlight the efficiencies evident in the supply chain. Firstly, the total cost in the Constraint Scenario is lower at $7,424,575.45, while the What-if Scenario incurs a total cost of $7,486,369.12, resulting in a cost delta of $61,793.67. Additionally, although both scenarios exhibit the same average service time of 0.72 days, the What-if Scenario has a more favorable average end-to-end service time of 2.41…arrow_forwardEmployee In-Service Training ASSIGNMENT: In-Service Training. The intern is required to plan and implement two in-service training sessions for employees. Each in-service should last at least 10 but not more than 30 minutes and should be given to all employees affected. The preceptor or supervisor/unit manager must approve all in-service topics. 1) One presentation should be related to a policy or procedure of any kind (e.g. proper use of equipment); 2) The second presentation must be related to sanitation or safety. For each in-service presentation, the intern must develop a written class plan and a visual aid (may be a handout, poster, PowerPoint slide presentation, etc.) appropriate to the life experiences, cultural diversity and educational background of the target audience. The intern must also measure behavior change. Note, this cannot be measured by a written pre- and post- test. That would be measuring knowledge. The intern mustactually observe and document that the learners…arrow_forwardFor a dietary manager in a nursing home to train a dietary aidearrow_forward
 Practical Management ScienceOperations ManagementISBN:9781337406659Author:WINSTON, Wayne L.Publisher:Cengage,
Practical Management ScienceOperations ManagementISBN:9781337406659Author:WINSTON, Wayne L.Publisher:Cengage,
