Chapter 19, Problem 1P

a)

Summary Introduction

To solve: The linear programming problem and answer the given questions.

Introduction:

Linear programming:

Linear programming is a mathematical modelling method where a linear function is maximized or minimized taking into consideration the various constraints present in the problem. It is useful in making quantitative decisions in business planning.

Explanation of Solution

Given information:

$\begin{array}{c}MaximizeZ=4x_1+3x_2\\ Subjectto:\\ 6x_1+4x_2\le 48lb\left(Material\right)\\ 4x_1+8x_2\le 80hr\left(Labor\right)\\ x_1,x_2\ge 0\left(Non-negativity\right)\end{array}$

Calculation of coordinates for each constraint and objective function:

Constraint 1:

$6x_1+4x_2\le 48lb\left(Material\right)$

$\text{Substituting }{x}_1=0\text{ to find }{x}_2\text{,}$

$\begin{array}{c}6\left(0\right)+4x_2=48\\ 4x_2=48\\ x_2=\frac{48}{4}\\ x_2=12\end{array}$

$\text{Substituting }{x}_2=0\text{ to find }{x}_1\text{,}$

$\begin{array}{c}6x_1+4\left(0\right)=48\\ 6x_1=48\\ x_1=\frac{48}{6}\\ x_1=8\end{array}$

Constraint 2:

$4x_1+8x_2\le 80hr\left(Labor\right)$

$\text{Substituting }{x}_1=0\text{ to find }{x}_2\text{,}$

$\begin{array}{c}4\left(0\right)+8x_2=80\\ 8x_2=80\\ x_2=\frac{80}{8}\\ x_2=10\end{array}$

$\text{Substituting }{x}_2=0\text{ to find }{x}_1\text{,}$

$\begin{array}{c}4x_1+8\left(0\right)=80\\ 4x_1=80\\ x_1=\frac{80}{4}\\ x_1=20\end{array}$

Objective function:

The problem is solved with iso-profit line method.

$\text{Let }4x_1+3x_2=24$

$\text{Substituting }{x}_1=0\text{ to find }{x}_2\text{,}$

$\begin{array}{c}4\left(0\right)+3x_2=24\\ 3x_2=24\\ x_2=\frac{24}{3}\\ x_2=8\end{array}$

$\text{Substituting }{x}_2=0\text{ to find }{x}_1\text{,}$

$\begin{array}{c}4x_1+3\left(0\right)=24\\ 4x_1=24\\ x_1=\frac{24}{4}\\ x_1=6\end{array}$

Graph:

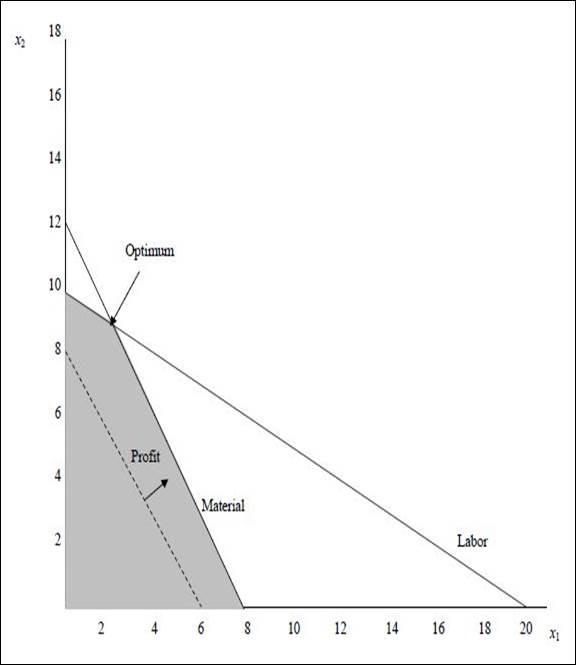
(1) Optimal value of the decision variables and Z:

The coordinates for the profit line is (6, 8). The profit line is moved away from the origin. The highest point at which the profit line intersects in the feasible region will be the optimum solution. The following equation are solved as simultaneous equation to find optimum solution.

$6x_1+4x_2=48$ (1)

$4x_1+8x_2=80$ (2)

Solving (1)and (2)we get,

$x_1=2,x_2=9$

The values are substituted in the objective function to find the objective function value.

$\begin{array}{c}MaximizeZ=4\left(2\right)+3\left(9\right)\\ =8+27\\ =35\end{array}$

Optimal solution:

$\begin{array}{l}{x}_1=2\\ x_2=9\\ Z=35\end{array}$

(2)

None of the constraints are having slack. Both the ≤ constraints are binding.

(3)

There are no ≥ constraints. Hence, none of the constraints have surplus.

(4)

There are no redundant constraints.

b)

Summary Introduction

To solve: The linear programming problem and answer the questions.

Introduction:

Linear programming:

Linear programming is a mathematical modelling method where a linear function is maximized or minimized taking into consideration the various constraints present in the problem. It is useful in making quantitative decisions in business planning.

Explanation of Solution

Given information:

$\begin{array}{c}MaximizeZ=2x_1+10x_2\\ Subjectto:\\ 10x_1+4x_2\ge 40wk\left(Durability\right)\\ x_1+6x_2\ge 24psi\left(Strength\right)\\ x_1+2x_2\ge 14hr\left(Time\right)\\ x_1,x_2\ge 0\left(Non-negativity\right)\end{array}$

Calculation of coordinates for each constraint and objective function:

Constraint 1:

$10x_1+4x_2\ge 40wk\left(Durability\right)$

$\text{Substituting }{x}_1=0\text{ to find }{x}_2\text{,}$

$\begin{array}{c}10\left(0\right)+4x_2=40\\ 4x_2=40\\ x_2=\frac{40}{4}\\ x_2=10\end{array}$

$\text{Substituting }{x}_2=0\text{ to find }{x}_1\text{,}$

$\begin{array}{c}10x_1+4\left(0\right)=40\\ 10x_1=40\\ x_1=\frac{40}{10}\\ x_1=4\end{array}$

Constraint 2:

$x_1+6x_2\ge 24psi\left(Strength\right)$

$\text{Substituting }{x}_1=0\text{ to find }{x}_2\text{,}$

$\begin{array}{c}\left(0\right)+6x_2=24\\ 6x_2=24\\ x_2=\frac{24}{6}\\ x_2=4\end{array}$

$\text{Substituting }{x}_2=0\text{ to find }{x}_1\text{,}$

$\begin{array}{c}{x}_1+6\left(0\right)=24\\ x_1=24\\ x_1=\frac{24}{1}\\ x_1=24\end{array}$

Constraint 3:

$x_1+2x_2\ge 14hr\left(Time\right)$

$\text{Substituting }{x}_1=0\text{ to find }{x}_2\text{,}$

$\begin{array}{c}\left(0\right)+2x_2=14\\ 2x_2=14\\ x_2=\frac{14}{2}\\ x_2=7\end{array}$

$\text{Substituting }{x}_2=0\text{ to find }{x}_1\text{,}$

$\begin{array}{c}{x}_1+2\left(0\right)=14\\ x_1=14\\ x_1=\frac{14}{1}\\ x_1=14\end{array}$

Objective function:

The problem is solved with iso-profit line method.

$\text{Let }2x_1+10x_2=20$

$\text{Substituting }{x}_1=0\text{ to find }{x}_2\text{,}$

$\begin{array}{c}2\left(0\right)+10x_2=20\\ 10x_2=20\\ x_2=\frac{20}{10}\\ x_2=2\end{array}$

$\text{Substituting }{x}_2=0\text{ to find }{x}_1\text{,}$

$\begin{array}{c}2x_1+10\left(0\right)=20\\ 2x_1=20\\ x_1=\frac{20}{2}\\ x_1=10\end{array}$

Graph:

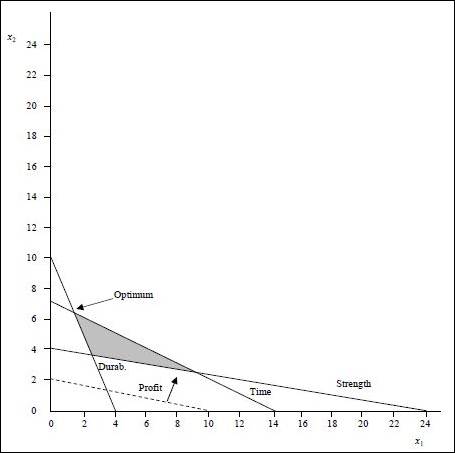
(1) Optimal value of the decision variables and Z:

The coordinates for the profit line is (10, 2). The profit line is moved away from the origin. The highest point at which the profit line intersects in the feasible region will be the optimum solution. The following equations are solved as simultaneous equation to find optimum solution.

$10x_1+4x_2=40$ (1)

$x_1+2x_2=14$ (2)

Solving (1)and (2)we get,

$x_1=1.5,x_2=6.25$

The values are substituted in the objective function to find the objective function value.

$\begin{array}{c}MaximizeZ=2\left(1.5\right)+10\left(6.25\right)\\ =3+62.5\\ =65.5\end{array}$

Optimal solution:

$\begin{array}{l}{x}_1=1.5\\ x_2=6.25\\ Z=65.5\end{array}$

(2)

None of the constraints are having slack. The time constraint has ≤ and it is binding.

(3)

Durability and strength constraints have ≥ in them. The durability constraint is binding and has no surplus. The strength constraint has surplus as shown below:

$\begin{array}{c}\left(1.5\right)+6\left(6.25\right)\ge 24\\ 1.5+37.5\ge 24\\ 39\ge 24\end{array}$

The surplus is 15 (39 -24).

(4)

There are no redundant constraints.

c)

Summary Introduction

To solve: The linear programming problem and answer the questions.

Introduction:

Linear programming:

Linear programming is a mathematical modelling method where a linear function is maximized or minimized taking into consideration the various constraints present in the problem. It is useful in making quantitative decisions in business planning.

Explanation of Solution

Given information:

$\begin{array}{c}MaximizeZ=6A+3B\\ Subjectto:\\ 20A+6B\le 600lb\left(Material\right)\\ 25A+20B\le 1,000hr\left(Machinery\right)\\ 20A+30B\le 1,200\left(Labor\right)\\ A,B\ge 0\left(Non-negativity\right)\end{array}$

Calculation of coordinates for each constraint and objective function:

Constraint 1:

$20A+6B\le 600lb\left(Material\right)$

$\text{Substituting }A=0\text{ to find }B\text{,}$

$\begin{array}{c}20\left(0\right)+6B=600\\ 6B=600\\ B=\frac{600}{6}\\ B=100\end{array}$

$\text{Substituting }B=0\text{ to find }A\text{,}$

$\begin{array}{c}20A+6\left(0\right)=600\\ 20A=600\\ A=\frac{600}{20}\\ A=30\end{array}$

Constraint 2:

$25A+20B\le 1,000hr\left(Machinery\right)$

$\text{Substituting }A=0\text{ to find }B\text{,}$

$\begin{array}{c}25\left(0\right)+20B=1,000\\ 20B=1,000\\ B=\frac{1,000}{20}\\ B=50\end{array}$

$\text{Substituting }B=0\text{ to find }A\text{,}$

$\begin{array}{c}25A+20\left(0\right)=1,000\\ 25A=1,000\\ A=\frac{1,000}{25}\\ A=40\end{array}$

Constraint 3:

$20A+30B\le 1,200$

$\text{Substituting }A=0\text{ to find }B\text{,}$

$\begin{array}{c}20\left(0\right)+30B=1,200\\ 30B=1,200\\ B=\frac{1,200}{30}\\ B=40\end{array}$

$\text{Substituting }B=0\text{ to find }A\text{,}$

$\begin{array}{c}20A+30\left(0\right)=1,200\\ 20A=1,200\\ A=\frac{1,200}{20}\\ A=60\end{array}$

Objective function:

The problem is solved with iso-profit line method.

$Let6A+3B=120$

$\text{Substituting }A=0\text{ to find }B\text{,}$

$\begin{array}{c}6\left(0\right)+3B=120\\ 3B=120\\ B=\frac{120}{3}\\ B=40\end{array}$

$\text{Substituting }B=0\text{ to find }A\text{,}$

$\begin{array}{c}6A+3\left(0\right)=120\\ 6A=120\\ A=\frac{120}{6}\\ A=20\end{array}$

Graph:

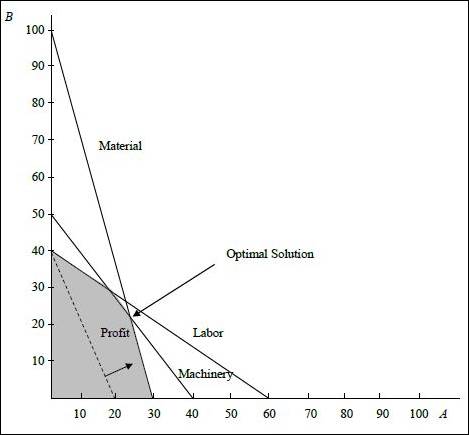
(1) Optimal value of the decision variables and Z:

The coordinates for the profit line is (20, 40). The profit line is moved away from the origin. The highest point at which the profit line intersects in the feasible region will be the optimum solution. The following equation are solved as simultaneous equation to find optimum solution.

$20A+6B=600$ (1)

$25A+20B=1,000$ (2)

Solving (1) and (2) we get,

$A=24,B=20$

The values are substituted in the objective function to find the objective function value.

$\begin{array}{c}MaximizeZ=6\left(24\right)+3\left(20\right)\\ =144+60\\ =204\end{array}$

Optimal solution:

$\begin{array}{l}A=24\\ B=20\\ Z=204\end{array}$

(2)

The material and machinery constraint has ≤ and it is binding and has zero slack. The labor constraint has slack as shown below:

$\begin{array}{c}20\left(24\right)+30\left(20\right)\le 1,200\\ 480+600\le 1,200\\ 1,080\le 1,200\end{array}$

The slack is 120 (1,200 – 1,080).

(3)

There are no constraints with ≥. Hence, no constraints have surplus.

(4)

There are no redundant constraints