
Concept explainers
a)
To solve: The linear programming problem and answer the given questions.
Introduction:
Linear programming:
Linear programming is a mathematical modelling method where a linear function is maximized or minimized taking into consideration the various constraints present in the problem. It is useful in making quantitative decisions in business planning.
a)
Explanation of Solution
Given information:
Calculation of coordinates for each constraint and objective function:
Constraint 1:
Constraint 2:
Objective function:
The problem is solved with iso-profit line method.
Graph:
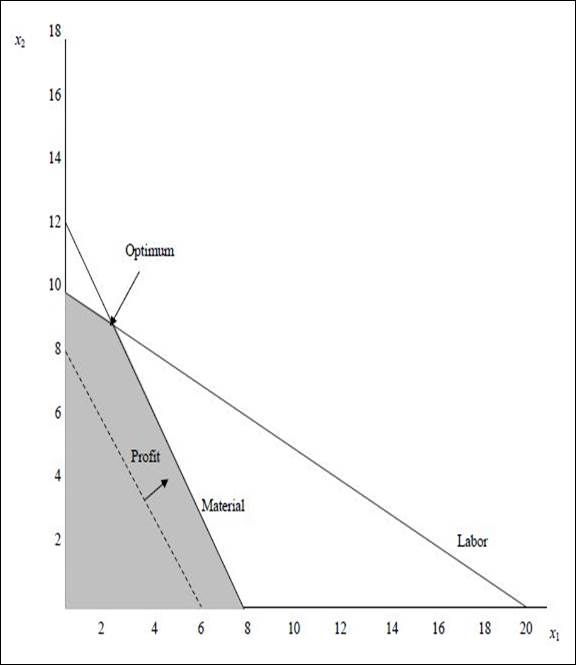
(1) Optimal value of the decision variables and Z:
The coordinates for the profit line is (6, 8). The profit line is moved away from the origin. The highest point at which the profit line intersects in the feasible region will be the optimum solution. The following equation are solved as simultaneous equation to find optimum solution.
Solving (1)and (2)we get,
The values are substituted in the objective function to find the objective function value.
Optimal solution:
(2)
None of the constraints are having slack. Both the ≤ constraints are binding.
(3)
There are no ≥ constraints. Hence, none of the constraints have surplus.
(4)
There are no redundant constraints.
b)
To solve: The linear programming problem and answer the questions.
Introduction:
Linear programming:
Linear programming is a mathematical modelling method where a linear function is maximized or minimized taking into consideration the various constraints present in the problem. It is useful in making quantitative decisions in business planning.
b)
Explanation of Solution
Given information:
Calculation of coordinates for each constraint and objective function:
Constraint 1:
Constraint 2:
Constraint 3:
Objective function:
The problem is solved with iso-profit line method.
Graph:
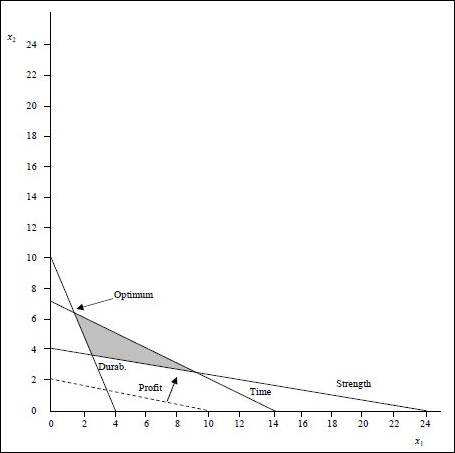
(1) Optimal value of the decision variables and Z:
The coordinates for the profit line is (10, 2). The profit line is moved away from the origin. The highest point at which the profit line intersects in the feasible region will be the optimum solution. The following equations are solved as simultaneous equation to find optimum solution.
Solving (1)and (2)we get,
The values are substituted in the objective function to find the objective function value.
Optimal solution:
(2)
None of the constraints are having slack. The time constraint has ≤ and it is binding.
(3)
Durability and strength constraints have ≥ in them. The durability constraint is binding and has no surplus. The strength constraint has surplus as shown below:
The surplus is 15 (39 -24).
(4)
There are no redundant constraints.
c)
To solve: The linear programming problem and answer the questions.
Introduction:
Linear programming:
Linear programming is a mathematical modelling method where a linear function is maximized or minimized taking into consideration the various constraints present in the problem. It is useful in making quantitative decisions in business planning.
c)
Explanation of Solution
Given information:
Calculation of coordinates for each constraint and objective function:
Constraint 1:
Constraint 2:
Constraint 3:
Objective function:
The problem is solved with iso-profit line method.
Graph:
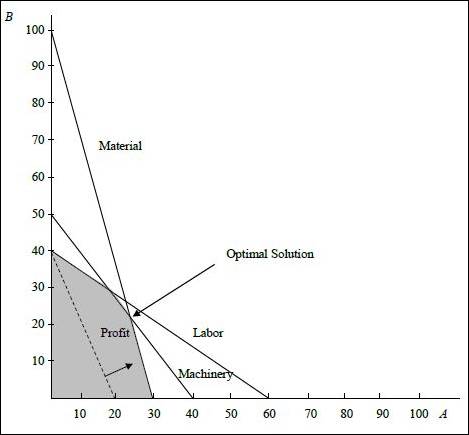
(1) Optimal value of the decision variables and Z:
The coordinates for the profit line is (20, 40). The profit line is moved away from the origin. The highest point at which the profit line intersects in the feasible region will be the optimum solution. The following equation are solved as simultaneous equation to find optimum solution.
Solving (1) and (2) we get,
The values are substituted in the objective function to find the objective function value.
Optimal solution:
(2)
The material and machinery constraint has ≤ and it is binding and has zero slack. The labor constraint has slack as shown below:
The slack is 120 (1,200 – 1,080).
(3)
There are no constraints with ≥. Hence, no constraints have surplus.
(4)
There are no redundant constraints
Want to see more full solutions like this?
Chapter 19 Solutions
Loose-leaf for Operations Management (The Mcgraw-hill Series in Operations and Decision Sciences)
- Yellow Press, Inc., buys paper in 1,500-pound rolls for printing. Annual demand is 2,250 rolls. The cost per roll is $625, and the annual holding cost is 20 percent of the cost. Each order costs $75. a. How many rolls should Yellow Press order at a time? Yellow Press should order rolls at a time. (Enter your response rounded to the nearest whole number.)arrow_forwardPlease help with only the one I circled! I solved the others :)arrow_forwardOsprey Sports stocks everything that a musky fisherman could want in the Great North Woods. A particular musky lure has been very popular with local fishermen as well as those who buy lures on the Internet from Osprey Sports. The cost to place orders with the supplier is $40/order; the demand averages 3 lures per day, with a standard deviation of 1 lure; and the inventory holding cost is $1.00/lure/year. The lead time form the supplier is 10 days, with a standard deviation of 2 days. It is important to maintain a 97 percent cycle-service level to properly balance service with inventory holding costs. Osprey Sports is open 350 days a year to allow the owners the opportunity to fish for muskies during the prime season. The owners want to use a continuous review inventory system for this item. Refer to the standard normal table for z-values. a. What order quantity should be used? lures. (Enter your response rounded to the nearest whole number.)arrow_forward
- In a P system, the lead time for a box of weed-killer is two weeks and the review period is one week. Demand during the protection interval averages 262 boxes, with a standard deviation of demand during the protection interval of 40 boxes. a. What is the cycle-service level when the target inventory is set at 350 boxes? Refer to the standard normal table as needed. The cycle-service level is ☐ %. (Enter your response rounded to two decimal places.)arrow_forwardOakwood Hospital is considering using ABC analysis to classify laboratory SKUs into three categories: those that will be delivered daily from their supplier (Class A items), those that will be controlled using a continuous review system (B items), and those that will be held in a two bin system (C items). The following table shows the annual dollar usage for a sample of eight SKUs. Fill in the blanks for annual dollar usage below. (Enter your responses rounded to the mearest whole number.) Annual SKU Unit Value Demand (units) Dollar Usage 1 $1.50 200 2 $0.02 120,000 $ 3 $1.00 40,000 $ 4 $0.02 1,200 5 $4.50 700 6 $0.20 60,000 7 $0.90 350 8 $0.45 80arrow_forwardA part is produced in lots of 1,000 units. It is assembled from 2 components worth $30 total. The value added in production (for labor and variable overhead) is $30 per unit, bringing total costs per completed unit to $60 The average lead time for the part is 7 weeks and annual demand is 3800 units, based on 50 business weeks per year. Part 2 a. How many units of the part are held, on average, in cycle inventory? enter your response here unitsarrow_forward
- assume the initial inventory has no holding cost in the first period and back orders are not permitted. Allocating production capacity to meet demand at a minimum cost using the transportation method. What is the total cost? ENTER your response is a whole number (answer is not $17,000. That was INCORRECT)arrow_forwardRegular Period Time Overtime Supply Available puewag Subcontract Forecast 40 15 15 40 2 35 40 28 15 15 20 15 22 65 60 Initial inventory Regular-time cost per unit Overtime cost per unit Subcontract cost per unit 20 units $100 $150 $200 Carrying cost per unit per month 84arrow_forwardassume that the initial inventory has no holding cost in the first period, and back orders are not permitted. Allocating production capacity to meet demand at a minimum cost using the transportation method. The total cost is? (enter as whole number)arrow_forward
- The S&OP team at Kansas Furniture, led by David Angelow, has received estimates of demand requirements as shown in the table. Assuming one-time stockout costs for lost sales of $125 per unit, inventory carrying costs of $30 per unit per month, and zero beginning and ending inventory, evaluate the following plan on an incremental cost basis: Plan B: Vary the workforce to produce the prior month's demand. Demand was 1,300 units in June. The cost of hiring additional workers is $35 per unit produced. The cost of layoffs is $60 per unit cut back. (Enter all responses as whole numbers.) Note: Both hiring and layoff costs are incurred in the month of the change (i.e., going from production of 1,300 in July to 1300 in August requires a layoff (and related costs) of 0 units in August). Hire Month 1 July Demand 1300 Production (Units) Layoff (Units) Ending Inventory Stockouts (Units) 2 August 1150 3 September 1100 4 October 1600 5 November 1900 6 December 1900arrow_forwardThe S&OP team at Kansas Furniture, led by David Angelow, has received estimates of demand requirements as shown in the table. Assuming one-time stockout costs for lost sales of $100 per unit, inventory carrying costs of $20 per unit per month, and zero beginning and ending inventory, evaluate the following plan on an incremental cost basis: Plan A: Produce at a steady rate (equal to minimum requirements) of 1,100 units per month and subcontract additional units at a $65 per unit premium cost. Subcontracting capacity is limited to 800 units per month. (Enter all responses as whole numbers). Ending Month Demand Production Inventory Subcontract (Units) 1 July 1300 1,100 0 2 August 1150 1,100 0 3 September 1100 1,100 0 4 October 1600 1,100 0 5 November 1900 1,100 0 6 December 1200 1,100 0arrow_forwardPlease help me expand upon my research even more in detail please. Need help added more to mine from the photos please. Not sure what more I can add.arrow_forward
 Practical Management ScienceOperations ManagementISBN:9781337406659Author:WINSTON, Wayne L.Publisher:Cengage,
Practical Management ScienceOperations ManagementISBN:9781337406659Author:WINSTON, Wayne L.Publisher:Cengage,
