
Review. A house roof is a perfectly flat plane that makes an angle θ with the horizontal. When its temperature changes, between Ti before dawn each day and Tk in the middle of each afternoon, the roof expands and contracts uniformly with a coefficient of thermal expansion α1. Resting on the roof is a flat, rectangular metal plate with expansion coefficient α2, greater than α1. The length of the plate is L, measured along the slope of the roof. The component of the plate’s weight perpendicular to the roof is supported by a normal force uniformly distributed over the area of the plate. The coefficient of kinetic friction between the plate and the roof is μk. The plate is always at the same temperature as the roof, so we assume its temperature is continuously changing. Because of the difference in expansion coefficients, each bit of the plate is moving relative to the roof below it, except for points along a certain horizontal line running across the plate called the stationary line. If the temperature is rising, parts of the plate below the stationary line are moving down relative to the roof and feel a force of kinetic friction acting up the roof. Elements of area above the stationary line are sliding up the roof, and on them kinetic friction acts downward parallel to the roof. The stationary line occupies no area, so we assume no force of static friction acts on the plate while the temperature is changing. The plate as a whole is very nearly in equilibrium, so the net
below the top edge of the plate. (b) Analyze the forces that act on the plate when the temperature is falling and prove that the stationary line is at that same distance above the bottom edge of the plate. (c) Show that the plate steps down the roof like an inchworm, moving each day by the distance
(d) Evaluate the distance an aluminum plate moves each day if its length is 1.20 m, the temperature cycles between 4.00°C and 36.0°C, and if the roof has slope 18.5°, coefficient of linear expansion 1.50 × 10−5 (°C) −1, and coefficient of friction 0.420 with the plate. (e) What If? What if the expansion coefficient of the plate is less than that of the roof? Will the plate creep up the roof?
(a)
To show: The stationary line is at distance of
Answer to Problem 19.78CP
Explanation of Solution
Given info: The angle made by the roof with the horizontal plane is
Consider the figure given below.
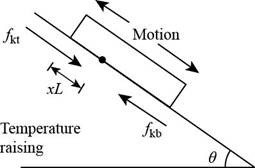
Figure 1
Consider that
The normal force on the lower part of the plane is,
Here,
The force due to gravity is,
The equation for the kinematic friction force is,
The equation for the downward force is,
The force equation for the plate is,
Further, solve for
The distance of the stationary line below the top edge is,
Conclusion:
Therefore, the distance at which stationary line lie is
(b)
To show: The stationary line is at that same distance above the bottom edge of the plate.
Answer to Problem 19.78CP
Explanation of Solution
Given info: The angle made by the roof with the horizontal plane is
Consider the figure given below.
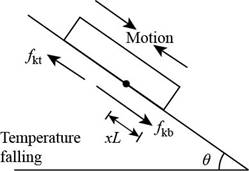
Figure 2
With the temperature falling, the plate contracts faster than the roof. The upper part slides down and feels an upward frictional force,
Then the force equation remains same as in part (a) and the stationary line is above the bottom edge by,
Conclusion:
Therefore, it is proved that the stationary line is at that same distance above the bottom edge of the plate.
(c)
To show: The plate steps down the roof like an inchworm moving each day by the distance
Answer to Problem 19.78CP
Explanation of Solution
Given info: The angle made by the roof with the horizontal plane is
Consider the figure given below.
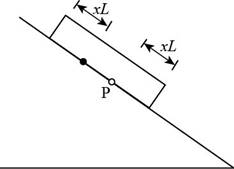
Figure 3
Consider the plate at dawn, as the temperature starts to rise. As in part (a), a line at distance
In the above figure, the point
The change in the length of the plate is,
The change in the length of the roof is,
The point on the roof originally under point
When the temperature drops, point
The displacement for a day is,
Substitute
Conclusion:
Therefore, the distance by which the plate steps down the roof like an inchworm moving each day is
(d)
Answer to Problem 19.78CP
Explanation of Solution
Given info: The angle made by the roof with the horizontal plane is
The length of the plate is
The coefficient of linear expansion for aluminum is
The formula for the displacement for a day is,
Substitute
Conclusion:
Therefore, the distance an aluminum plate moves each day is
(e)
To explain: The effect on the plate if the expansion coefficient of the plate is less than the expansion coefficient of the roof.
Answer to Problem 19.78CP
Explanation of Solution
Given info: The angle made by the roof with the horizontal plane is
If
The figure I, applies to the temperature falling and figure II applies to temperature rising. A point on the plate
The plate creeps down the roof each day by an amount given by,
Conclusion:
Therefore, the plate creeps down the roof each day by an amount given by
Want to see more full solutions like this?
Chapter 19 Solutions
Physics for Scientists and Engineers, Volume 1, Chapters 1-22
- Find the total capacitance in micro farads of the combination of capacitors shown in the figure below. 2.01 0.30 µF 2.5 µF 10 μF × HFarrow_forwardI do not understand the process to answer the second part of question b. Please help me understand how to get there!arrow_forwardRank the six combinations of electric charges on the basis of the electric force acting on 91. Define forces pointing to the right as positive and forces pointing to the left as negative. Rank in increasing order by placing the most negative on the left and the most positive on the right. To rank items as equivalent, overlap them. ▸ View Available Hint(s) [most negative 91 = +1nC 92 = +1nC 91 = -1nC 93 = +1nC 92- +1nC 93 = +1nC -1nC 92- -1nC 93- -1nC 91= +1nC 92 = +1nC 93=-1nC 91 +1nC 92=-1nC 93=-1nC 91 = +1nC 2 = −1nC 93 = +1nC The correct ranking cannot be determined. Reset Help most positivearrow_forward
- Part A Find the x-component of the electric field at the origin, point O. Express your answer in newtons per coulomb to three significant figures, keeping in mind that an x component that points to the right is positive. ▸ View Available Hint(s) Eoz = Η ΑΣΦ ? N/C Submit Part B Now, assume that charge q2 is negative; q2 = -6 nC, as shown in (Figure 2). What is the x-component of the net electric field at the origin, point O? Express your answer in newtons per coulomb to three significant figures, keeping in mind that an x component that points to the right is positive. ▸ View Available Hint(s) Eoz= Η ΑΣΦ ? N/Carrow_forward1. A charge of -25 μC is distributed uniformly throughout a spherical volume of radius 11.5 cm. Determine the electric field due to this charge at a distance of (a) 2 cm, (b) 4.6 cm, and (c) 25 cm from the center of the sphere. (a) = = (b) E = (c)Ẻ = = NC NC NCarrow_forward1. A long silver rod of radius 3.5 cm has a charge of -3.9 ис on its surface. Here ŕ is a unit vector ст directed perpendicularly away from the axis of the rod as shown in the figure. (a) Find the electric field at a point 5 cm from the center of the rod (an outside point). E = N C (b) Find the electric field at a point 1.8 cm from the center of the rod (an inside point) E=0 Think & Prepare N C 1. Is there a symmetry in the charge distribution? What kind of symmetry? 2. The problem gives the charge per unit length 1. How do you figure out the surface charge density σ from a?arrow_forward
- 1. Determine the electric flux through each surface whose cross-section is shown below. 55 S₂ -29 S5 SA S3 + 9 Enter your answer in terms of q and ε Φ (a) s₁ (b) s₂ = -29 (C) Φ զ Ερ (d) SA = (e) $5 (f) Sa $6 = II ✓ -29 S6 +39arrow_forwardNo chatgpt pls will upvotearrow_forwardthe cable may break and cause severe injury. cable is more likely to break as compared to the [1] ds, inclined at angles of 30° and 50° to the vertical rings by way of a scaled diagram. [4] I 30° T₁ 3cm 3.8T2 cm 200 N 50° at it is headed due North and its airspeed indicat 240 km/h. If there is a wind of 100 km/h from We e relative to the Earth? [3]arrow_forward
- Can you explain this using nodal analysis With the nodes I have present And then show me how many KCL equations I need to write, I’m thinking 2 since we have 2 dependent sourcesarrow_forwardstate the difference between vector and scalar quarrow_forwardPlease don't use Chatgpt will upvote and give handwritten solutionarrow_forward
 Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning





