Chapter 18.2, Problem 18.102P

(a)

To determine

The couple $M_0$.

Answer to Problem 18.102P

The couple $M_0$ is $\underset{\_}{\left(0.212\text{ft}\cdot \text{lb}\right)j}$.

Explanation of Solution

Given information:

The weight (W) of the disk is 6 lb.

The radius (r) of the disk is 3 in..

The angular velocity $\left({\omega }_1\right)$ of the disk is 60 rad/s.

The angular velocity of shaft CBD and arm AB $\left({\omega }_2\right)$ is 18 rad/s.

The horizontal distance (c) between the center of rod CBD and center of disk is 5 in..

The vertical distance (b) between the center of rod CBD and center of disk is 4 in..

The couple $\left(M_0\right)$ applied on the shaft is $0.25\text{ft}\cdot \text{lb}$.

The time (t) of couple applied is 3 s.

Calculation:

Find the mass (m) of the disk using the equation:

$m=\frac{W}{g}$

Here, g is the acceleration due to gravity.

Substitute 6 lb for W and $32.2{\text{ft/s}}^2$ for g.

$\begin{array}{c}m=\frac{6}{32.2}\\ =0.186335\text{lb}\cdot {\text{s}}^2\text{/ft}\end{array}$

Write the equation of vector form of angular velocity $\left(\Omega \right)$ of shaft CBD and AB.

$\Omega ={\omega }_{2}j$

The angular velocity $\left({\omega }_x\right)$ of disk A along the x-axis is zero.

Write the equation of angular velocity of disk A $\left({\omega }_y\right)$ along the y-axis:

${\omega }_y={\omega }_2$

Write the equation of angular velocity $\left({\omega }_z\right)$ of disk A along the z-axis:

${\omega }_z={\omega }_1$

Find the equation of angular velocity $\left(\omega \right)$ of disk.

$\omega ={\omega }_{x}i+{\omega }_{y}j+{\omega }_{z}k$

Substitute 0 for ${\omega }_x$, ${\omega }_2$ for ${\omega }_y$, and ${\omega }_1$ for ${\omega }_z$.

$\begin{array}{c}\omega =\left(0\right)i+\left({\omega }_2\right)j+\left({\omega }_1\right)k\\ ={\omega }_{2}j+{\omega }_{1}k\end{array}$

Find the equation of angular momentum about A $\left(H_A\right)$ about A.

$H_A={\overline{I}}_x{\omega }_{x}i+{\overline{I}}_y{\omega }_{y}j+{\overline{I}}_z{\omega }_{z}k$

Substitute 0 for ${\omega }_x$, ${\omega }_2$ for ${\omega }_y$, and ${\omega }_1$ for ${\omega }_z$.

$\begin{array}{c}{H}_A={\overline{I}}_x\left(0\right)i+{\overline{I}}_y{\omega }_{2}j+{\overline{I}}_z{\omega }_{1}k\\ ={\overline{I}}_y{\omega }_{2}j+{\overline{I}}_z{\omega }_{1}k\end{array}$ (1)

Find the rate of change of angular momentum ${\left({\dot{H}}_A\right)}_{Axyz}$ about the reference frame.

${\left({\dot{H}}_A\right)}_{Axyz}={\overline{I}}_y{\dot{\omega }}_{2}j+{\overline{I}}_z{\dot{\omega }}_{1}k$

Here, ${\dot{\omega }}_2$ is the acceleration of shaft CBD and arm and ${\dot{\omega }}_1$ is the angular acceleration disk.

Write the equation of the rate of change of angular momentum about A $\left({\dot{H}}_A\right)$.

$\left({\dot{H}}_A\right)={\left({\dot{H}}_A\right)}_{Axyz}+\Omega \times H_A$

Substitute ${\overline{I}}_y{\dot{\omega }}_{2}j+{\overline{I}}_z{\dot{\omega }}_{1}k$ for ${\left({\dot{H}}_A\right)}_{Axyz}$, ${\omega }_{2}j$ for $\Omega$, and ${\overline{I}}_y{\omega }_{2}j+{\overline{I}}_z{\omega }_{1}k$ for ${\dot{H}}_A$.

$\begin{array}{c}{\dot{H}}_A={\overline{I}}_y{\dot{\omega }}_{2}j+{\overline{I}}_z{\dot{\omega }}_{1}k+\left({\omega }_{2}j\right)\times \left[{\overline{I}}_y{\omega }_{2}j+{\overline{I}}_z{\omega }_{1}k\right]\\ ={\overline{I}}_y{\dot{\omega }}_{2}j+{\overline{I}}_z{\dot{\omega }}_{1}k+\left(0+{\overline{I}}_z{\omega }_1{\omega }_{2}i\right)\\ ={\overline{I}}_z{\omega }_1{\omega }_{2}i+{\overline{I}}_y{\dot{\omega }}_{2}j+{\overline{I}}_z{\dot{\omega }}_{1}k\end{array}$ (2)

Write the equation mass moment of inertia $\left({\overline{I}}_y\right)$ along y-axis.

${\overline{I}}_y=\frac{1}{4}m{r}^2$

Write the equation mass moment of inertia $\left({\overline{I}}_z\right)$ along y-axis.

${\overline{I}}_z=\frac{1}{2}m{r}^2$

Write the equation of velocity of the mass center A of the disk.

$\begin{array}{c}\overline{v}={\omega }_{2}j\times ci\\ =-c{\omega }_{2}k\end{array}$

Write the equation of acceleration of the mass center A of the disk.

$\overline{a}={\dot{\omega }}_{2}j\times ci+{\omega }_{2}j\times \overline{v}$

Substitute $-c{\omega }_{2}k$ for $\overline{v}$.

$\begin{array}{c}\overline{a}={\dot{\omega }}_{2}j\times ci+{\omega }_{2}j\times -c{\omega }_{2}k\\ =-c{\dot{\omega }}_{2}k-c{\omega }_2^{2}i\end{array}$

Find the position vector of D with respect to A.

$r_{AD}=ci+bj$

Substitute 5 in. for c and 4 in. for b.

$\begin{array}{c}{r}_{AD}=5\text{in}\text{.}\times \frac{1\text{ft}}{12\text{in}\text{.}}i+4\text{in}\text{.}\times \frac{1\text{ft}}{12\text{in}\text{.}}j\\ =0.41667i+0.33333j\end{array}$

Find the rate of change of angular momentum about D $\left({\dot{H}}_D\right)$.

${\dot{H}}_D={\dot{H}}_A+r_{AD}\times m\overline{a}$

Substitute ${\overline{I}}_z{\omega }_1{\omega }_{2}i+{\overline{I}}_y{\dot{\omega }}_{2}j+{\overline{I}}_z{\dot{\omega }}_{1}k$ for ${\dot{H}}_A$, $0.41667i+0.33333j$ for $r_{AD}$, and $-c{\dot{\omega }}_{2}k-c{\omega }_2^{2}i$ for $\overline{a}$.

$\begin{array}{c}{\dot{H}}_D=\left({\overline{I}}_z{\omega }_1{\omega }_{2}i+{\overline{I}}_y{\dot{\omega }}_{2}j+{\overline{I}}_z{\dot{\omega }}_{1}k\right)+\left(0.41667i+0.33333j\right)\times m\left(-c{\dot{\omega }}_{2}k-c{\omega }_2^{2}i\right)\\ =\left({\overline{I}}_z{\omega }_1{\omega }_{2}i+{\overline{I}}_y{\dot{\omega }}_{2}j+{\overline{I}}_z{\dot{\omega }}_{1}k\right)+0.41667mc{\dot{\omega }}_{2}j+0-0.33333mc{\dot{\omega }}_{2}i+0.33333mc{\omega }_2^{2}k\\ =\left({\overline{I}}_z{\omega }_1{\omega }_2-0.33333mc{\dot{\omega }}_2\right)i+\left({\overline{I}}_y+0.41667mc\right){\dot{\omega }}_{2}j+\left({\overline{I}}_z{\dot{\omega }}_1+0.33333mc{\omega }_2^2\right)k\end{array}$

Substitute $\frac{1}{2}m{r}^2$ for ${\overline{I}}_z$ and $\frac{1}{4}m{r}^2$ for ${\overline{I}}_y$.

$\begin{array}{c}{\dot{H}}_D=\left[\begin{array}{l}\left(\frac{1}{2}m{r}^2{\omega }_1{\omega }_2-0.33333mc{\dot{\omega }}_2\right)i+\left(\frac{1}{4}m{r}^2+0.41667mc\right){\dot{\omega }}_{2}j\\ +\left(\frac{1}{2}m{r}^2{\dot{\omega }}_1+0.33333mc{\omega }_2^2\right)k\end{array}\right]\\ =\left[\begin{array}{l}\left(\frac{1}{2}{r}^2{\omega }_1{\omega }_2-0.33333c{\dot{\omega }}_2\right)mi+\left(\frac{1}{4}{r}^2+0.41667c\right)m{\dot{\omega }}_{2}j\\ +\left(\frac{1}{2}{r}^2{\dot{\omega }}_1+0.33333c{\omega }_2^2\right)mk\end{array}\right]\end{array}$ (3)

Sketch the free body diagram and kinetic diagram of the system as shown in Figure (1).

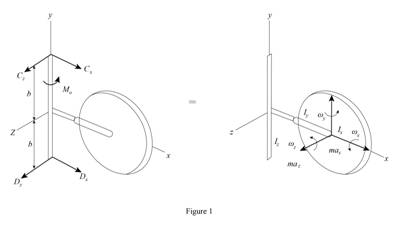
Refer Figure (1),

Apply Newton’s law of motion.

$\begin{array}{l}\Sigma F=m\overline{a}\\ C_{x}i+C_{y}k+D_{x}i+D_{z}k=m\overline{a}\end{array}$

Substitute $-c{\dot{\omega }}_{2}k-c{\omega }_2^{2}i$ for $\overline{a}$.

$C_{x}i+C_{y}k+D_{x}i+D_{z}k=m\left(-c{\dot{\omega }}_{2}k-c{\omega }_2^{2}i\right)$ (4)

Equate i-vector coefficients in Equation (3).

$C_x+D_x=-mc{\omega }_2^{2}i$ (5)

Equate k-vector coefficients in Equation (3).

$C_z+D_z=-mc{\dot{\omega }}_2$ (6)

Take moment about D.

$\begin{array}{c}\Sigma M_D=M_{0}j+2bj\times \left(C_{x}i+C_{z}k\right)\\ =M_{0}j-2b{C}_{x}k+2b{C}_{z}i\\ =2b{C}_{z}i+M_{0}j-2b{C}_{x}k\end{array}$ (7)

Here, $C_z$ is the dynamic reaction at C along z-axis, $M_0$ is the couple at O, and $C_x$ is the dynamic reaction at C along x-axis.

The moment at D is equal to the rate of change of angular momentum at D.

Equate Equation (3) and (7).

$2b{C}_{z}i+M_{0}j-2b{C}_{x}k=\left[\begin{array}{l}\left(\frac{1}{2}{r}^2{\omega }_1{\omega }_2-0.33333c{\dot{\omega }}_2\right)mi+\left(\frac{1}{4}{r}^2+0.41667c\right)m{\dot{\omega }}_{2}j\\ +\left(\frac{1}{2}{r}^2{\dot{\omega }}_1+0.33333c{\omega }_2^2\right)mk\end{array}\right]$ (8)

Find the angular acceleration $\left({\omega }_2\right)$ of shaft CBD and arm AB using the equation:

${\omega }_2={\left({\omega }_2\right)}_0+{\dot{\omega }}_{2}t$

Substitute 0 for ${\left({\omega }_2\right)}_0$, $18{\text{rad/s}}^2$ for ${\omega }_2$, and 3 s for t.

$\begin{array}{l}18=0+\left({\dot{\omega }}_2\right)\left(3\right)\\ {\dot{\omega }}_2=\frac{18}{3}\\ {\dot{\omega }}_2=6{\text{rad/s}}^2\end{array}$

Find the couple $M_0$ using equate the j- vector coefficients in Equation (8).

$M_0=\left(\frac{1}{4}{r}^2+0.41667c\right)m{\dot{\omega }}_2$

Substitute 3 in. for r, 5 in. for c, $0.186335\text{lb}\cdot {\text{s}}^2\text{/ft}$ for m, and $6{\text{rad/s}}^2$ for ${\dot{\omega }}_2$.

$\begin{array}{c}{M}_0=\left[\frac{1}{4}{\left(3\text{in}\text{.}\times \frac{1\text{ft}}{12\text{in}\text{.}}\right)}^2+0.41667\left(5\text{in}\text{.}\times \frac{1\text{ft}}{12\text{in}\text{.}}\right)\right]\left(0.186335\right){\dot{\omega }}_2\\ =\left(0.015625+0.17361\right)\left(0.186335\right)\left(6\right)\\ =\left(0.212\text{ft}\cdot \text{lb}\right)j\end{array}$

Thus, the couple $M_0$ is $\underset{\_}{\left(0.212\text{ft}\cdot \text{lb}\right)j}$.

(b)

To determine

The dynamic reaction at C and D after the couple has been removed.

Answer to Problem 18.102P

The dynamic reaction at C after the couple has been removed is $\underset{\_}{-\left(12.58\text{lb}\right)i+\left(9.43\text{lb}\right)k}$.

The dynamic reaction at D after the couple has been removed is $\underset{\_}{-\left(12.58\text{lb}\right)i-\left(9.43\text{lb}\right)k}$.

Explanation of Solution

Calculation:

After the 3 s, the couple $\left(M_0\right)$ is zero, the acceleration $\left({\dot{\omega }}_2\right)$ of shaft CBD and arm is zero.

Find the component of dynamic reaction at C $\left(C_x\right)$ along x-axis using equate the k- vector coefficients in Equation (8).

$-2b{C}_x=\left(\frac{1}{2}{r}^2{\dot{\omega }}_1+0.33333c{\omega }_2^2\right)m$ (9)

Substitute 4 in. for b, 3 in. for r, 5 in. for c, 18 rad/s for ${\omega }_2$ and $0.186335\text{lb}\cdot {\text{s}}^2\text{/ft}$ for m.

$\begin{array}{l}-2\left(4\text{in}\text{.}\times \frac{1\text{ft}}{12\text{in}\text{.}}\right)C_x=\left[\frac{1}{2}{\left(3\text{in}\text{.}\times \frac{1\text{ft}}{12\text{in}\text{.}}\right)}^2\left(0\right)+0.33333\left(\text{5}\text{in}\text{.}\times \frac{1\text{ft}}{12\text{in}\text{.}}\right){\left(18\right)}^2\right]\left(0.186335\right)\\ 0.6667C_x=-\left(0+45\right)\left(0.186335\right)\\ C_x=-\frac{8.385}{0.6667}\\ C_x=-12.58\text{lb}\end{array}$

Find the component of dynamic reaction at D $\left(D_x\right)$ along x-axis using equate the k- vector coefficients using Equation (9).

$2b{D}_x=-\left(-\frac{1}{2}{r}^2{\dot{\omega }}_1+0.33333c{\omega }_2^2\right)m$

Substitute 4 in. for b, 3 in. for r, 5 in. for c, 18 rad/s for ${\omega }_2$, and $0.186335\text{lb}\cdot {\text{s}}^2\text{/ft}$ for m.

$\begin{array}{l}2\left(4\text{in}\text{.}\times \frac{1\text{ft}}{12\text{in}\text{.}}\right)D_x=-\left[-\frac{1}{2}{\left(3\text{in}\text{.}\times \frac{1\text{ft}}{12\text{in}\text{.}}\right)}^2\left(0\right)+0.33333\left(\text{5}\text{in}\text{.}\times \frac{1\text{ft}}{12\text{in}\text{.}}\right){\left(18\right)}^2\right]\left(0.186335\right)\\ 0.6667D_x=-\left(0+45\right)\left(0.186335\right)\\ D_x=-\frac{8.385}{0.6667}\\ D_x=-12.58\text{lb}\end{array}$

Find the component of dynamic reaction at C $\left(C_z\right)$ along z-axis using equate the i- vector coefficients in Equation (8).

$2b{C}_z=\left(\frac{1}{2}{r}^2{\omega }_1{\omega }_2-0.33333c{\dot{\omega }}_2\right)m$ (10)

Substitute 4 in. for b, 3 in. for r, 60 rad/s for ${\omega }_1$, 18 rad/s for ${\omega }_2$, 5 in. for c, 0 for ${\dot{\omega }}_2$, and $0.186335\text{lb}\cdot {\text{s}}^2\text{/ft}$ for m.

$\begin{array}{l}2b{C}_z=\left(\frac{1}{2}{r}^2{\omega }_1{\omega }_2-0.33333c{\dot{\omega }}_2\right)m\\ 2\left(4\text{in}\text{.}\times \frac{1\text{ft}}{12\text{in}\text{.}}\right)C_z=\left[\frac{1}{2}{\left(3\text{in}\text{.}\times \frac{1\text{ft}}{12\text{in}\text{.}}\right)}^2\left(60\right)\left(18\right)+0.33333\left(\text{5}\text{in}\text{.}\times \frac{1\text{ft}}{12\text{in}\text{.}}\right)\left(0\right)\right]\left(0.186335\right)\\ 0.6667C_z=\left(33.75+0\right)\left(0.186335\right)\\ C_z=\frac{6.2888}{0.6667}\\ C_z=9.43\text{lb}\end{array}$

Find the component of dynamic reaction at D $\left(D_z\right)$ along z-axis using equate the i- vector coefficients in Equation (10).

$2b{C}_z=\left(-\frac{1}{2}{r}^2{\omega }_1{\omega }_2+0.33333c{\dot{\omega }}_2\right)m$ (10)

Substitute 4 in. for b, 3 in. for r, 60 rad/s for ${\omega }_1$, 18 rad/s for ${\omega }_2$, 5 in. for c, 0 for ${\dot{\omega }}_2$, and $0.186335\text{lb}\cdot {\text{s}}^2\text{/ft}$ for m.

$\begin{array}{l}2b{D}_z=\left(-\frac{1}{2}{r}^2{\omega }_1{\omega }_2+0.33333c{\dot{\omega }}_2\right)m\\ 2\left(4\text{in}\text{.}\times \frac{1\text{ft}}{12\text{in}\text{.}}\right)D_z=\left[\begin{array}{l}-\frac{1}{2}{\left(3\text{in}\text{.}\times \frac{1\text{ft}}{12\text{in}\text{.}}\right)}^2\left(60\right)\left(18\right)\\ -0.33333\left(\text{5}\text{in}\text{.}\times \frac{1\text{ft}}{12\text{in}\text{.}}\right)\left(0\right)\end{array}\right]\left(0.186335\right)\\ 0.6667D_z=\left(-33.75+0\right)\left(0.186335\right)\\ D_z=\frac{-6.2888}{0.6667}\\ D_z=-9.43\text{lb}\end{array}$

Find the dynamic reactions at C using the equation:

$C=C_{x}i+C_{z}k$

Substitute $-12.58\text{lb}$ for $C_x$ and 9.43 lb for $C_z$.

$C=-\left(12.58\text{lb}\right)i+\left(9.43\text{lb}\right)k$

Thus, the dynamic reactions at C after the couple has been removed is $\underset{\_}{-\left(12.58\text{lb}\right)i+\left(9.43\text{lb}\right)k}$.

Find the dynamic reactions at D using the equation:

$D=D_{x}i+D_{z}k$

Substitute $-12.58\text{lb}$ for $D_x$ and $-9.43\text{lb}$ for $D_z$.

$C=-\left(12.58\text{lb}\right)i-\left(9.43\text{lb}\right)k$

Thus, the dynamic reactions at D after the couple has been removed is $\underset{\_}{-\left(12.58\text{lb}\right)i-\left(9.43\text{lb}\right)k}$.