
Concept explainers
The dynamic reaction at C and D after the couple has been removed.
Answer to Problem 18.101P
The dynamic reaction at C after the couple has been removed is
The dynamic reaction at D after the couple has been removed is
Explanation of Solution
Given information:
The weight (W) of the disk is 6 lb.
The radius (r) of the disk is 3 in..
The angular velocity
The angular velocity of shaft CBD and arm AB is
The horizontal distance (c) between the center of rod CBD and center of disk is 5 in..
The vertical distance (b) between the center of rod CBD and center of disk is 4 in..
The couple
The time (t) of couple applied is 2 s.
Calculation:
Find the mass (m) of the disk using the equation:
Here, g is the acceleration due to gravity.
Substitute 6 lb for W and
Write the equation of vector form of angular velocity
The angular velocity
Write the equation of angular velocity of disk A
Write the equation of angular velocity
Find the equation of angular velocity
Substitute 0 for
Find the equation of angular momentum about A
Substitute 0 for
Find the rate of change of angular momentum
Here,
Write the equation of the rate of change of angular momentum about A
Substitute
Write the equation mass moment of inertia
Write the equation mass moment of inertia
Write the equation of velocity of the mass center A of the disk.
Write the equation of acceleration of the mass center A of the disk.
Substitute
Find the position vector of D with respect to A.
Substitute 5 in. for c and 4 in. for b.
Find the rate of change of angular momentum about D
Substitute
Substitute
Sketch the free body diagram and kinetic diagram of the system as shown in Figure (1).
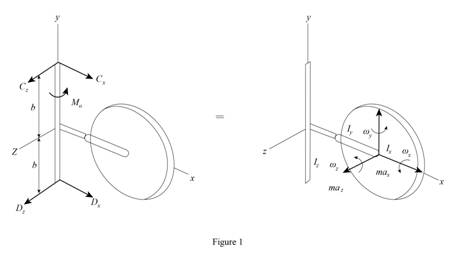
Refer Figure (1).
Apply Newton’s law of motion.
Substitute
Equate i-vector coefficients in Equation (3).
Equate k-vector coefficients in Equation (3).
Take moment about D.
Here,
The moment at D is equal to the rate of change of angular momentum at D.
Equate Equation (3) and (7).
Find the acceleration of shaft CBD and arm using equate the j- vector coefficients in Equation (8).
Substitute
After the 2 s, the couple
Find the angular velocity
Substitute 0 for
Find the component of dynamic reaction at C
Substitute 4 in. for b, 3 in. for r, 5 in. for c, and
Find the component of dynamic reaction at D
Substitute 4 in. for b, 3 in. for r, 5 in. for c, 14.18 rad/s for
Find the component of dynamic reaction at C
Substitute 4 in. for b, 3 in. for r, 60 rad/s for
Find the component of dynamic reaction at D
Substitute 4 in. for b, 3 in. for r, 60 rad/s for
Find the dynamic reactions at C using the equation:
Substitute
Thus, the dynamic reactions at C after the couple has been removed is
Find the dynamic reactions at D using the equation:
Substitute
Thus, the dynamic reactions at D after the couple has been removed is
Want to see more full solutions like this?
Chapter 18 Solutions
Vector Mechanics for Engineers: Statics and Dynamics
- Steam at 100 psia and 650°F is expanded adiabatically in a closed system to 10 psia. Determine the work produced, in Btu/lbm, and the final temperature of steam for an isentropic expansion efficiency of 80 percent. Use steam tables. The work produced is Btu/lbm. The final temperature of steam is °F.arrow_forwardComplet the solution : Vavg Ti Te Ts Q hexp Nuexp htheo Re Nutheo Error (m/s) (*C) (*C) (*C) (W) 2.11 18.8 21.3 45.8 2.61 18.5 20.8 46.3arrow_forwardA 48-kg iron block and a 76-kg copper block, both initially at 80°C, are dropped into a large lake at 15°C. Thermal equilibrium is established after a while as a result of heat transfer between the blocks and the lake water. Determine the total entropy change for this process. The specific heat of iron at room temperature is cp = 0.45 kJ/kg·K. The specific heat of copper at 27°C is cp = 0.386 kJ/kg·K. The total entropy change for this process is kJ/K.arrow_forward
- Please help Air at 4.4 MPa and 500°C is expanded in an adiabatic gas turbine to 0.2 MPa. Calculate the maximum work that this turbine can produce in kJ/kg. Use the table containing the ideal gas specific heats of various common gases. The maximum work that this turbine can produce is kJ/kg.arrow_forwardSaturated water vapor at 150°C is compressed in a reversible steady-flow device to 1150 kPa while its specific volume remains constant. Determine the work required in kJ/kg. Use steam tables. The work required is kJ/kg.arrow_forwardThree lbm of R-134a is expanded isentropically in a closed system from 100 psia and 100°F to 10 psia. Determine the total heat transfer and the work production for this process. Use the tables for R-134a. The total heat transfer is Btu. The work production for this process is Btu. Three lbm of R-134a is expanded isentropically in a closed system from 100 psia and 100°F to 10 psia. Determine the total heat transfer and the work production for this process. Use the tables for R-134a. The total heat transfer is Btu. The work production for this process is Btu.arrow_forward
- Oxygen at 300 kPa and 90°C flowing at an average velocity of 3 m/s is expanded in an adiabatic nozzle. What is the maximum velocity of the oxygen at the outlet of this nozzle when the outlet pressure is 60 kPa? Use the table containing the ideal gas specific heats of various common gases. The maximum velocity of the oxygen at the outlet of this nozzle is m/s.arrow_forwardThe well-insulated container shown in the given figure is initially evacuated. The supply line contains air that is maintained at 150 psia and 110°F. The valve is opened until the pressure in the container is the same as the pressure in the supply line. Determine the minimum temperature in the container when the valve is closed. Use the table containing the ideal gas specific heats of various common gases. A valve is shown at the vertical tube. The minimum temperature in the container when the valve is closed is °F.arrow_forwardDuring the isothermal heat addition process of a Carnot cycle, 1050 kJ of heat is added to the working fluid from a source at 400°C. NOTE: This is a multi-part question. Once an answer is submitted, you will be unable to return to this part. Determine the total entropy change for the process. The total entropy change for the process is kJ/K.arrow_forward
- Question 6 What kind of problem would arise if components of the strain tensor were defined as varrow_forwardplease show steps, thanksarrow_forwardYou design a pin joint. The pin is made of a material with the yield strength of 325 MPa and ultimate strength of 500 MPa. The maximum allowed stress in service is expressed as a tensor 0 100 0 σ 100 0 0 MPa 0 0 Evaluate the safety factor SF for stress in this design. Write answer unitless rounding to 2 decimal places and enter decimals even if those are zeros.arrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





