Introductory Algebra for College Students (7th Edition)
Introductory Algebra for College Students (7th Edition)
7th Edition
ISBN: 9780134178059
Author: Robert F. Blitzer
Publisher: PEARSON
bartleby

Concept explainers

Equations and Inequations
Equations and inequalities describe the relationship between two mathematical expressions.
Linear Functions
A linear function can just be a constant, or it can be the constant multiplied with the variable like x or y. If the variables are of the form, x2, x1/2 or y2 it is not linear. The exponent over the variables should always be 1.
bartleby

Videos

Textbook Question
Book Icon
Chapter 1.8, Problem 99ES

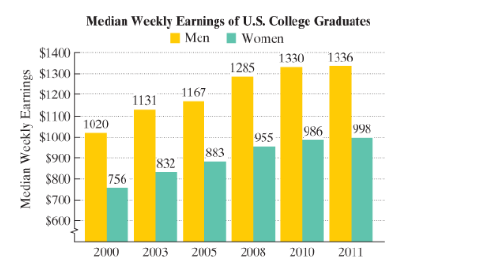
Chapter 1.8, Problem 99ES, The data can be described by the following mathematical models: M=2n2+170n+51155F=3n2+145n+37755 , example 1

Chapter 1.8, Problem 99ES, The data can be described by the following mathematical models: M=2n2+170n+51155F=3n2+145n+37755 , example 2

The data can be described by the following mathematical models:

   M = − 2 n 2 + 170 n + 5115 5 F = − 3 n 2 + 145 n + 3775 5

Median weekly earnings of male college graduates = M

Median weekly earning of female college graduates = F

In each mathematical model, n represents the number of years after 2000. Use this information to solve Exercises 99−100.

99.

a. Use the appropriate formula to find the median weekly earnings of male college graduates in 2010. Does this value underestimate or overestimate the earnings shown by the bar graph? By how much?

b. Use the appropriate formula to find the median weekly earnings of female college graduates in 2010 Does this value underestimate or overestimate the earnings shown by the bar graph? By how much?

c. Use the values given by the mathematical models in parts (a) and (b) to find the difference between men’s weekly earnings and women’s weekly earnings in 2010. How does this compare with the difference in earnings shown by the graph?

Expert Solution & Answer
Check Mark

Want to see the full answer?

Check out a sample textbook solution
Blurred answer
Previous
Chapter 1.8, Problem 98ES
Next
Chapter 1.8, Problem 100ES
Students have asked these similar questions
Question 6 Not yet answered Marked out of 5.00 Flag question = If (4,6,-11) and (-12,-16,4), = Compute the cross product vx w k
Consider the following vector field v^-> (x,y): v^->(x,y)=2yi−xj What is the magnitude of the vector v⃗  located in point (13,9)? [Provide your answer as an integer number (no fraction). For a decimal number, round your answer to 2 decimal places]
Question 4 Find the value of the first element for the first row of the inverse matrix of matrix B. 3 Not yet answered B = Marked out of 5.00 · (³ ;) Flag question 7 [Provide your answer as an integer number (no fraction). For a decimal number, round your answer to 2 decimal places] Answer:

Chapter 1 Solutions

Introductory Algebra for College Students (7th Edition)

Ch. 1.1 - Fill in each blank so that the resulting statement...Ch. 1.1 - Fill in each blank so that the resulting statement...Ch. 1.1 - Fill in each blank so that the resulting statement...Ch. 1.1 - Fill in each blank so that the resulting statement...Ch. 1.1 - Fill in each blank so that the resulting statement...Ch. 1.1 - In Exercises 114, evaluate each expression for x=4...Ch. 1.1 - In Exercises 114, evaluate each expression for x=4...Ch. 1.1 - In Exercises 114, evaluate each expression for x=4...Ch. 1.1 - In Exercises 114, evaluate each expression for x=4...Ch. 1.1 - In Exercises 114, evaluate each expression for x=4...
Ch. 1.1 - In Exercises 114, evaluate each expression for x=4...Ch. 1.1 - In Exercises 114, evaluate each expression for x=4...Ch. 1.1 - In Exercises 114, evaluate each expression for x=4...Ch. 1.1 - In Exercises 114, evaluate each expression for x=4...Ch. 1.1 - Prob. 10ESCh. 1.1 - Prob. 11ESCh. 1.1 - Prob. 12ESCh. 1.1 - Prob. 13ESCh. 1.1 - In Exercises 114, evaluate each expression for x=4...Ch. 1.1 - In Exercises 1524, evaluate each expression for...Ch. 1.1 - In Exercises 1524, evaluate each expression for...Ch. 1.1 - Prob. 17ESCh. 1.1 - Prob. 18ESCh. 1.1 - Prob. 19ESCh. 1.1 - Prob. 20ESCh. 1.1 - Prob. 21ESCh. 1.1 - In Exercises 1524, evaluate each expression for...Ch. 1.1 - Prob. 23ESCh. 1.1 - Prob. 24ESCh. 1.1 - In Exercises 2542, write each English phrase as an...Ch. 1.1 - In Exercises 2542, write each English phrase as an...Ch. 1.1 - In Exercises 2542, write each English phrase as an...Ch. 1.1 - Prob. 28ESCh. 1.1 - Prob. 29ESCh. 1.1 - Prob. 30ESCh. 1.1 - Prob. 31ESCh. 1.1 - Prob. 32ESCh. 1.1 - Prob. 33ESCh. 1.1 - Prob. 34ESCh. 1.1 - In Exercises 2542, write each English phrase as an...Ch. 1.1 - In Exercises 2542, write each English phrase as an...Ch. 1.1 - In Exercises 2542, write each English phrase as an...Ch. 1.1 - In Exercises 2542, write each English phrase as an...Ch. 1.1 - Prob. 39ESCh. 1.1 - Prob. 40ESCh. 1.1 - Prob. 41ESCh. 1.1 - Prob. 42ESCh. 1.1 - Prob. 43ESCh. 1.1 - Prob. 44ESCh. 1.1 - Prob. 45ESCh. 1.1 - In Exercises 4358, determine whether the given...Ch. 1.1 - In Exercises 4358, determine whether the given...Ch. 1.1 - In Exercises 4358, determine whether the given...Ch. 1.1 - Prob. 49ESCh. 1.1 - Prob. 50ESCh. 1.1 - Prob. 51ESCh. 1.1 - Prob. 52ESCh. 1.1 - Prob. 53ESCh. 1.1 - Prob. 54ESCh. 1.1 - Prob. 55ESCh. 1.1 - Prob. 56ESCh. 1.1 - Prob. 57ESCh. 1.1 - Prob. 58ESCh. 1.1 - Prob. 59ESCh. 1.1 - Prob. 60ESCh. 1.1 - In Exercises 5974, write each sentence as an...Ch. 1.1 - Prob. 62ESCh. 1.1 - Prob. 63ESCh. 1.1 - Prob. 64ESCh. 1.1 - Prob. 65ESCh. 1.1 - Prob. 66ESCh. 1.1 - Prob. 67ESCh. 1.1 - Prob. 68ESCh. 1.1 - Prob. 69ESCh. 1.1 - Prob. 70ESCh. 1.1 - Prob. 71ESCh. 1.1 - Prob. 72ESCh. 1.1 - Prob. 73ESCh. 1.1 - Prob. 74ESCh. 1.1 - Prob. 75ESCh. 1.1 - Prob. 76ESCh. 1.1 - Prob. 77ESCh. 1.1 - Prob. 78ESCh. 1.1 - Prob. 79ESCh. 1.1 - Prob. 80ESCh. 1.1 - Prob. 81ESCh. 1.1 - a. Evaluate 5x14 for x=3 and y=12 . b. Is the...Ch. 1.1 - Prob. 83ESCh. 1.1 - Prob. 84ESCh. 1.1 - Prob. 85ESCh. 1.1 - Prob. 86ESCh. 1.1 - Prob. 87ESCh. 1.1 - Prob. 88ESCh. 1.1 - Prob. 89ESCh. 1.1 - Prob. 90ESCh. 1.1 - Prob. 91ESCh. 1.1 - Prob. 92ESCh. 1.1 - Prob. 93ESCh. 1.1 - Prob. 94ESCh. 1.1 - Prob. 95ESCh. 1.1 - What is a mathematical model?Ch. 1.1 - Prob. 97ESCh. 1.1 - Prob. 98ESCh. 1.1 - Prob. 99ESCh. 1.1 - Prob. 100ESCh. 1.1 - Prob. 101ESCh. 1.1 - Prob. 102ESCh. 1.1 - Prob. 103ESCh. 1.1 - In Exercises 103106, determine whether each...Ch. 1.1 - Prob. 105ESCh. 1.1 - Prob. 106ESCh. 1.1 - In Exercises 107108, define variables and write a...Ch. 1.1 - In Exercises 107108, define variables and write a...Ch. 1.1 - Prob. 109ESCh. 1.1 - Prob. 110ESCh. 1.1 - Exercises 109111 will help you prepare for the...Ch. 1.2 - Fill in each blank so that the resulting statement...Ch. 1.2 - Fill in each blank so that the resulting statement...Ch. 1.2 - Prob. 3CAVCCh. 1.2 - Fill in each blank so that the resulting statement...Ch. 1.2 - Fill in each blank so that the resulting statement...Ch. 1.2 - Fill in each blank so that the resulting statement...Ch. 1.2 - Prob. 7CAVCCh. 1.2 - Prob. 8CAVCCh. 1.2 - Prob. 9CAVCCh. 1.2 - Prob. 10CAVCCh. 1.2 - Prob. 11CAVCCh. 1.2 - Prob. 12CAVCCh. 1.2 - Prob. 1ESCh. 1.2 - Prob. 2ESCh. 1.2 - In Exercises 16, convert each mixed number to an...Ch. 1.2 - In Exercises 16, convert each mixed number to an...Ch. 1.2 - In Exercises 16, convert each mixed number to an...Ch. 1.2 - Prob. 6ESCh. 1.2 - Prob. 7ESCh. 1.2 - Prob. 8ESCh. 1.2 - Prob. 9ESCh. 1.2 - Prob. 10ESCh. 1.2 - Prob. 11ESCh. 1.2 - Prob. 12ESCh. 1.2 - Prob. 13ESCh. 1.2 - In Exercises 1328, identify each natural number as...Ch. 1.2 - In Exercises 1328, identify each natural number as...Ch. 1.2 - In Exercises 1328, identify each natural number as...Ch. 1.2 - Prob. 17ESCh. 1.2 - Prob. 18ESCh. 1.2 - Prob. 19ESCh. 1.2 - Prob. 20ESCh. 1.2 - Prob. 21ESCh. 1.2 - Prob. 22ESCh. 1.2 - Prob. 23ESCh. 1.2 - Prob. 24ESCh. 1.2 - Prob. 25ESCh. 1.2 - Prob. 26ESCh. 1.2 - In Exercises 1328, identify each natural number as...Ch. 1.2 - In Exercises 1328, identify each natural number as...Ch. 1.2 - In Exercises 2940, simplify each fraction by...Ch. 1.2 - Prob. 30ESCh. 1.2 - Prob. 31ESCh. 1.2 - Prob. 32ESCh. 1.2 - Prob. 33ESCh. 1.2 - Prob. 34ESCh. 1.2 - Prob. 35ESCh. 1.2 - Prob. 36ESCh. 1.2 - In Exercises 2940, simplify each fraction by...Ch. 1.2 - In Exercises 2940, simplify each fraction by...Ch. 1.2 - In Exercises 2940, simplify each fraction by...Ch. 1.2 - Prob. 40ESCh. 1.2 - Prob. 41ESCh. 1.2 - Prob. 42ESCh. 1.2 - Prob. 43ESCh. 1.2 - Prob. 44ESCh. 1.2 - Prob. 45ESCh. 1.2 - Prob. 46ESCh. 1.2 - In Exercises 4190, perform the indicated...Ch. 1.2 - In Exercises 4190, perform the indicated...Ch. 1.2 - In Exercises 4190, perform the indicated...Ch. 1.2 - Prob. 50ESCh. 1.2 - Prob. 51ESCh. 1.2 - Prob. 52ESCh. 1.2 - Prob. 53ESCh. 1.2 - In Exercises 4190, perform the indicated...Ch. 1.2 - In Exercises 4190, perform the indicated...Ch. 1.2 - In Exercises 4190, perform the indicated...Ch. 1.2 - Prob. 57ESCh. 1.2 - Prob. 58ESCh. 1.2 - Prob. 59ESCh. 1.2 - Prob. 60ESCh. 1.2 - Prob. 61ESCh. 1.2 - In Exercises 4190, perform the indicated...Ch. 1.2 - In Exercises 4190, perform the indicated...Ch. 1.2 - Prob. 64ESCh. 1.2 - Prob. 65ESCh. 1.2 - Prob. 66ESCh. 1.2 - Prob. 67ESCh. 1.2 - In Exercises 4190, perform the indicated...Ch. 1.2 - In Exercises 4190, perform the indicated...Ch. 1.2 - In Exercises 4190, perform the indicated...Ch. 1.2 - In Exercises 4190, perform the indicated...Ch. 1.2 - Prob. 72ESCh. 1.2 - Prob. 73ESCh. 1.2 - Prob. 74ESCh. 1.2 - Prob. 75ESCh. 1.2 - Prob. 76ESCh. 1.2 - In Exercises 4190, perform the indicated...Ch. 1.2 - In Exercises 4190, perform the indicated...Ch. 1.2 - In Exercises 4190, perform the indicated...Ch. 1.2 - Prob. 80ESCh. 1.2 - Prob. 81ESCh. 1.2 - Prob. 82ESCh. 1.2 - Prob. 83ESCh. 1.2 - Prob. 84ESCh. 1.2 - Prob. 85ESCh. 1.2 - Prob. 86ESCh. 1.2 - In Exercises 4190, perform the indicated...Ch. 1.2 - In Exercises 4190, perform the indicated...Ch. 1.2 - In Exercises 4190, perform the indicated...Ch. 1.2 - Prob. 90ESCh. 1.2 - Prob. 91ESCh. 1.2 - Prob. 92ESCh. 1.2 - Prob. 93ESCh. 1.2 - Prob. 94ESCh. 1.2 - Prob. 95ESCh. 1.2 - Prob. 96ESCh. 1.2 - In Exercises 91102, determine whether the given...Ch. 1.2 - In Exercises 91102, determine whether the given...Ch. 1.2 - In Exercises 91102, determine whether the given...Ch. 1.2 - Prob. 100ESCh. 1.2 - Prob. 101ESCh. 1.2 - Prob. 102ESCh. 1.2 - Prob. 103ESCh. 1.2 - Prob. 104ESCh. 1.2 - Prob. 105ESCh. 1.2 - In Exercises 103114, translate from English to an...Ch. 1.2 - In Exercises 103114, translate from English to an...Ch. 1.2 - In Exercises 103114, translate from English to an...Ch. 1.2 - Prob. 109ESCh. 1.2 - Prob. 110ESCh. 1.2 - Prob. 111ESCh. 1.2 - Prob. 112ESCh. 1.2 - Prob. 113ESCh. 1.2 - Prob. 114ESCh. 1.2 - Prob. 115ESCh. 1.2 - Prob. 116ESCh. 1.2 - In Exercises 11518, perform the indicated...Ch. 1.2 - In Exercises 11518, perform the indicated...Ch. 1.2 - Prob. 119ESCh. 1.2 - Prob. 120ESCh. 1.2 - Prob. 121ESCh. 1.2 - Prob. 122ESCh. 1.2 - Prob. 123ESCh. 1.2 - Prob. 124ESCh. 1.2 - Prob. 125ESCh. 1.2 - Prob. 126ESCh. 1.2 - Prob. 127ESCh. 1.2 - Prob. 128ESCh. 1.2 - The bar graph shows that the fraction of U.S...Ch. 1.2 - The bar graph shows that the fraction of U.S...Ch. 1.2 - Prob. 131ESCh. 1.2 - Prob. 132ESCh. 1.2 - Prob. 133ESCh. 1.2 - Prob. 134ESCh. 1.2 - Prob. 135ESCh. 1.2 - Prob. 136ESCh. 1.2 - Prob. 137ESCh. 1.2 - Prob. 138ESCh. 1.2 - Prob. 139ESCh. 1.2 - Prob. 140ESCh. 1.2 - Prob. 141ESCh. 1.2 - Make Sense? In Exercises 141144, determine whether...Ch. 1.2 - Prob. 143ESCh. 1.2 - Prob. 144ESCh. 1.2 - In Exercises 145148, determine whether each...Ch. 1.2 - Prob. 146ESCh. 1.2 - Prob. 147ESCh. 1.2 - Prob. 148ESCh. 1.2 - Prob. 149ESCh. 1.2 - Prob. 150ESCh. 1.2 - Prob. 151ESCh. 1.2 - Prob. 152ESCh. 1.3 - Fill in each blank so that the resulting statement...Ch. 1.3 - Fill in each blank so that the resulting statement...Ch. 1.3 - Prob. 3CAVCCh. 1.3 - Prob. 4CAVCCh. 1.3 - Prob. 5CAVCCh. 1.3 - Prob. 6CAVCCh. 1.3 - Prob. 7CAVCCh. 1.3 - Prob. 8CAVCCh. 1.3 - Prob. 1ESCh. 1.3 - Prob. 2ESCh. 1.3 - Prob. 3ESCh. 1.3 - Prob. 4ESCh. 1.3 - In Exercises 18, write a positive or negative...Ch. 1.3 - Prob. 6ESCh. 1.3 - Prob. 7ESCh. 1.3 - Prob. 8ESCh. 1.3 - Prob. 9ESCh. 1.3 - Prob. 10ESCh. 1.3 - Prob. 11ESCh. 1.3 - Prob. 12ESCh. 1.3 - Prob. 13ESCh. 1.3 - Prob. 14ESCh. 1.3 - Prob. 15ESCh. 1.3 - Prob. 16ESCh. 1.3 - Prob. 17ESCh. 1.3 - Prob. 18ESCh. 1.3 - Prob. 19ESCh. 1.3 - Prob. 20ESCh. 1.3 - Prob. 21ESCh. 1.3 - Prob. 22ESCh. 1.3 - Prob. 23ESCh. 1.3 - Prob. 24ESCh. 1.3 - Prob. 25ESCh. 1.3 - Prob. 26ESCh. 1.3 - Prob. 27ESCh. 1.3 - Prob. 28ESCh. 1.3 - Prob. 29ESCh. 1.3 - Prob. 30ESCh. 1.3 - Prob. 31ESCh. 1.3 - Prob. 32ESCh. 1.3 - Prob. 33ESCh. 1.3 - In Exercises 3336, list all numbers from the given...Ch. 1.3 - In Exercises 3336, list all numbers from the given...Ch. 1.3 - In Exercises 3336, list all numbers from the given...Ch. 1.3 - Prob. 37ESCh. 1.3 - Prob. 38ESCh. 1.3 - Prob. 39ESCh. 1.3 - Prob. 40ESCh. 1.3 - Prob. 41ESCh. 1.3 - Prob. 42ESCh. 1.3 - Prob. 43ESCh. 1.3 - an example of a number that is a real number, but...Ch. 1.3 - In Exercises 4562, insert either < or > in the...Ch. 1.3 - In Exercises 4562, insert either < or > in the...Ch. 1.3 - Prob. 47ESCh. 1.3 - Prob. 48ESCh. 1.3 - Prob. 49ESCh. 1.3 - Prob. 50ESCh. 1.3 - Prob. 51ESCh. 1.3 - Prob. 52ESCh. 1.3 - In Exercises 4562, insert either < or > in the...Ch. 1.3 - In Exercises 4562, insert either < or > in the...Ch. 1.3 - In Exercises 4562, insert either < or > in the...Ch. 1.3 - Prob. 56ESCh. 1.3 - Prob. 57ESCh. 1.3 - Prob. 58ESCh. 1.3 - Prob. 59ESCh. 1.3 - In Exercises 4562, insert either < or > in the...Ch. 1.3 - In Exercises 4562, insert either < or > in the...Ch. 1.3 - Prob. 62ESCh. 1.3 - Prob. 63ESCh. 1.3 - In Exercises 6370, determine whether each...Ch. 1.3 - Prob. 65ESCh. 1.3 - Prob. 66ESCh. 1.3 - In Exercises 6370, determine whether each...Ch. 1.3 - In Exercises 6370, determine whether each...Ch. 1.3 - In Exercises 6370, determine whether each...Ch. 1.3 - Prob. 70ESCh. 1.3 - Prob. 71ESCh. 1.3 - Prob. 72ESCh. 1.3 - Prob. 73ESCh. 1.3 - Prob. 74ESCh. 1.3 - Prob. 75ESCh. 1.3 - Prob. 76ESCh. 1.3 - In Exercises 7178, find each absolute value. 77....Ch. 1.3 - In Exercises 7178, find each absolute value. 78....Ch. 1.3 - In Exercises 7986, insert either <, >, or = in the...Ch. 1.3 - Prob. 80ESCh. 1.3 - Prob. 81ESCh. 1.3 - Prob. 82ESCh. 1.3 - Prob. 83ESCh. 1.3 - Prob. 84ESCh. 1.3 - Prob. 85ESCh. 1.3 - Prob. 86ESCh. 1.3 - Prob. 87ESCh. 1.3 - In, Exercises 8794, determine whether natural...Ch. 1.3 - In, Exercises 8794, determine whether natural...Ch. 1.3 - In, Exercises 8794, determine whether natural...Ch. 1.3 - Prob. 91ESCh. 1.3 - Prob. 92ESCh. 1.3 - Prob. 93ESCh. 1.3 - Prob. 94ESCh. 1.3 - Prob. 95ESCh. 1.3 - Prob. 96ESCh. 1.3 - Prob. 97ESCh. 1.3 - What are the natural numbers?Ch. 1.3 - What are the whole numbers?Ch. 1.3 - What are the integers?Ch. 1.3 - Prob. 101ESCh. 1.3 - Prob. 102ESCh. 1.3 - Prob. 103ESCh. 1.3 - Prob. 104ESCh. 1.3 - Prob. 105ESCh. 1.3 - Prob. 106ESCh. 1.3 - Prob. 107ESCh. 1.3 - Make Sense? In Exercises 108111, determine whether...Ch. 1.3 - Make Sense? In Exercises 108111, determine whether...Ch. 1.3 - Make Sense? In Exercises 108111, determine whether...Ch. 1.3 - Prob. 111ESCh. 1.3 - Prob. 112ESCh. 1.3 - Prob. 113ESCh. 1.3 - Prob. 114ESCh. 1.3 - Prob. 115ESCh. 1.3 - Prob. 116ESCh. 1.3 - Prob. 117ESCh. 1.3 - In Exercises 118119, write each phrase as an...Ch. 1.3 - In Exercises 118119, write each phrase as an...Ch. 1.3 - In Exercises 120123, use a calculator to find a...Ch. 1.3 - In Exercises 120123, use a calculator to find a...Ch. 1.3 - In Exercises 120123, use a calculator to find a...Ch. 1.3 - Prob. 123ESCh. 1.3 - Prob. 124ESCh. 1.3 - Prob. 125ESCh. 1.3 - Prob. 126ESCh. 1.4 - Prob. 1CAVCCh. 1.4 - Prob. 2CAVCCh. 1.4 - Fill in each blank so that the resulting statement...Ch. 1.4 - Fill in each blank so that the resulting statement...Ch. 1.4 - Fill in each blank so that the resulting statement...Ch. 1.4 - Prob. 6CAVCCh. 1.4 - Prob. 7CAVCCh. 1.4 - Prob. 1ESCh. 1.4 - Prob. 2ESCh. 1.4 - Prob. 3ESCh. 1.4 - Prob. 4ESCh. 1.4 - Prob. 5ESCh. 1.4 - In Exercises 16, an algebraic expression is given....Ch. 1.4 - In Exercises 714, use the commutative property of...Ch. 1.4 - In Exercises 714, use the commutative property of...Ch. 1.4 - Prob. 9ESCh. 1.4 - In Exercises 714, use the commutative property of...Ch. 1.4 - Prob. 11ESCh. 1.4 - Prob. 12ESCh. 1.4 - Prob. 13ESCh. 1.4 - Prob. 14ESCh. 1.4 - Prob. 15ESCh. 1.4 - In Exercises 1522, use the commutative property of...Ch. 1.4 - In Exercises 1522, use the commutative property of...Ch. 1.4 - In Exercises 1522, use the commutative property of...Ch. 1.4 - Prob. 19ESCh. 1.4 - Prob. 20ESCh. 1.4 - Prob. 21ESCh. 1.4 - Prob. 22ESCh. 1.4 - Prob. 23ESCh. 1.4 - Prob. 24ESCh. 1.4 - Prob. 25ESCh. 1.4 - Prob. 26ESCh. 1.4 - Prob. 27ESCh. 1.4 - Prob. 28ESCh. 1.4 - Prob. 29ESCh. 1.4 - Prob. 30ESCh. 1.4 - Prob. 31ESCh. 1.4 - Prob. 32ESCh. 1.4 - Prob. 33ESCh. 1.4 - Prob. 34ESCh. 1.4 - Prob. 35ESCh. 1.4 - Prob. 36ESCh. 1.4 - Prob. 37ESCh. 1.4 - Prob. 38ESCh. 1.4 - In Exercises 2746, use a form of the distributive...Ch. 1.4 - Prob. 40ESCh. 1.4 - Prob. 41ESCh. 1.4 - Prob. 42ESCh. 1.4 - Prob. 43ESCh. 1.4 - Prob. 44ESCh. 1.4 - Prob. 45ESCh. 1.4 - Prob. 46ESCh. 1.4 - Prob. 47ESCh. 1.4 - Prob. 48ESCh. 1.4 - Prob. 49ESCh. 1.4 - Prob. 50ESCh. 1.4 - Prob. 51ESCh. 1.4 - Prob. 52ESCh. 1.4 - Prob. 53ESCh. 1.4 - Prob. 54ESCh. 1.4 - Prob. 55ESCh. 1.4 - Prob. 56ESCh. 1.4 - Prob. 57ESCh. 1.4 - Prob. 58ESCh. 1.4 - Prob. 59ESCh. 1.4 - Prob. 60ESCh. 1.4 - Prob. 61ESCh. 1.4 - Prob. 62ESCh. 1.4 - Prob. 63ESCh. 1.4 - Prob. 64ESCh. 1.4 - Prob. 65ESCh. 1.4 - Prob. 66ESCh. 1.4 - Prob. 67ESCh. 1.4 - Prob. 68ESCh. 1.4 - Prob. 69ESCh. 1.4 - Prob. 70ESCh. 1.4 - Prob. 71ESCh. 1.4 - Prob. 72ESCh. 1.4 - Prob. 73ESCh. 1.4 - Prob. 74ESCh. 1.4 - Prob. 75ESCh. 1.4 - Prob. 76ESCh. 1.4 - Prob. 77ESCh. 1.4 - Prob. 78ESCh. 1.4 - Prob. 79ESCh. 1.4 - Prob. 80ESCh. 1.4 - Prob. 81ESCh. 1.4 - Prob. 82ESCh. 1.4 - Prob. 83ESCh. 1.4 - Prob. 84ESCh. 1.4 - Prob. 85ESCh. 1.4 - Prob. 86ESCh. 1.4 - Art algebra student incorrectly used the...Ch. 1.4 - Prob. 88ESCh. 1.4 - Prob. 89ESCh. 1.4 - Prob. 90ESCh. 1.4 - Make Sense? In Exercises 8992, determine whether...Ch. 1.4 - Prob. 92ESCh. 1.4 - Prob. 93ESCh. 1.4 - Prob. 94ESCh. 1.4 - Prob. 95ESCh. 1.4 - Prob. 96ESCh. 1.4 - Prob. 97ESCh. 1.4 - Exercises 9799, will help you prepare for the...Ch. 1.4 - Exercises 9799, will help you prepare for the...Ch. 1.5 - Prob. 1CAVCCh. 1.5 - Prob. 2CAVCCh. 1.5 - In the remaining items, state whether each sum is...Ch. 1.5 - Prob. 4CAVCCh. 1.5 - Prob. 5CAVCCh. 1.5 - In the remaining items, state whether each sum is...Ch. 1.5 - Prob. 7CAVCCh. 1.5 - Prob. 8CAVCCh. 1.5 - In Exercises 18, find each sum using a number...Ch. 1.5 - In Exercises 18, find each sum using a number...Ch. 1.5 - In Exercises 18, find each sum using a number...Ch. 1.5 - Prob. 4ESCh. 1.5 - Prob. 5ESCh. 1.5 - Prob. 6ESCh. 1.5 - Prob. 7ESCh. 1.5 - Prob. 8ESCh. 1.5 - Prob. 9ESCh. 1.5 - Prob. 10ESCh. 1.5 - Prob. 11ESCh. 1.5 - In Exercises 946, find each sum without the use of...Ch. 1.5 - In Exercises 946, find each sum without the use of...Ch. 1.5 - In Exercises 946, find each sum without the use of...Ch. 1.5 - Prob. 15ESCh. 1.5 - Prob. 16ESCh. 1.5 - Prob. 17ESCh. 1.5 - Prob. 18ESCh. 1.5 - Prob. 19ESCh. 1.5 - In Exercises 946, find each sum without the use of...Ch. 1.5 - In Exercises 946, find each sum without the use of...Ch. 1.5 - In Exercises 946, find each sum without the use of...Ch. 1.5 - In Exercises 946, find each sum without the use of...Ch. 1.5 - In Exercises 946, find each sum without the use of...Ch. 1.5 - Prob. 25ESCh. 1.5 - Prob. 26ESCh. 1.5 - Prob. 27ESCh. 1.5 - Prob. 28ESCh. 1.5 - Prob. 29ESCh. 1.5 - Prob. 30ESCh. 1.5 - Prob. 31ESCh. 1.5 - Prob. 32ESCh. 1.5 - In Exercises 946, find each sum without the use of...Ch. 1.5 - In Exercises 946, find each sum without the use of...Ch. 1.5 - In Exercises 946, find each sum without the use of...Ch. 1.5 - Prob. 36ESCh. 1.5 - Prob. 37ESCh. 1.5 - Prob. 38ESCh. 1.5 - Prob. 39ESCh. 1.5 - Prob. 40ESCh. 1.5 - Prob. 41ESCh. 1.5 - Prob. 42ESCh. 1.5 - In Exercises 946, find each sum without the use of...Ch. 1.5 - In Exercises 946, find each sum without the use of...Ch. 1.5 - In Exercises 946, find each sum without the use of...Ch. 1.5 - Prob. 46ESCh. 1.5 - Prob. 47ESCh. 1.5 - Prob. 48ESCh. 1.5 - Prob. 49ESCh. 1.5 - Prob. 50ESCh. 1.5 - Prob. 51ESCh. 1.5 - Prob. 52ESCh. 1.5 - In Exercises 4760, simplify each algebraic...Ch. 1.5 - In Exercises 4760, simplify each algebraic...Ch. 1.5 - In Exercises 4760, simplify each algebraic...Ch. 1.5 - Prob. 56ESCh. 1.5 - Prob. 57ESCh. 1.5 - Prob. 58ESCh. 1.5 - In Exercises 4760, simplify each algebraic...Ch. 1.5 - Prob. 60ESCh. 1.5 - Prob. 61ESCh. 1.5 - Prob. 62ESCh. 1.5 - Prob. 63ESCh. 1.5 - In Exercises 6164, find each sum. 64....Ch. 1.5 - In Exercises 6566, insert, either <, >, or = in...Ch. 1.5 - In Exercises 6566, insert, either <, >, or = in...Ch. 1.5 - Prob. 67ESCh. 1.5 - Prob. 68ESCh. 1.5 - Prob. 69ESCh. 1.5 - Prob. 70ESCh. 1.5 - Prob. 71ESCh. 1.5 - Prob. 72ESCh. 1.5 - Solve Exercises 7178 by writing a sum of signed...Ch. 1.5 - Solve Exercises 7178 by writing a sum of signed...Ch. 1.5 - Solve Exercises 7178 by writing a sum of signed...Ch. 1.5 - Prob. 76ESCh. 1.5 - Solve Exercises 7178 by writing a sum of signed...Ch. 1.5 - Prob. 78ESCh. 1.5 - Prob. 79ESCh. 1.5 - The bar graph shows that in 2001, the U.S....Ch. 1.5 - Explain how to add two numbers with a number line....Ch. 1.5 - Prob. 82ESCh. 1.5 - Prob. 83ESCh. 1.5 - Prob. 84ESCh. 1.5 - Prob. 85ESCh. 1.5 - Prob. 86ESCh. 1.5 - Without a calculator, you can add numbers using a...Ch. 1.5 - Prob. 88ESCh. 1.5 - Prob. 89ESCh. 1.5 - Make Sense? In Exercises 8891, determine whether...Ch. 1.5 - Make Sense? In Exercises 8891, determine whether...Ch. 1.5 - In Exercises 9295, determine whether each...Ch. 1.5 - Prob. 93ESCh. 1.5 - In Exercises 9295, determine whether each...Ch. 1.5 - Prob. 95ESCh. 1.5 - Prob. 96ESCh. 1.5 - Prob. 97ESCh. 1.5 - Prob. 98ESCh. 1.5 - Prob. 99ESCh. 1.5 - Prob. 100ESCh. 1.5 - Use a calculator to verify any three of the...Ch. 1.5 - Consider the set {6,,0,0.7,3,4} . List all numbers...Ch. 1.5 - Determine whether this inequality is true or...Ch. 1.5 - Prob. 104ESCh. 1.5 - Prob. 105ESCh. 1.5 - Prob. 106ESCh. 1.5 - Prob. 107ESCh. 1.6 - Fill in each blank so that the resulting statement...Ch. 1.6 - Fill in each blank so that the resulting statement...Ch. 1.6 - Fill in each blank so that the resulting statement...Ch. 1.6 - Prob. 4CAVCCh. 1.6 - Prob. 5CAVCCh. 1.6 - Prob. 6CAVCCh. 1.6 - Prob. 7CAVCCh. 1.6 - Prob. 1ESCh. 1.6 - Consider the subtraction 410 . a Find the...Ch. 1.6 - Consider the subtraction 5(7) . a. Find the...Ch. 1.6 - Consider the subtraction 2(8) . a. Find the...Ch. 1.6 - Prob. 5ESCh. 1.6 - Prob. 6ESCh. 1.6 - In Exercises 550, perform the indicated...Ch. 1.6 - In Exercises 550, perform the indicated...Ch. 1.6 - Prob. 9ESCh. 1.6 - Prob. 10ESCh. 1.6 - Prob. 11ESCh. 1.6 - Prob. 12ESCh. 1.6 - Prob. 13ESCh. 1.6 - Prob. 14ESCh. 1.6 - Prob. 15ESCh. 1.6 - Prob. 16ESCh. 1.6 - Prob. 17ESCh. 1.6 - Prob. 18ESCh. 1.6 - Prob. 19ESCh. 1.6 - Prob. 20ESCh. 1.6 - In Exercises 550, perform the indicated...Ch. 1.6 - Prob. 22ESCh. 1.6 - Prob. 23ESCh. 1.6 - Prob. 24ESCh. 1.6 - Prob. 25ESCh. 1.6 - Prob. 26ESCh. 1.6 - Prob. 27ESCh. 1.6 - Prob. 28ESCh. 1.6 - Prob. 29ESCh. 1.6 - Prob. 30ESCh. 1.6 - Prob. 31ESCh. 1.6 - Prob. 32ESCh. 1.6 - Prob. 33ESCh. 1.6 - Prob. 34ESCh. 1.6 - Prob. 35ESCh. 1.6 - Prob. 36ESCh. 1.6 - Prob. 37ESCh. 1.6 - Prob. 38ESCh. 1.6 - Prob. 39ESCh. 1.6 - Prob. 40ESCh. 1.6 - Prob. 41ESCh. 1.6 - Prob. 42ESCh. 1.6 - Prob. 43ESCh. 1.6 - Prob. 44ESCh. 1.6 - Prob. 45ESCh. 1.6 - Prob. 46ESCh. 1.6 - Prob. 47ESCh. 1.6 - Prob. 48ESCh. 1.6 - Prob. 49ESCh. 1.6 - Prob. 50ESCh. 1.6 - Prob. 51ESCh. 1.6 - Prob. 52ESCh. 1.6 - Prob. 53ESCh. 1.6 - Prob. 54ESCh. 1.6 - Prob. 55ESCh. 1.6 - Prob. 56ESCh. 1.6 - Prob. 57ESCh. 1.6 - Prob. 58ESCh. 1.6 - Prob. 59ESCh. 1.6 - Prob. 60ESCh. 1.6 - Prob. 61ESCh. 1.6 - Prob. 62ESCh. 1.6 - Prob. 63ESCh. 1.6 - Prob. 64ESCh. 1.6 - Prob. 65ESCh. 1.6 - Prob. 66ESCh. 1.6 - Prob. 67ESCh. 1.6 - Prob. 68ESCh. 1.6 - Prob. 69ESCh. 1.6 - Prob. 70ESCh. 1.6 - Prob. 71ESCh. 1.6 - Prob. 72ESCh. 1.6 - Prob. 73ESCh. 1.6 - Prob. 74ESCh. 1.6 - Prob. 75ESCh. 1.6 - Prob. 76ESCh. 1.6 - In Exercises 7384, simplify each algebraic...Ch. 1.6 - In Exercises 7384, simplify each algebraic...Ch. 1.6 - Prob. 79ESCh. 1.6 - Prob. 80ESCh. 1.6 - Prob. 81ESCh. 1.6 - Prob. 82ESCh. 1.6 - Prob. 83ESCh. 1.6 - Prob. 84ESCh. 1.6 - In Exercises 8590, find the value of each...Ch. 1.6 - In Exercises 8590, find the value of each...Ch. 1.6 - In Exercises 8590, find the value of each...Ch. 1.6 - Prob. 88ESCh. 1.6 - Prob. 89ESCh. 1.6 - Prob. 90ESCh. 1.6 - Prob. 91ESCh. 1.6 - Prob. 92ESCh. 1.6 - Prob. 93ESCh. 1.6 - Prob. 94ESCh. 1.6 - Prob. 95ESCh. 1.6 - The peak of Mount Whitney is 14,494 feet above sea...Ch. 1.6 - In Exercises 97106, we return to the number line...Ch. 1.6 - In Exercises 97106, we return to the number line...Ch. 1.6 - In Exercises 97106, we return to the number line...Ch. 1.6 - Prob. 100ESCh. 1.6 - Prob. 101ESCh. 1.6 - Prob. 102ESCh. 1.6 - Prob. 103ESCh. 1.6 - Prob. 104ESCh. 1.6 - In Exercises 97106, we return to the number line...Ch. 1.6 - In Exercises 97106, we return to the number line...Ch. 1.6 - Prob. 107ESCh. 1.6 - Prob. 108ESCh. 1.6 - Prob. 109ESCh. 1.6 - Prob. 110ESCh. 1.6 - Explain how to subtract real numbers.Ch. 1.6 - How is 4(2) read?Ch. 1.6 - Explain how to simplify a series of additions and...Ch. 1.6 - Prob. 114ESCh. 1.6 - Prob. 115ESCh. 1.6 - Prob. 116ESCh. 1.6 - Prob. 117ESCh. 1.6 - Prob. 118ESCh. 1.6 - Make Sense? In Exercises 116119, determine whether...Ch. 1.6 - In Exercises 120123, determine whether each...Ch. 1.6 - In Exercises 120123, determine whether each...Ch. 1.6 - Prob. 122ESCh. 1.6 - Prob. 123ESCh. 1.6 - In Exercises 124127, use the number line to...Ch. 1.6 - In Exercises 124127, use the number line to...Ch. 1.6 - In Exercises 124127, use the number line to...Ch. 1.6 - In Exercises 124127, use the number line to...Ch. 1.6 - Prob. 128ESCh. 1.6 - Prob. 129ESCh. 1.6 - Prob. 130ESCh. 1.6 - Prob. 131ESCh. 1.6 - Prob. 132ESCh. 1.6 - Give an example of an integer that is not a...Ch. 1.6 - Exercises 134136 will help you prepare for the...Ch. 1.6 - Exercises 134136 will help you prepare for the...Ch. 1.6 - Prob. 136ESCh. 1.7 - Use the choices below to fill in each blank so...Ch. 1.7 - Prob. 2CAVCCh. 1.7 - Prob. 3CAVCCh. 1.7 - Prob. 4CAVCCh. 1.7 - Prob. 5CAVCCh. 1.7 - Prob. 6CAVCCh. 1.7 - Prob. 7CAVCCh. 1.7 - Use the choices below to fill in each blank so...Ch. 1.7 - Use the choices below to fill in each blank so...Ch. 1.7 - Use the choices below to fill in each blank so...Ch. 1.7 - Prob. 11CAVCCh. 1.7 - Prob. 1ESCh. 1.7 - Prob. 2ESCh. 1.7 - Prob. 3ESCh. 1.7 - Prob. 4ESCh. 1.7 - Prob. 5ESCh. 1.7 - Prob. 6ESCh. 1.7 - Prob. 7ESCh. 1.7 - In Exercises 134, perform the indicated...Ch. 1.7 - In Exercises 134, perform the indicated...Ch. 1.7 - In Exercises 134, perform the indicated...Ch. 1.7 - Prob. 11ESCh. 1.7 - Prob. 12ESCh. 1.7 - Prob. 13ESCh. 1.7 - Prob. 14ESCh. 1.7 - Prob. 15ESCh. 1.7 - Prob. 16ESCh. 1.7 - Prob. 17ESCh. 1.7 - In Exercises 134, perform the indicated...Ch. 1.7 - In Exercises 134, perform the indicated...Ch. 1.7 - In Exercises 134, perform the indicated...Ch. 1.7 - Prob. 21ESCh. 1.7 - Prob. 22ESCh. 1.7 - Prob. 23ESCh. 1.7 - Prob. 24ESCh. 1.7 - Prob. 25ESCh. 1.7 - Prob. 26ESCh. 1.7 - Prob. 27ESCh. 1.7 - In Exercises 134, perform the indicated...Ch. 1.7 - In Exercises 134, perform the indicated...Ch. 1.7 - In Exercises 134, perform the indicated...Ch. 1.7 - Prob. 31ESCh. 1.7 - Prob. 32ESCh. 1.7 - Prob. 33ESCh. 1.7 - Prob. 34ESCh. 1.7 - Prob. 35ESCh. 1.7 - Prob. 36ESCh. 1.7 - Prob. 37ESCh. 1.7 - In Exercises 3542, find the multiplicative in...Ch. 1.7 - In Exercises 3542, find the multiplicative in...Ch. 1.7 - In Exercises 3542, find the multiplicative in...Ch. 1.7 - Prob. 41ESCh. 1.7 - Prob. 42ESCh. 1.7 - Prob. 43ESCh. 1.7 - Prob. 44ESCh. 1.7 - Prob. 45ESCh. 1.7 - Prob. 46ESCh. 1.7 - In Exercises 4776, perform the indicated division...Ch. 1.7 - In Exercises 4776, perform the indicated division...Ch. 1.7 - In Exercises 4776, perform the indicated division...Ch. 1.7 - Prob. 50ESCh. 1.7 - Prob. 51ESCh. 1.7 - Prob. 52ESCh. 1.7 - Prob. 53ESCh. 1.7 - Prob. 54ESCh. 1.7 - Prob. 55ESCh. 1.7 - Prob. 56ESCh. 1.7 - Prob. 57ESCh. 1.7 - In Exercises 4776, perform the indicated division...Ch. 1.7 - Prob. 59ESCh. 1.7 - Prob. 60ESCh. 1.7 - Prob. 61ESCh. 1.7 - Prob. 62ESCh. 1.7 - Prob. 63ESCh. 1.7 - Prob. 64ESCh. 1.7 - Prob. 65ESCh. 1.7 - Prob. 66ESCh. 1.7 - Prob. 67ESCh. 1.7 - Prob. 68ESCh. 1.7 - Prob. 69ESCh. 1.7 - Prob. 70ESCh. 1.7 - Prob. 71ESCh. 1.7 - Prob. 72ESCh. 1.7 - Prob. 73ESCh. 1.7 - Prob. 74ESCh. 1.7 - Prob. 75ESCh. 1.7 - Prob. 76ESCh. 1.7 - Prob. 77ESCh. 1.7 - Prob. 78ESCh. 1.7 - Prob. 79ESCh. 1.7 - Prob. 80ESCh. 1.7 - Prob. 81ESCh. 1.7 - Prob. 82ESCh. 1.7 - Prob. 83ESCh. 1.7 - Prob. 84ESCh. 1.7 - Prob. 85ESCh. 1.7 - Prob. 86ESCh. 1.7 - Prob. 87ESCh. 1.7 - Prob. 88ESCh. 1.7 - Prob. 89ESCh. 1.7 - Prob. 90ESCh. 1.7 - Prob. 91ESCh. 1.7 - Prob. 92ESCh. 1.7 - Prob. 93ESCh. 1.7 - Prob. 94ESCh. 1.7 - Prob. 95ESCh. 1.7 - Prob. 96ESCh. 1.7 - Prob. 97ESCh. 1.7 - Prob. 98ESCh. 1.7 - Prob. 99ESCh. 1.7 - Prob. 100ESCh. 1.7 - Prob. 101ESCh. 1.7 - Prob. 102ESCh. 1.7 - Prob. 103ESCh. 1.7 - Prob. 104ESCh. 1.7 - Prob. 105ESCh. 1.7 - Prob. 106ESCh. 1.7 - Prob. 107ESCh. 1.7 - Prob. 108ESCh. 1.7 - Prob. 109ESCh. 1.7 - Prob. 110ESCh. 1.7 - Prob. 111ESCh. 1.7 - Prob. 112ESCh. 1.7 - Prob. 113ESCh. 1.7 - Prob. 114ESCh. 1.7 - Prob. 115ESCh. 1.7 - Prob. 116ESCh. 1.7 - Prob. 117ESCh. 1.7 - Prob. 118ESCh. 1.7 - C=0.5x+42 Percentage of American who smoked...Ch. 1.7 - C=0.5x+42 Percentage of American who smoked...Ch. 1.7 - Prob. 121ESCh. 1.7 - Prob. 122ESCh. 1.7 - Prob. 123ESCh. 1.7 - Prob. 124ESCh. 1.7 - Explain how to find the multiplicative inverse of...Ch. 1.7 - Prob. 126ESCh. 1.7 - Explain how to divide real numbers.Ch. 1.7 - Why is division by zero undefined?Ch. 1.7 - Prob. 129ESCh. 1.7 - Prob. 130ESCh. 1.7 - Prob. 131ESCh. 1.7 - Prob. 132ESCh. 1.7 - Prob. 133ESCh. 1.7 - Prob. 134ESCh. 1.7 - In Exercises 135138, determine whether each...Ch. 1.7 - In Exercises 135138, determine whether each...Ch. 1.7 - In Exercises 135138, determine whether each...Ch. 1.7 - Prob. 138ESCh. 1.7 - Prob. 139ESCh. 1.7 - Prob. 140ESCh. 1.7 - Prob. 141ESCh. 1.7 - Prob. 142ESCh. 1.7 - Prob. 143ESCh. 1.7 - Prob. 144ESCh. 1.7 - Prob. 145ESCh. 1.7 - Use your calculator to attempt to find the...Ch. 1.7 - In Exercises 147149, perform the indicated...Ch. 1.7 - In Exercises 147149, perform the indicated...Ch. 1.7 - Prob. 149ESCh. 1.7 - Prob. 150ESCh. 1.7 - Prob. 151ESCh. 1.7 - Prob. 152ESCh. 1.8 - Fill in each blank so that the resulting statement...Ch. 1.8 - Fill in each blank so that the resulting statement...Ch. 1.8 - In the remaining items, use the choices below to...Ch. 1.8 - Prob. 4CAVCCh. 1.8 - Prob. 5CAVCCh. 1.8 - Prob. 6CAVCCh. 1.8 - Prob. 7CAVCCh. 1.8 - Prob. 1ESCh. 1.8 - Prob. 2ESCh. 1.8 - In Exercises 114, evaluate each exponential...Ch. 1.8 - In Exercises 114, evaluate each exponential...Ch. 1.8 - In Exercises 114, evaluate each exponential...Ch. 1.8 - Prob. 6ESCh. 1.8 - Prob. 7ESCh. 1.8 - Prob. 8ESCh. 1.8 - In Exercises 114, evaluate each exponential...Ch. 1.8 - In Exercises 114, evaluate each exponential...Ch. 1.8 - In Exercises 114, evaluate each exponential...Ch. 1.8 - Prob. 12ESCh. 1.8 - Prob. 13ESCh. 1.8 - Prob. 14ESCh. 1.8 - Prob. 15ESCh. 1.8 - Prob. 16ESCh. 1.8 - Prob. 17ESCh. 1.8 - Prob. 18ESCh. 1.8 - In Exercises 1528, simplify each algebraic...Ch. 1.8 - In Exercises 1528, simplify each algebraic...Ch. 1.8 - In Exercises 1528, simplify each algebraic...Ch. 1.8 - Prob. 22ESCh. 1.8 - Prob. 23ESCh. 1.8 - Prob. 24ESCh. 1.8 - Prob. 25ESCh. 1.8 - Prob. 26ESCh. 1.8 - Prob. 27ESCh. 1.8 - Prob. 28ESCh. 1.8 - In Exercises 2972, use the order of operations to...Ch. 1.8 - In Exercises 2972, use the order of operations to...Ch. 1.8 - In Exercises 2972, use the order of operations to...Ch. 1.8 - Prob. 32ESCh. 1.8 - Prob. 33ESCh. 1.8 - Prob. 34ESCh. 1.8 - Prob. 35ESCh. 1.8 - Prob. 36ESCh. 1.8 - Prob. 37ESCh. 1.8 - Prob. 38ESCh. 1.8 - In Exercises 2972, use the order of operations to...Ch. 1.8 - In Exercises 2972, use the order of operations to...Ch. 1.8 - In Exercises 2972, use the order of operations to...Ch. 1.8 - Prob. 42ESCh. 1.8 - Prob. 43ESCh. 1.8 - Prob. 44ESCh. 1.8 - Prob. 45ESCh. 1.8 - Prob. 46ESCh. 1.8 - Prob. 47ESCh. 1.8 - Prob. 48ESCh. 1.8 - In Exercises 2972, use the order of operations to...Ch. 1.8 - In Exercises 2972, use the order of operations to...Ch. 1.8 - In Exercises 2972, use the order of operations to...Ch. 1.8 - Prob. 52ESCh. 1.8 - Prob. 53ESCh. 1.8 - Prob. 54ESCh. 1.8 - Prob. 55ESCh. 1.8 - Prob. 56ESCh. 1.8 - Prob. 57ESCh. 1.8 - In Exercises 2972, use the order of operations to...Ch. 1.8 - In Exercises 2972, use the order of operations to...Ch. 1.8 - In Exercises 2972, use the order of operations to...Ch. 1.8 - Prob. 61ESCh. 1.8 - Prob. 62ESCh. 1.8 - Prob. 63ESCh. 1.8 - Prob. 64ESCh. 1.8 - Prob. 65ESCh. 1.8 - Prob. 67ESCh. 1.8 - Prob. 68ESCh. 1.8 - In Exercises 2972, use the order of operations to...Ch. 1.8 - In Exercises 2972, use the order of operations to...Ch. 1.8 - In Exercises 2972, use the order of operations to...Ch. 1.8 - Prob. 72ESCh. 1.8 - Prob. 73ESCh. 1.8 - Prob. 74ESCh. 1.8 - Prob. 75ESCh. 1.8 - Prob. 76ESCh. 1.8 - Prob. 77ESCh. 1.8 - Prob. 78ESCh. 1.8 - In Exercises 7380, evaluate each algebraic...Ch. 1.8 - In Exercises 7380, evaluate each algebraic...Ch. 1.8 - In Exercises 8188, simplify each algebraic...Ch. 1.8 - Prob. 82ESCh. 1.8 - Prob. 83ESCh. 1.8 - Prob. 84ESCh. 1.8 - Prob. 85ESCh. 1.8 - Prob. 86ESCh. 1.8 - Prob. 87ESCh. 1.8 - Prob. 88ESCh. 1.8 - In Exercises 8992, express each sentence as a...Ch. 1.8 - Prob. 90ESCh. 1.8 - Prob. 91ESCh. 1.8 - Prob. 92ESCh. 1.8 - Prob. 93ESCh. 1.8 - Prob. 94ESCh. 1.8 - In Exercises 9396, let x represent the number....Ch. 1.8 - In Exercises 9396, let x represent the number....Ch. 1.8 - Use the appropriate information displayed by the...Ch. 1.8 - Prob. 98ESCh. 1.8 - The data can be described by the following...Ch. 1.8 - The data can be described by the following...Ch. 1.8 - Prob. 101ESCh. 1.8 - Prob. 102ESCh. 1.8 - Prob. 103ESCh. 1.8 - Prob. 104ESCh. 1.8 - Prob. 105ESCh. 1.8 - Prob. 106ESCh. 1.8 - Prob. 107ESCh. 1.8 - Prob. 108ESCh. 1.8 - Prob. 109ESCh. 1.8 - Prob. 110ESCh. 1.8 - Prob. 111ESCh. 1.8 - Prob. 112ESCh. 1.8 - Prob. 113ESCh. 1.8 - Prob. 114ESCh. 1.8 - Prob. 115ESCh. 1.8 - In Exercises 115116, insert parentheses in each...Ch. 1.8 - Prob. 117ESCh. 1.8 - Prob. 118ESCh. 1.8 - Prob. 119ESCh. 1.8 - Prob. 120ESCh. 1.8 - Exercises 120122 will help you prepare for the...Ch. 1.8 - Prob. 122ESCh. 1 - Evaluate for x=6:2+10x .Ch. 1 - Prob. 2MCPCh. 1 - Prob. 3MCPCh. 1 - Prob. 4MCPCh. 1 - Prob. 5MCPCh. 1 - Prob. 6MCPCh. 1 - Prob. 7MCPCh. 1 - Prob. 8MCPCh. 1 - Prob. 9MCPCh. 1 - Prob. 10MCPCh. 1 - Prob. 11MCPCh. 1 - Prob. 12MCPCh. 1 - Prob. 13MCPCh. 1 - Prob. 14MCPCh. 1 - Prob. 15MCPCh. 1 - Prob. 16MCPCh. 1 - Prob. 17MCPCh. 1 - Prob. 18MCPCh. 1 - Prob. 19MCPCh. 1 - Prob. 20MCPCh. 1 - Prob. 21MCPCh. 1 - Prob. 22MCPCh. 1 - Prob. 23MCPCh. 1 - Prob. 24MCPCh. 1 - Prob. 25MCPCh. 1 - Prob. 1RECh. 1 - Prob. 2RECh. 1 - Prob. 3RECh. 1 - Prob. 4RECh. 1 - Prob. 5RECh. 1 - Prob. 6RECh. 1 - Prob. 7RECh. 1 - Prob. 8RECh. 1 - Prob. 9RECh. 1 - Prob. 10RECh. 1 - Prob. 11RECh. 1 - Prob. 12RECh. 1 - Prob. 13RECh. 1 - Prob. 14RECh. 1 - Prob. 15RECh. 1 - Prob. 16RECh. 1 - Prob. 17RECh. 1 - Prob. 18RECh. 1 - Prob. 19RECh. 1 - Prob. 20RECh. 1 - Prob. 21RECh. 1 - Prob. 22RECh. 1 - Prob. 23RECh. 1 - In Exercises 2429, perform the indicated...Ch. 1 - In Exercises 2429, perform the indicated...Ch. 1 - Prob. 26RECh. 1 - Prob. 27RECh. 1 - Prob. 28RECh. 1 - Prob. 29RECh. 1 - Prob. 30RECh. 1 - Prob. 31RECh. 1 - In Exercises 3233, translate from English to an...Ch. 1 - In Exercises 3233, translate from English to an...Ch. 1 - Suppose that the target heart rate, H, in beats...Ch. 1 - Prob. 35RECh. 1 - Prob. 36RECh. 1 - Prob. 37RECh. 1 - Prob. 38RECh. 1 - Prob. 39RECh. 1 - Prob. 40RECh. 1 - Prob. 41RECh. 1 - Give an example of a real number that is not a...Ch. 1 - In Exercises 4346, insert either < or > in the...Ch. 1 - In Exercises 4346, insert either < or > in the...Ch. 1 - Prob. 45RECh. 1 - Prob. 46RECh. 1 - Prob. 47RECh. 1 - Prob. 48RECh. 1 - Prob. 49RECh. 1 - Prob. 50RECh. 1 - Prob. 51RECh. 1 - Use the commutative property of multiplication to...Ch. 1 - In Exercises 5354, use an associative property to...Ch. 1 - In Exercises 5354, use an associative property to...Ch. 1 - Prob. 55RECh. 1 - Prob. 56RECh. 1 - Prob. 57RECh. 1 - Prob. 58RECh. 1 - Prob. 59RECh. 1 - Prob. 60RECh. 1 - Prob. 61RECh. 1 - In Exercises 6263, simplify each algebraic...Ch. 1 - In Exercises 6263, simplify each algebraic...Ch. 1 - The Dead Sea is the lowest elevation on Earth,...Ch. 1 - Prob. 65RECh. 1 - Prob. 66RECh. 1 - Prob. 67RECh. 1 - Prob. 68RECh. 1 - Prob. 69RECh. 1 - Prob. 70RECh. 1 - Prob. 71RECh. 1 - Simplify: 36a82a .Ch. 1 - What is the difference in elevation between a...Ch. 1 - In Exercises 7476, perform the indicated...Ch. 1 - Prob. 75RECh. 1 - Prob. 76RECh. 1 - Prob. 77RECh. 1 - Prob. 78RECh. 1 - Prob. 79RECh. 1 - Prob. 80RECh. 1 - Prob. 81RECh. 1 - Prob. 82RECh. 1 - Prob. 83RECh. 1 - The bar graph shows the number of Americans, in...Ch. 1 - In Exercises 8587, evaluate each exponential...Ch. 1 - In Exercises 8587, evaluate each exponential...Ch. 1 - Prob. 87RECh. 1 - Prob. 88RECh. 1 - Prob. 89RECh. 1 - Prob. 90RECh. 1 - Prob. 91RECh. 1 - Prob. 92RECh. 1 - Prob. 93RECh. 1 - In Exercises 9098, use the order of operations to...Ch. 1 - In Exercises 9098, use the order of operations to...Ch. 1 - In Exercises 9098, use the order of operations to...Ch. 1 - Prob. 97RECh. 1 - Prob. 98RECh. 1 - Prob. 99RECh. 1 - Prob. 100RECh. 1 - Prob. 101RECh. 1 - In Exercises 101102, simplify each algebraic...Ch. 1 - Prob. 103RECh. 1 - In Exercises 110, perform the indicated operation...Ch. 1 - In Exercises 110, perform the indicated operation...Ch. 1 - In Exercises 110, perform the indicated operation...Ch. 1 - In Exercises 110, perform the indicated operation...Ch. 1 - Prob. 5TCh. 1 - Prob. 6TCh. 1 - Prob. 7TCh. 1 - Prob. 8TCh. 1 - Prob. 9TCh. 1 - In Exercises 110, perform the indicated operation...Ch. 1 - In Exercises 1113, simplify each algebraic...Ch. 1 - In Exercises 1113, simplify each algebraic...Ch. 1 - Prob. 13TCh. 1 - Prob. 14TCh. 1 - Prob. 15TCh. 1 - Find the absolute value: |12.8| .Ch. 1 - Prob. 17TCh. 1 - Prob. 18TCh. 1 - Prob. 19TCh. 1 - Use the associative property of multiplication to...Ch. 1 - Use the distributive property to rewrite without...Ch. 1 - What is the difference in elevation between a...Ch. 1 - Prob. 23TCh. 1 - Prob. 24TCh. 1 - Prob. 25TCh. 1 - Prob. 26TCh. 1 - Prob. 27TCh. 1 - Prob. 28TCh. 1 - Prob. 29T
Knowledge Booster
Background pattern image
Algebra
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, algebra and related others by exploring similar questions and additional content below.
Similar questions
SEE MORE QUESTIONS
Recommended textbooks for you
Text book image
Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL
Text book image
Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill
Text book image
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning
Text book image
College Algebra
Algebra
ISBN:9781337282291
Author:Ron Larson
Publisher:Cengage Learning
Text book image
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
SEE MORE TEXTBOOKS
What is a Linear Equation in One Variable?; Author: Don't Memorise;https://www.youtube.com/watch?v=lDOYdBgtnjY;License: Standard YouTube License, CC-BY
Linear Equation | Solving Linear Equations | What is Linear Equation in one variable ?; Author: Najam Academy;https://www.youtube.com/watch?v=tHm3X_Ta_iE;License: Standard YouTube License, CC-BY