
(a)
To show: The stationary line is at distance of
(a)
Answer to Problem 44CP
The distance at which stationary line lie is
Explanation of Solution
Given info: The angle made by the roof with the horizontal plane is
Consider the figure given below.
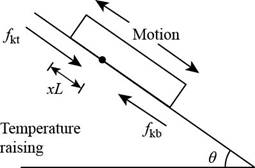
Figure 1
Consider that
The normal force on the lower part of the plane is,
Here,
The force due to gravity is,
The equation for the
The equation for the downward force is,
The force equation for the plate is,
Further, solve for
The distance of the stationary line below the top edge is,
Conclusion:
Therefore, the distance at which stationary line lie is
(b)
To show: The stationary line is at that same distance above the bottom edge of the plate.
(b)
Answer to Problem 44CP
The stationary line is at that same distance above the bottom edge of the plate.
Explanation of Solution
Given info: The angle made by the roof with the horizontal plane is
Consider the figure given below.
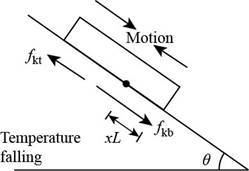
Figure 2
With the temperature falling, the plate contracts faster than the roof. The upper part slides down and feels an upward frictional force,
Then the force equation remains same as in part (a) and the stationary line is above the bottom edge by,
Conclusion:
Therefore, it is proved that the stationary line is at that same distance above the bottom edge of the plate.
(c)
To show: The plate steps down the roof like an inchworm moving each day by the distance
(c)
Answer to Problem 44CP
The distance by which the plate steps down the roof like an inchworm moving each day is
Explanation of Solution
Given info: The angle made by the roof with the horizontal plane is
Consider the figure given below.
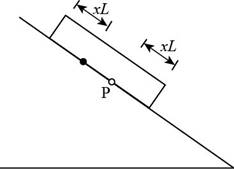
Figure 3
Consider the plate at dawn, as the temperature starts to rise. As in part (a), a line at distance
In the above figure, the point
The change in the length of the plate is,
The change in the length of the roof is,
The point on the roof originally under point
When the temperature drops, point
The displacement for a day is,
Substitute
Conclusion:
Therefore, the distance by which the plate steps down the roof like an inchworm moving each day is
(d)
The distance an aluminum plate moves each day.
(d)
Answer to Problem 44CP
The distance an aluminum plate moves each day is
Explanation of Solution
Given info: The angle made by the roof with the horizontal plane is
The length of the plate is
The coefficient of linear expansion for aluminum is
The formula for the displacement for a day is,
Substitute
Conclusion:
Therefore, the distance an aluminum plate moves each day is
(e)
To explain: The effect on the plate if the expansion coefficient of the plate is less than the expansion coefficient of the roof.
(e)
Answer to Problem 44CP
The plate creeps down the roof each day by an amount given by
Explanation of Solution
Given info: The angle made by the roof with the horizontal plane is
If
The figure I, applies to the temperature falling and figure II applies to temperature rising. A point on the plate
The plate creeps down the roof each day by an amount given by,
Conclusion:
Therefore, the plate creeps down the roof each day by an amount given by
Want to see more full solutions like this?
Chapter 18 Solutions
Bundle: Physics For Scientists And Engineers With Modern Physics, 10th + Webassign Printed Access Card For Serway/jewett's Physics For Scientists And Engineers, 10th, Multi-term
- In a scene from The Avengers (the first one) Black Widow is boosted directly upwards by Captain America, where she then grabs on to a Chitauri speeder that is 15.0 feet above her and hangs on. She is in the air for 1.04 s. A) With what initial velocity was Black Widow launched? 1 m = 3.28 ft B) What was Black Widow’s velocity just before she grabbed the speeder? Assume upwards is the positive direction.arrow_forwardIn Dark Souls 3 you can kill the Ancient Wyvern by dropping on its head from above it. Let’s say you jump off the ledge with an initial velocity of 3.86 mph and spend 1.72 s in the air before hitting the wyvern’s head. Assume the gravity is the same as that of Earth and upwards is the positive direction. Also, 1 mile = 1609 m. A) How high up is the the ledge you jumped from as measured from the wyvern’s head? B) What is your velocity when you hit the wyvern?arrow_forwardA) If Yoshi flings himself downwards at 9.76 miles per hour to hit an enemy 10.5 m below him, how fast is Yoshi traveling when he hits the enemy? 1 mile = 1609 marrow_forward
 Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning





