Chapter 18, Problem 41E

Program Plan Intro

Check digit:

• The digits in the number are added together, and the unit digit of the result is called as check digit, which is used for error detection.
• The unit’s digit of that sum is stored with the number.
• The additional digit is used along with the check digit to find out the transposition error, and it can be found out by the sum of even digits or odd digits in the number.

For example,

Consider the number 3422.

It is stored as 3422-16.

• Count the numbers from left to right; it produces the sum of the digits as 11.
• Here, “1” is the unit’s digit of the sum of all the digits, which is called as check bit.
• “6” is the unit’s digit of the sum of the second and fourth digits (4+2 = 6), which is the additional digit used along with the check digit.
• While storing the above number 3422-16, if “2” is corrupted by “4” and “4” is corrupted by “2”, it leads to a transposition error. So, the number is received as 3242-16 ,
  • By adding the number, it produces the check digit as “1” and it produces the additional digit as “4”.
  • But the received additional digit is “6”. Hence, it is clear that the received number is corrupted.

Explanation of Solution

a.

Find the additional digit using the sum of even digits for “1066” numbers:

The additional digit (using the sum of even digits) for the number 1066 can be determined by the following steps:

Check digit:

• Step 1: Count the given number from left to right.

• Step 2: From the above diagram, the sum of digits produces the result as 13.
• Step 3: The unit’s place in the sum represents the check digit. Thus, “3” is in the unit’s place.
• Step 4: Therefore, check digit for the number 1066 is 3.

Additional digit:

• Step 1: In the given number 1066, take the numbers from the even position from left to right.

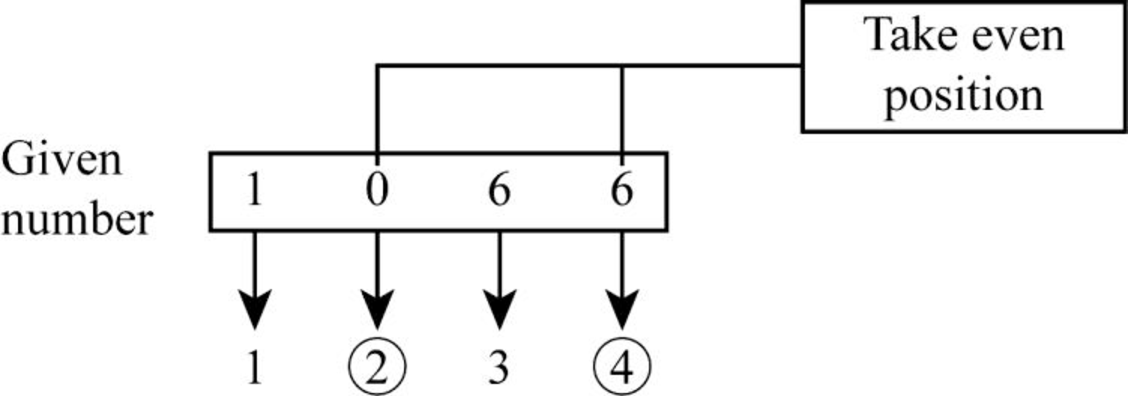
• Step 2: From the above diagram, it is clear that the number “0” on second position and the number “6” on fourth position are the even position numbers.
• Step 3: The sum of digits produces the result as “6” (0+6 = 6).

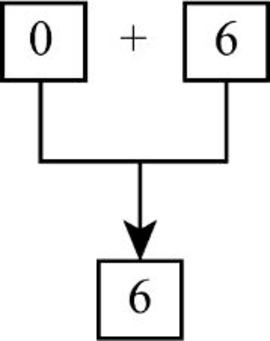
• Step 4: Hence, “6” in the unit’s place is the additional digit used along with the check digit.

Therefore, additional digit used along with the check digit “3” for the number 1066 is “6”.

Explanation of Solution

b.

Find the additional digit using the sum of even digits for “1498” numbers:

The additional digit (using the sum of even digits) for the number 1498 can be determined by the following steps:

Check digit:

• Step 1: Count the given number from left to right.

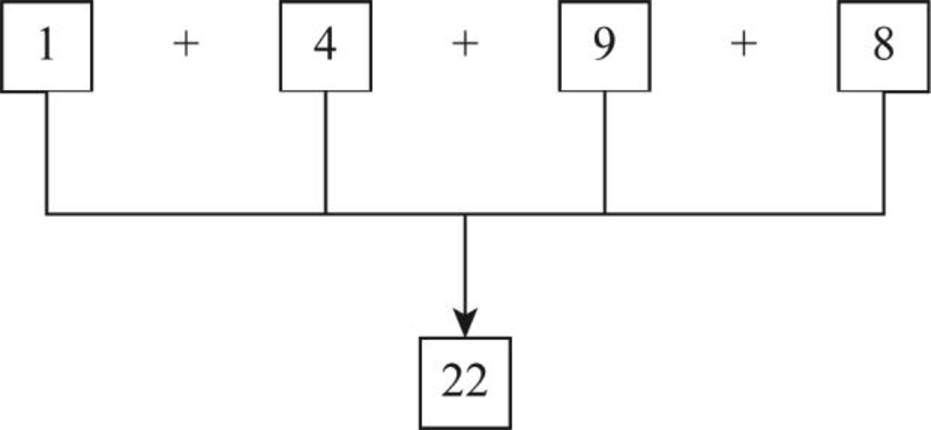
• Step 2: From the above diagram, the sum of digits produces the result as 22.
• Step 3: The unit’s place in the sum represents the check digit. Thus, “2” is in the unit’s place.
• Step 4: Therefore, check digit for the number 1498 is 2.

Additional digit:

• Step 1: In the given number 1498, take the numbers from the even position from left to right.

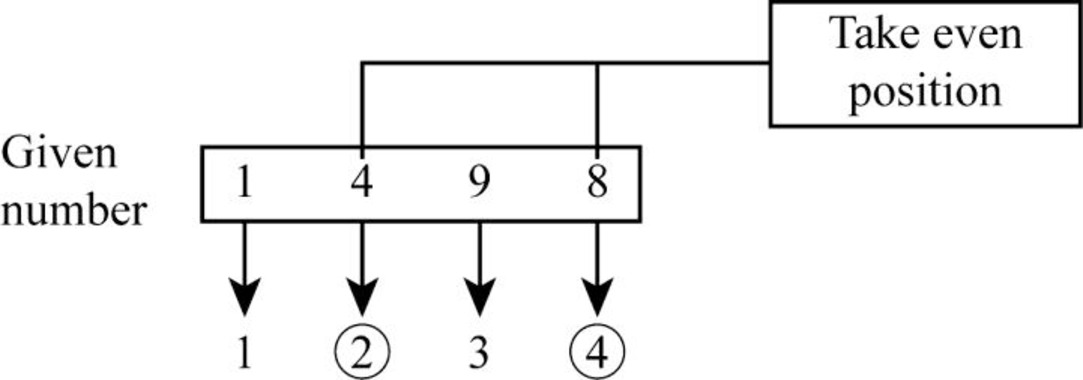
• Step 2: From the above diagram, it clearly states that the number “4” on second position and the number “8” on fourth position are the even position numbers.
• Step3: The sum of digits produces the result as “12” (4+8 = 12).

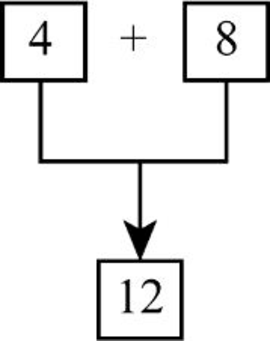
• Step4: Hence, “2” in the unit’s place is the additional digit used along with the check digit.

Therefore, additional digit used along with the check digit “2” for the number 1498 is “2”.

Explanation of Solution

c.

Find the additional digit using the sum of even digits for “1668” numbers:

The additional digit (using the sum of even digits) for the number 1668 can be determined by the following steps:

Check digit:

• Step 1: Count the given number from left to right.

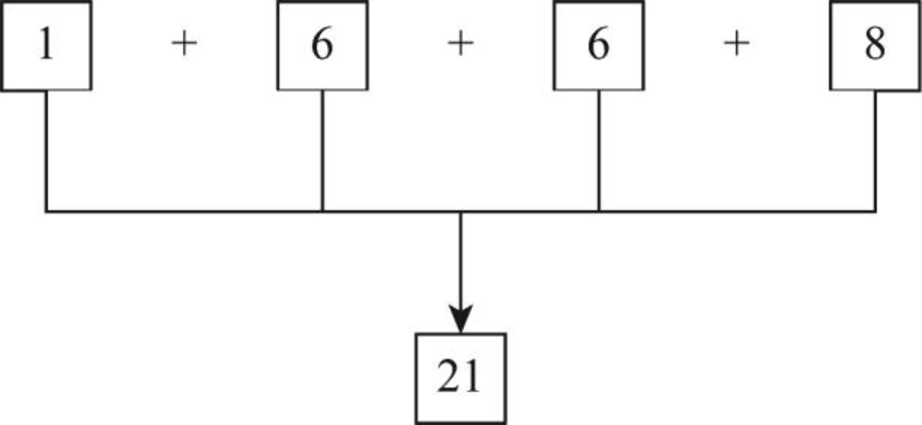
• Step 2: From the above diagram, the sum of digits produces the result as 21.
• Step 3: The unit’s place in the sum represents the check digit. Thus, “1” is in the unit’s place.
• Step 4: Therefore, check digit for the number 1668 is 1.

Additional digit:

• Step 1: In the given number 1668, take the numbers from the even position from left to right.

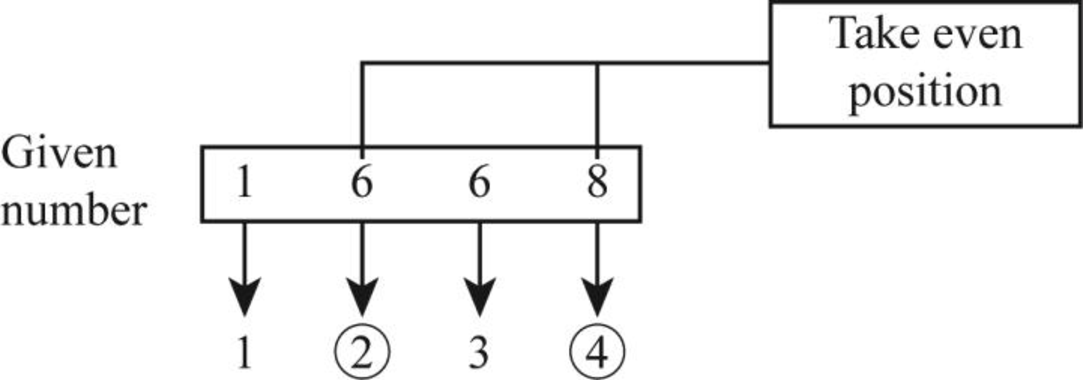
• Step 2: From the above diagram, it is clear that the number “6” on second position and the number “8” on fourth position are the even position numbers.
• Step 3: The sum of digits produces the result as “14” (6+8 = 14).

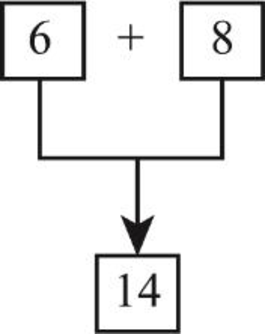
• Step 4: Hence, “4” in the unit’s place is the additional digit used along with the check digit.

Therefore, additional digit used along with the check digit “1” for the number 1668 is “4”.

Explanation of Solution

d.

Find the additional digit using the sum of even digits for “2001” numbers:

The additional digit (using the sum of even digits) for the number 2001 can be determined by the following steps:

Check digit:

• Step 1: Count the given number from left to right.

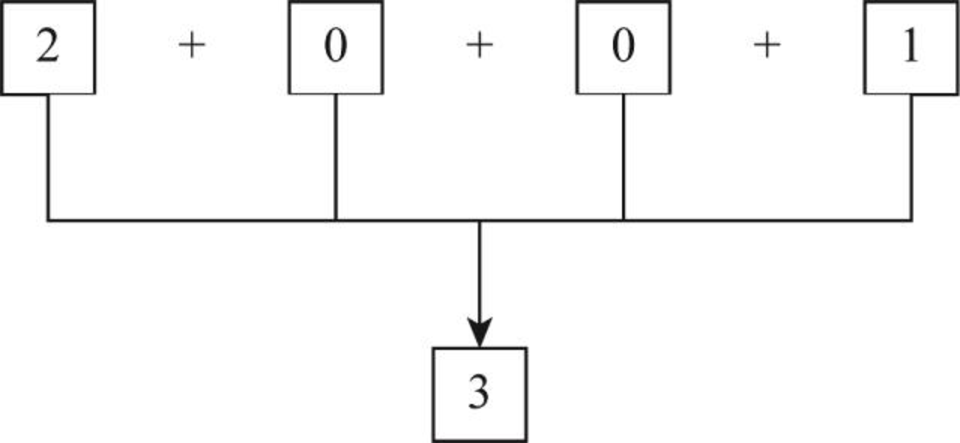
• Step 2: From the above diagram, the sum of digits produces the result as 3.
• Step 3: The unit’s place in the sum represents the check digit. Thus, “3” is in the unit’s place.
• Step 4: Therefore, check digit for the number 2001 is 3.

Additional digit:

• Step 1: In the given number 2001, take the numbers from the even position from left to right.

• Step 2: From the above diagram, it is clear that the number “0” on second position and the number “1” on fourth position are the even position numbers.
• Step 3: The sum of digits produces the result as “1” (0+1 = 1).

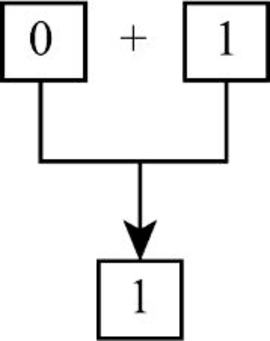
• Step 4: Hence, “1” in the unit’s place is the additional digit used along with the check digit.

Therefore, additional digit used along with the check digit “3” for the number 2001 is “1”.

Explanation of Solution

e.

Find the additional digit using the sum of even digits for “4040” numbers:

The additional digit (using the sum of even digits) for the number 4040 can be determined by the following steps:

Check digit:

• Step 1: Count the given number from left to right.

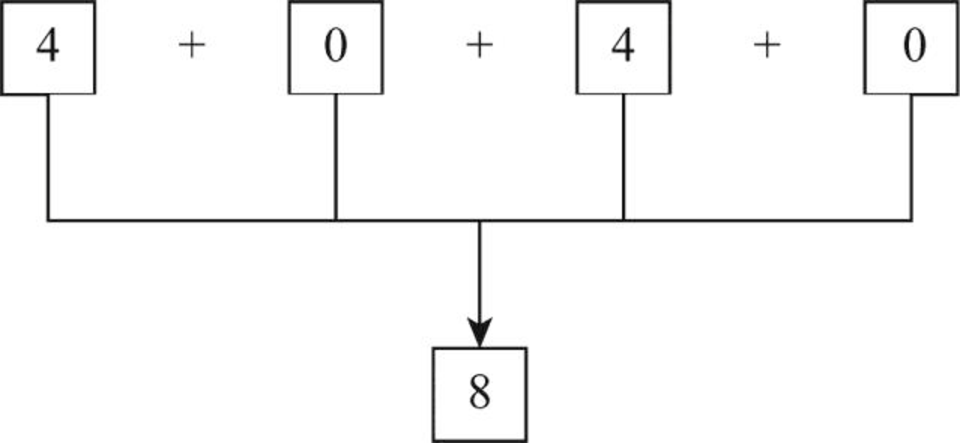
• Step 2: From the above diagram, the sum of digits produces the result as 8.
• Step 3: The unit’s place in the sum represents the check digit. Thus, “8” is in the unit’s place.
• Step 4: Therefore, check digit for the number 4040 is 8.

Additional digit:

• Step 1: In the given number 4040, take the numbers from the even position from left to right.

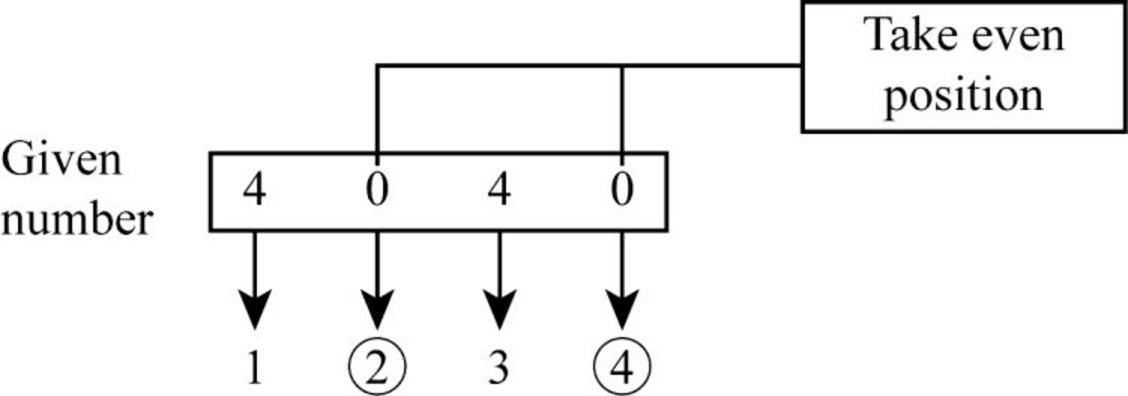
• Step 2: From the above diagram, it is clear that the number “0” on second position and the number “8” on fourth position are the even position numbers.
• Step3: The sum of digits produces the result as “0” (0+0 = 0).

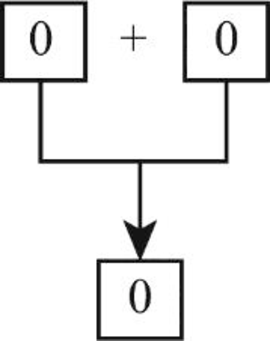
• Step 4: Hence, “0” in the unit’s place is the additional digit used along with the check digit.

Therefore, additional digit used along with the check digit “8” for the number 4040 is “0”.