
Concept explainers
A standing wave is described by the wave function
where x and y are in meters and t is in seconds. (a) Prepare graphs showing y as a function of x for five instants: t = 0, 5 ms, 10 ms, 15 ms, and 20 ms. (b) From the graph, identify the wavelength of the wave and explain how to do so. (c) From the graph, identify the frequency of the wave and explain how to do so. (d) From the equation, directly identify the wavelength of the wave and explain bow to do so. (e) From the equation, directly identify the frequency and explain how to do so.
(a)
To draw: The graphs showing
Answer to Problem 10P
The graph of
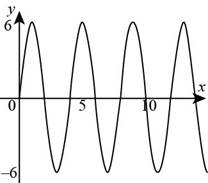
Figure (1)
The graph of
Figure (2)
The graph of
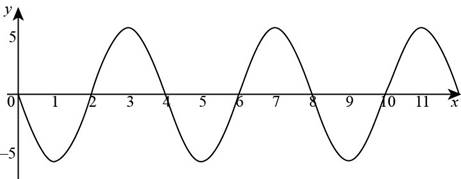
Figure (3)
The graph of
Figure (4)
The graph of

Figure (5)
Explanation of Solution
Introduction:
The values of
Explanation:
Given info: The sinusoidal waves function is,
For
Substitute
The graph of
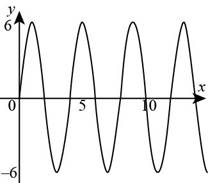
Figure (1)
For
Substitute
The graph of

Figure (2)
For
Substitute
The graph of
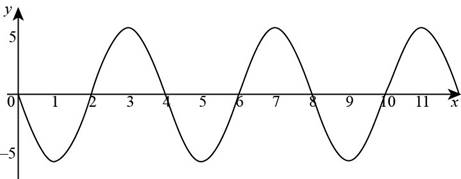
Figure (3)
For
Substitute
The graph of

Figure (4)
For
Substitute
The graph of
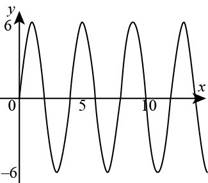
Figure (5)
(b)
Answer to Problem 10P
Explanation of Solution
Given info: The sinusoidal waves function is
The distance between the two-crest point or two trough point is called the wavelength of the wave.
From the figure (1), the distance between the two crest point is
Conclusion:
Therefore, the wavelength of the wave is
(c)
Answer to Problem 10P
Explanation of Solution
Given info: The sinusoidal waves function is
Compare the equation (1) with
The frequency of the wave is,
Substitute
Conclusion:
Therefore, the frequency of the wave is
(d)
Answer to Problem 10P
Explanation of Solution
Given info: The sinusoidal waves function is
Compare the equation (1) with
The frequency of the wave is,
Substitute
Conclusion:
Therefore, the wavelength of the wave is
(e)
Answer to Problem 10P
Explanation of Solution
Given info: The sinusoidal waves function is
Compare the equation (1) with
The frequency of the wave is,
Substitute
Conclusion:
Therefore, the frequency of the wave is
Want to see more full solutions like this?
Chapter 17 Solutions
Physics for Scientists and Engineers
- 1. A charge of -25 μC is distributed uniformly throughout a spherical volume of radius 11.5 cm. Determine the electric field due to this charge at a distance of (a) 2 cm, (b) 4.6 cm, and (c) 25 cm from the center of the sphere. (a) = = (b) E = (c)Ẻ = = NC NC NCarrow_forward1. A long silver rod of radius 3.5 cm has a charge of -3.9 ис on its surface. Here ŕ is a unit vector ст directed perpendicularly away from the axis of the rod as shown in the figure. (a) Find the electric field at a point 5 cm from the center of the rod (an outside point). E = N C (b) Find the electric field at a point 1.8 cm from the center of the rod (an inside point) E=0 Think & Prepare N C 1. Is there a symmetry in the charge distribution? What kind of symmetry? 2. The problem gives the charge per unit length 1. How do you figure out the surface charge density σ from a?arrow_forward1. Determine the electric flux through each surface whose cross-section is shown below. 55 S₂ -29 S5 SA S3 + 9 Enter your answer in terms of q and ε Φ (a) s₁ (b) s₂ = -29 (C) Φ զ Ερ (d) SA = (e) $5 (f) Sa $6 = II ✓ -29 S6 +39arrow_forward
- No chatgpt pls will upvotearrow_forwardthe cable may break and cause severe injury. cable is more likely to break as compared to the [1] ds, inclined at angles of 30° and 50° to the vertical rings by way of a scaled diagram. [4] I 30° T₁ 3cm 3.8T2 cm 200 N 50° at it is headed due North and its airspeed indicat 240 km/h. If there is a wind of 100 km/h from We e relative to the Earth? [3]arrow_forwardCan you explain this using nodal analysis With the nodes I have present And then show me how many KCL equations I need to write, I’m thinking 2 since we have 2 dependent sourcesarrow_forward
- The shear leg derrick is used to haul the 200-kg net of fish onto the dock as shown in. Assume the force in each leg acts along its axis. 5.6 m. 4 m- B Part A Determine the compressive force along leg AB. Express your answer to three significant figures and include the appropriate units. FAB = Value Submit Request Answer Part B Units ? Determine the compressive force along leg CB. Express your answer to three significant figures and include the appropriate units. FCB= Value Submit Request Answer Part C ? Units Determine the tension in the winch cable DB. Express your answer with the appropriate units. 2marrow_forwardPart A (Figure 1) shows a bucket suspended from a cable by means of a small pulley at C. If the bucket and its contents have a mass of 10 kg, determine the location of the pulley for equilibrium. The cable is 6 m long. Express your answer to three significant figures and include the appropriate units. Figure 4 m B НА x = Value Submit Request Answer Provide Feedback < 1 of 1 T 1 m Units ?arrow_forwardThe particle in is in equilibrium and F4 = 165 lb. Part A Determine the magnitude of F1. Express your answer in pounds to three significant figures. ΑΣΦ tvec F₁ = Submit Request Answer Part B Determine the magnitude of F2. Express your answer in pounds to three significant figures. ΑΣΦ It vec F2 = Submit Request Answer Part C Determine the magnitude of F3. Express your answer in pounds to three significant figures. ? ? lb lb F₂ 225 lb 135° 45° 30° -60°-arrow_forward
 Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University
University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University An Introduction to Physical SciencePhysicsISBN:9781305079137Author:James Shipman, Jerry D. Wilson, Charles A. Higgins, Omar TorresPublisher:Cengage Learning
An Introduction to Physical SciencePhysicsISBN:9781305079137Author:James Shipman, Jerry D. Wilson, Charles A. Higgins, Omar TorresPublisher:Cengage Learning Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill
Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill





