Chapter 16.R, Problem 26E

To determine

(a)

To find:

An equation of the tangent plane at the point $\left(4, -2, 1\right)$ to the given parametric surface $S$

Solution:

$x+4y+4z=0$

Explanation:

1) Concept:

The equation of the tangent plane is

$\left(r-a\right)·n=0$

Where $a$ be theposition vector of a point on the plane and $n=r_u\times r_v$ is the normal vector to the plane.

2) Given:

The parametric surface $S$ is

$r\left(u, v\right)=v^{2}i-uvj+u^{2}k, 0\le u\le 3, -3\le v\le 3$

3) Calculations:

The parametric surface $S$ is

$r\left(u, v\right)=v^{2}i-uvj+u^{2}k, 0\le u\le 3, -3\le v\le 3$

To find the tangent vectors $r_u and{r}_v$

$r_u=0-vj+2uk=-vj+2uk$

$r_v=2v-uj+0=2v-uj$

The normal vector to the tangent plane is $r_u\times r_v$

$r_u\times r_v=\left|\begin{array}{ccc}i& j& k\\ 0& -v& 2u\\ 2v& -u& 0\end{array}\right|$

$r_u\times r_v=2u^{2}i+4uvj+2v^{2}k$

This can be written as,

$r_u\times r_v=u^{2}i+2uvj+v^{2}k$

At the point $\left(4, -2, 1\right)$, corresponds to $u=\pm 1 and v=\pm 2$

For $u=1 and v=2$, the normal vectors becomes,

$r_u\times r_v={\left(1\right)}^{2}i+2\left(1\right)\left(2\right)j+{\left(2\right)}^{2}k$

$n=r_u\times r_v=i+4j+4k$

The position vector of a point $\left(4, -2, 1\right)$ on the plane is $a=4i-2j+k$

The equation of the tangent plane is

$\left(r-a\right)·n=0$

$\left(\left(x-4\right)i+\left(y+2\right)j+\left(z-1\right)k\right)·\left(i+4j+4k\right)=0$

$\left(x-4\right)\left(1\right)+\left(y+2\right)\left(4\right)+\left(z-1\right)\left(4\right)=0$

$x-4+4y+8+4z-4=0$

$x+4y+4z=0$

This is the equation of the tangent plane

Conclusion:

Thus, anequation of the tangent plane at the point $\left(4, -2, 1\right)$ to the given parametric surface $S$ is

$x+4y+4z=0$

(b)

To draw:

The graph of surface $S$ and the tangent plane found in part (a)’

Solution:

Explanation:

1) Concept:

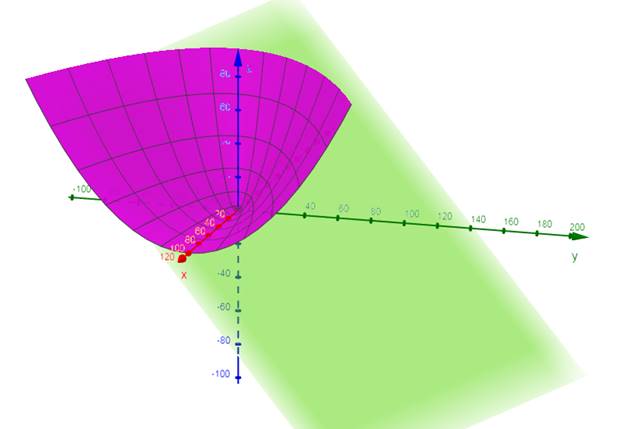
To draw the graph of surface $S$ and the tangent plane by using the computer

2) Calculations:

The parametric surface $S$ is

$r\left(u, v\right)=v^{2}i-uvj+u^{2}k, 0\le u\le 3, -3\le v\le 3$

The equation of the tangent plane is

$x+4y+4z=0$

To draw the graph of surface $S$ and the tangent plane by using computer

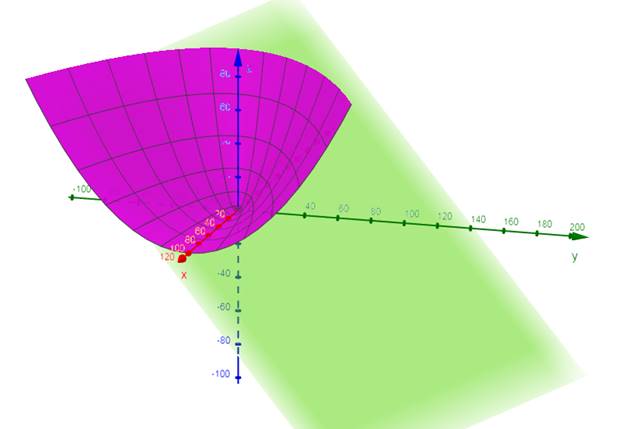
Conclusion:

The graph of surface $S$ and the tangent plane found in part (a) is

(c)

To set up:

An integral for the surface area $S$

Solution:

$2{\int }_0^3{\int }_{-3}^3\sqrt{u^4+4u^2{v}^2+v^4}dv du$

Explanation:

1) Concept:

If a smooth parametric surface $S$ is given by the equation

$r\left(u, v\right)=x\left(u, v\right)i+y\left(u, v\right)j+z\left(u, v\right)k, \left(u, v\right)\in D$

And $S$ is covered just once as $\left(u, v\right)$ ranges throught the parameter domain $D,$ then the surface area of $S$ is

$A\left(S\right)={\iint }_D^{\square }\left|r_u\times r_v\right|dA$

Where $r_u=\frac{\partial x}{\partial u}i+\frac{\partial y}{\partial u}j+\frac{\partial z}{\partial u}k \&r_v=\frac{\partial x}{\partial v}i+\frac{\partial y}{\partial v}j+\frac{\partial z}{\partial v}k$‘

2) Given:

The parametric surface $S$ is

$r\left(u, v\right)=v^{2}i-uvj+u^{2}k, 0\le u\le 3, -3\le v\le 3$

3) Calculations:

The parametric surface $S$ is

$r\left(u, v\right)=v^{2}i-uvj+u^{2}k, 0\le u\le 3, -3\le v\le 3$

The surface area $S$ is

$A\left(S\right)={\iint }_D^{\square }\left|r_u\times r_v\right|dA$

$={\int }_0^3{\int }_{-3}^3\sqrt{{\left(2u^2\right)}^2+{\left(4uv\right)}^2+{\left(2v^2\right)}^2}dv du$

$={\int }_0^3{\int }_{-3}^3\sqrt{4u^4+16u^2{v}^2+4v^4}dv du$

$A\left(S\right)=2{\int }_0^3{\int }_{-3}^3\sqrt{u^4+4u^2{v}^2+v^4}dv du$

Conclusion:

 An integral for the surface area $S$ is

$A\left(S\right)=2{\int }_0^3{\int }_{-3}^3\sqrt{u^4+4u^2{v}^2+v^4}dv du$

(d)

To find:

${\iint }_S^{\square }F·dS$ Correct to four decimal places by using CAS.

Solution:

$\approx 1524.0190$

Explanation:

1) Concept:

${\iint }_S^{\square }F·dS={\iint }_D^{\square }F·\left(r_u\times r_v\right)dA$

2) Given:

$F\left(x, y, z\right)=\frac{z^2}{1+x^2}i+\frac{x^2}{1+y^2}j+\frac{y^2}{1+z^2}k$

3) Calculations:

From the part (a),

$r_u\times r_v=2u^{2}i+4uvj+2v^{2}k$

$F=〈\frac{z^2}{1+x^2}, \frac{x^2}{1+y^2}, \frac{y^2}{1+z^2}〉$

$F=〈\frac{{\left(u^2\right)}^2}{1+{\left(v^2\right)}^2}, \frac{{\left(v^2\right)}^2}{1+{\left(-uv\right)}^2}, \frac{{\left(-uv\right)}^2}{1+{\left(u^2\right)}^2}〉$

$F=〈\frac{u^4}{1+v^4}, \frac{v^4}{1+u^2{v}^2}, \frac{u^2{v}^2}{1+u^4}〉$

The surface integral is,

${\iint }_S^{\square }F·dS={\iint }_D^{\square }F·\left(r_u\times r_v\right)dA$

${\iint }_S^{\square }F·dS={\int }_0^3{\int }_{-3}^{3}F·\left(r_u\times r_v\right)dA$

To find $F·\left(r_u\times r_v\right)$

$F·\left(r_u\times r_v\right)=〈\frac{u^4}{1+v^4}, \frac{v^4}{1+u^2{v}^2}, \frac{u^2{v}^2}{1+u^4}〉·〈2u^2, 4uv ,2v^2〉$

$=〈\frac{2u^6}{1+v^4}, \frac{4u{v}^5}{1+u^2{v}^2}, \frac{2u^2{v}^4}{1+u^4}〉$

Substitute this value insurface integral

${\iint }_S^{\square }F·dS={\int }_0^3{\int }_{-3}^3\left(\frac{2u^6}{1+v^4}+\frac{4u{v}^5}{1+u^2{v}^2}+\frac{2u^2{v}^4}{1+u^4}\right)dA$

Use the command in Mathematica

$\mathrm{N}\mathrm{I}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{e}\left[\right((2*u^6)/(1+v^4))+((4*u*v^5)/(1+v^2*u^2))+((2*u^2*v^4)/(1+u^4)),\{u,\mathrm{0,3}\},\{v,-\mathrm{3,3}\left\}\right]$

$=1524.01900152155$

Therefore,

${\iint }_S^{\square }F·dS\approx 1524.0190$

Conclusion:

${\iint }_S^{\square }F·dS\approx 1524.0190$