UD CALC (241 ONLY) W/1 TERM ACCESS >IB
UD CALC (241 ONLY) W/1 TERM ACCESS >IB
8th Edition
ISBN: 9781337051545
Author: Stewart
Publisher: CENGAGE C
bartleby

Videos

Textbook Question
Book Icon
Chapter 16.1, Problem 32E

Match the functions f with the plots of their gradient vector fields labeled I–IV. Give reasons for your choices.

f ( x , y ) = sin x 2 + y 2

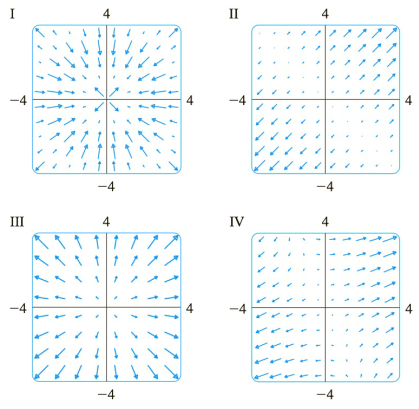
Chapter 16.1, Problem 32E, Match the functions f with the plots of their gradient vector fields labeled IIV. Give reasons for

Expert Solution & Answer
Check Mark
bartleby

Trending nowThis is a popular solution!

See solution
Check out sample textbook solution
Blurred answer
Previous
Chapter 16.1, Problem 31E
Next
Chapter 16.1, Problem 33E
Students have asked these similar questions
25-30. Normal and tangential components For the vector field F and curve C, complete the following: a. Determine the points (if any) along the curve C at which the vector field F is tangent to C. b. Determine the points (if any) along the curve C at which the vector field F is normal to C. c. Sketch C and a few representative vectors of F on C. 25. F = (2½³, 0); c = {(x, y); y − x² = 1} 26. F = x (23 - 212) ; C = {(x, y); y = x² = 1}) , 2 27. F(x, y); C = {(x, y): x² + y² = 4} 28. F = (y, x); C = {(x, y): x² + y² = 1} 29. F = (x, y); C = 30. F = (y, x); C = {(x, y): x = 1} {(x, y): x² + y² = 1}
٣/١ B msl kd 180 Ka, Sin (1) I sin () sin(30) Sin (30) اذا ميريد شرح الكتب بس 0 بالفراغ 3) Cos (30) 0.866 4) Rotating 5) Synchronous speed, 120 x 50 G 5005 1000 s = 1000-950 Copper bosses 5kW Rotor input 5 0.05 : loo kw 6) 1 /0001 ined sove in peaper I need a detailed solution on paper please وه اذا ميريد شرح الكتب فقط ١٥٠ DC 7) rotor a ' (y+xlny + xe*)dx + (xsiny + xlnx + dy = 0. Q1// Find the solution of: ( 357
۳/۱ R₂ = X2 2) slots per pole per phase 3/31 B. 180 msl Kas Sin (I) 1sin() sin(30) Sin (30) اذا ميريد شرح الكتب بس 0 بالفراغ 3) Cos (30): 0.866 4) Rotating 5) Synchronous speeds 120×50 looo G 1000-950 1000 Copper losses 5kw Rotor input 5 loo kw 0.05 6) 1 اذا ميريد شرح الكتب فقط look 7) rotor DC ined sove in peaper I need a detailed solution on paper please 0 64 Find the general solution of the following equations: QI//y(4)-16y= 0. Find the general solution of the following equations: Q2ll yll-4y/ +13y=esinx.

Chapter 16 Solutions

UD CALC (241 ONLY) W/1 TERM ACCESS >IB

Ch. 16.1 - 110 Sketch the vector field F by drawing a diagram...Ch. 16.1 - Sketch the vector field F by drawing a diagram...Ch. 16.1 - Sketch the vector field F by drawing a diagram...Ch. 16.1 - 110 Sketch the vector field F by drawing a diagram...Ch. 16.1 - 110 Sketch the vector field F by drawing a diagram...Ch. 16.1 - 110 Sketch the vector field F by drawing a diagram...Ch. 16.1 - Prob. 7ECh. 16.1 - Prob. 8ECh. 16.1 - Prob. 9ECh. 16.1 - Prob. 10E
Ch. 16.1 - Prob. 11ECh. 16.1 - Match the vector fields F with the plots labelled...Ch. 16.1 - Match the vector fields F with the plots labelled...Ch. 16.1 - Match the vector fields F with the plots labeled...Ch. 16.1 - Match the vector fields F on 3 with the plots...Ch. 16.1 - Match the vector fields F on 3 with the plots...Ch. 16.1 - Match the vector fields F on 3 with the plots...Ch. 16.1 - Match the vector fields F on 3 with the plots...Ch. 16.1 - Prob. 19ECh. 16.1 - Prob. 20ECh. 16.1 - Prob. 21ECh. 16.1 - Find the gradient vector field of f. f(s,t)=2s+3tCh. 16.1 - Find the gradient vector field of f....Ch. 16.1 - Find the gradient vector field of f....Ch. 16.1 - Find the gradient vector field f of f and sketch...Ch. 16.1 - Find the gradient vector field f of f and sketch...Ch. 16.1 - Prob. 27ECh. 16.1 - Plot the gradient vector field of f together with...Ch. 16.1 - Match the functions f with the plots of their...Ch. 16.1 - Match the functions f with the plots of their...Ch. 16.1 - Match the functions f with the plots of their...Ch. 16.1 - Match the functions f with the plots of their...Ch. 16.1 - A particle moves in a velocity field...Ch. 16.1 - Prob. 34ECh. 16.1 - The flow lines or streamlines of a vector field...Ch. 16.1 - a Sketch the vector field F(x,y)=i+xj and then...Ch. 16.2 - Evaluate the line integral, where C is the given...Ch. 16.2 - Evaluate the line integral, where C is the given...Ch. 16.2 - Evaluate the line integral, where C is the given...Ch. 16.2 - Prob. 4ECh. 16.2 - Evaluate the line integral, where C is the given...Ch. 16.2 - Evaluate the line integral, where C is the given...Ch. 16.2 - Evaluate the line integral, where C is the given...Ch. 16.2 - Evaluate the line integral, where C is the given...Ch. 16.2 - Evaluate the line integral, where C is the given...Ch. 16.2 - Evaluate the line integral, where C is the given...Ch. 16.2 - Evaluate the line integral, where C is the given...Ch. 16.2 - Evaluate the line integral, where C is the given...Ch. 16.2 - Evaluate the line integral, where C is the given...Ch. 16.2 - Prob. 14ECh. 16.2 - Evaluate the line integral, where C is the given...Ch. 16.2 - Prob. 16ECh. 16.2 - Let F be the vector fields shown in the figure. a...Ch. 16.2 - The figure shows a vector field F and two curves...Ch. 16.2 - Prob. 19ECh. 16.2 - Prob. 20ECh. 16.2 - Prob. 21ECh. 16.2 - Evaluate the line integral CFdr, where C is given...Ch. 16.2 - Prob. 23ECh. 16.2 - Prob. 24ECh. 16.2 - Prob. 25ECh. 16.2 - Prob. 26ECh. 16.2 - Use a graph of the vector field F and the curve C...Ch. 16.2 - Use a graph of the vector field F and the curve C...Ch. 16.2 - a Evaluate the line integral CFdr, where...Ch. 16.2 - a Evaluate the line integral CFdr, where...Ch. 16.2 - Find the exact value of Cx3y3zds, where C is the...Ch. 16.2 - a Find the work done by the force field...Ch. 16.2 - A thin wire is bent into the shape of a semicircle...Ch. 16.2 - A thin wire has the shape of the first-quadrant...Ch. 16.2 - a Write the formulas similar to Equations 4 for...Ch. 16.2 - Find the mass and center of mass of a wire in the...Ch. 16.2 - Prob. 37ECh. 16.2 - Prob. 38ECh. 16.2 - Find the work done by the force field...Ch. 16.2 - Find the work done by the force field...Ch. 16.2 - Prob. 41ECh. 16.2 - Prob. 42ECh. 16.2 - Prob. 43ECh. 16.2 - An object with mass m moves with position function...Ch. 16.2 - A 160-lb man carries a 25-lb can of paint up a...Ch. 16.2 - Prob. 46ECh. 16.2 - a Show that a constant force field does zero work...Ch. 16.2 - Prob. 48ECh. 16.2 - If C is a smooth curve given by a vector function...Ch. 16.2 - Prob. 50ECh. 16.2 - An object moves along the curve C shown in the...Ch. 16.2 - Experiments show that a steady current I in a long...Ch. 16.3 - The figure shows a curve C and a contour map of a...Ch. 16.3 - Prob. 2ECh. 16.3 - Determine whether or not F is a conservative...Ch. 16.3 - Determine whether or not F is a conservative...Ch. 16.3 - Determine whether or not F is a conservative...Ch. 16.3 - Prob. 6ECh. 16.3 - Prob. 7ECh. 16.3 - Prob. 8ECh. 16.3 - Prob. 9ECh. 16.3 - Determine whether or not F is a conservative...Ch. 16.3 - The figure shows the vector field F(x,y)=2xy,x2...Ch. 16.3 - a Find a function f such that F=f and b use part a...Ch. 16.3 - a Find a function f such that F=f and b use part a...Ch. 16.3 - a Find a function f such that F=f and b use part a...Ch. 16.3 - a Find a function f such that F=f and b use part a...Ch. 16.3 - Prob. 16ECh. 16.3 - Prob. 17ECh. 16.3 - Prob. 18ECh. 16.3 - Show that the line integral is independent of path...Ch. 16.3 - Show that the line integral is independent of path...Ch. 16.3 - Suppose youre asked to determine the curve that...Ch. 16.3 - Prob. 22ECh. 16.3 - Find the work done by the force field F in moving...Ch. 16.3 - Find the work done by the force field F in moving...Ch. 16.3 - Is the vector field shown in the figure...Ch. 16.3 - Is the vector field shown in the figure...Ch. 16.3 - If F(x,y)=sinyi+(1+xcosy)j, use a plot to guess...Ch. 16.3 - Let F=f, where f(x,y)=sin(x2y). Find curves C1 and...Ch. 16.3 - Show that if the vector field F=Pi+Qj+Rk is...Ch. 16.3 - Use Exercise 29 to show that the line integral...Ch. 16.3 - Determine whether or not the given set is a open,...Ch. 16.3 - Determine whether or not the given set is a open,...Ch. 16.3 - Determine whether or not the given set is a open,...Ch. 16.3 - Prob. 34ECh. 16.3 - Prob. 35ECh. 16.3 - a Suppose that F is an inverse square force field,...Ch. 16.4 - Evaluate the line integral by two methods: a...Ch. 16.4 - Evaluate the line integral by two methods: a...Ch. 16.4 - Evaluate the line integral by two methods: a...Ch. 16.4 - Evaluate the line integral by two methods: a...Ch. 16.4 - Use Greens Theorem to evaluate the line integral...Ch. 16.4 - Use Greens Theorem to evaluate the line integral...Ch. 16.4 - Use Greens Theorem to evaluate the line integral...Ch. 16.4 - Use Greens Theorem to evaluate the line integral...Ch. 16.4 - Use Greens Theorem to evaluate the line integral...Ch. 16.4 - Use Greens Theorem to evaluate the line integral...Ch. 16.4 - Use Greens Theorem to evaluate cFdr. Check the...Ch. 16.4 - Prob. 12ECh. 16.4 - Prob. 13ECh. 16.4 - Prob. 14ECh. 16.4 - Verify Greens Theorem by using a computer algebra...Ch. 16.4 - Verify Greens Theorem by using a computer algebra...Ch. 16.4 - Prob. 17ECh. 16.4 - A particle starts at the origin, moves along the...Ch. 16.4 - Prob. 19ECh. 16.4 - If a circle C with radius 1 rolls along the...Ch. 16.4 - Prob. 21ECh. 16.4 - Prob. 22ECh. 16.4 - Use Exercise 22 to find the centroid of a...Ch. 16.4 - Prob. 24ECh. 16.4 - A plane lamina with constant density (x,y)=...Ch. 16.4 - Prob. 26ECh. 16.4 - Use the method of Example 5 to calculate CFdr,...Ch. 16.4 - Prob. 28ECh. 16.4 - If F is the vector field of Example 5, show that...Ch. 16.4 - Complete the proof of the special case of Greens...Ch. 16.4 - Prob. 31ECh. 16.5 - Find a the curl and b the divergence of the vector...Ch. 16.5 - Find a the curl and b the divergence of the vector...Ch. 16.5 - Find a the curl and b the divergence of the vector...Ch. 16.5 - Find a the curl and b the divergence of the vector...Ch. 16.5 - Find a the curl and b the divergence of the vector...Ch. 16.5 - Find a the curl and b the divergence of the vector...Ch. 16.5 - Find a the curl and b the divergence of the vector...Ch. 16.5 - Find a the curl and b the divergence of the vector...Ch. 16.5 - The vector field F is shown in the xy-plane and...Ch. 16.5 - The vector field F is shown in the xy-plane and...Ch. 16.5 - The vector field F is shown in the xy-plane and...Ch. 16.5 - Let f be a scalar field and F a vector field....Ch. 16.5 - Determine whether or not the vector field is...Ch. 16.5 - Determine whether or not the vector field is...Ch. 16.5 - Prob. 15ECh. 16.5 - Determine whether or not the vector field is...Ch. 16.5 - Prob. 17ECh. 16.5 - Determine whether or not the vector field is...Ch. 16.5 - Is there a vector field G on 3 such that curl...Ch. 16.5 - Prob. 20ECh. 16.5 - Show that any vector field of the form...Ch. 16.5 - Prob. 22ECh. 16.5 - Prob. 23ECh. 16.5 - Prove the identity, assuming that the appropriate...Ch. 16.5 - Prob. 25ECh. 16.5 - Prove the identity, assuming that the appropriate...Ch. 16.5 - Prob. 27ECh. 16.5 - Prove the identity, assuming that the appropriate...Ch. 16.5 - Prove the identity, assuming that the appropriate...Ch. 16.5 - Let r=xi+yj+zk and r=|r|. Verify each identity. a...Ch. 16.5 - Let r=xi+yj+zk and r=|r|. Verify each identity. a...Ch. 16.5 - Let r=xi+yj+zk and r=|r|. If F=r/rp, find div F....Ch. 16.5 - Use Greens Theorem in the form of Equation 13 to...Ch. 16.5 - Prob. 34ECh. 16.5 - Recall from Section 14.3 that a function g is...Ch. 16.5 - Prob. 36ECh. 16.5 - This exercise demonstrates a connection between...Ch. 16.5 - Maxwells equations relating the electric field E...Ch. 16.5 - We have seen that all vector fields of the form...Ch. 16.6 - Determine whether the points P and Q lie on the...Ch. 16.6 - Determine whether the points P and Q lie on the...Ch. 16.6 - Prob. 3ECh. 16.6 - Identify the surface with the given vector...Ch. 16.6 - Prob. 5ECh. 16.6 - Identify the surface with the given vector...Ch. 16.6 - Use a computer to graph the parametric surface....Ch. 16.6 - Prob. 8ECh. 16.6 - Prob. 9ECh. 16.6 - Prob. 10ECh. 16.6 - Prob. 11ECh. 16.6 - Prob. 12ECh. 16.6 - Match the equations with the graphs labeled IVI...Ch. 16.6 - Match the equations with the graphs labeled IVI...Ch. 16.6 - Match the equations with the graphs labeled IVI...Ch. 16.6 - Match the equations with the graphs labeled IVI...Ch. 16.6 - Prob. 17ECh. 16.6 - Prob. 18ECh. 16.6 - Find da parametric representation for the surface....Ch. 16.6 - Find da parametric representation for the surface....Ch. 16.6 - Find da parametric representation for the surface....Ch. 16.6 - Find da parametric representation for the surface....Ch. 16.6 - Find da parametric representation for the surface....Ch. 16.6 - Find da parametric representation for the surface....Ch. 16.6 - Find da parametric representation for the surface....Ch. 16.6 - Find da parametric representation for the surface....Ch. 16.6 - Prob. 27ECh. 16.6 - Prob. 28ECh. 16.6 - Prob. 29ECh. 16.6 - Prob. 30ECh. 16.6 - a What happens to the spiral tube in Example 2 see...Ch. 16.6 - Prob. 32ECh. 16.6 - Find an equation of the tangent plane to the given...Ch. 16.6 - Find an equation of the tangent plane to the given...Ch. 16.6 - Prob. 35ECh. 16.6 - Prob. 36ECh. 16.6 - Prob. 37ECh. 16.6 - Prob. 38ECh. 16.6 - Prob. 39ECh. 16.6 - Prob. 40ECh. 16.6 - Find the area of the surface. The part of the...Ch. 16.6 - Find the area of the surface. The part of the cone...Ch. 16.6 - Find the area of the surface. The surface...Ch. 16.6 - Find the area of the surface. The part of the...Ch. 16.6 - Find the area of the surface. The part of the...Ch. 16.6 - Find the area of the surface. The part of the...Ch. 16.6 - Find the area of the surface. The part of the...Ch. 16.6 - Prob. 48ECh. 16.6 - Find the area of the surface. The surface with...Ch. 16.6 - Find the area of the surface. The part of the...Ch. 16.6 - Prob. 51ECh. 16.6 - Prob. 52ECh. 16.6 - Prob. 53ECh. 16.6 - Prob. 54ECh. 16.6 - Prob. 55ECh. 16.6 - Prob. 56ECh. 16.6 - Prob. 57ECh. 16.6 - Prob. 58ECh. 16.6 - a Show that the parametric equations...Ch. 16.6 - a Show that the parametric equations...Ch. 16.6 - Find the area of the part of the sphere...Ch. 16.6 - The figure shows the surface created when the...Ch. 16.6 - Prob. 63ECh. 16.6 - a Find a parametric representation for the torus...Ch. 16.7 - Let S be the surface of the box enclosed by the...Ch. 16.7 - Prob. 2ECh. 16.7 - Prob. 3ECh. 16.7 - Suppose that f(x,y,z)=g(x2+y2+z2), where g is a...Ch. 16.7 - Evaluate the surface integral. S(x+y+z)dS, S is...Ch. 16.7 - Evaluate the surface integral. SxyzdS, S is the...Ch. 16.7 - Prob. 7ECh. 16.7 - Evaluate the surface integral. S(x2+y2)dS, S is...Ch. 16.7 - Evaluate the surface integral. Sx2yzdS, S is the...Ch. 16.7 - Prob. 10ECh. 16.7 - Evaluate the surface integral. SxdS, S is the...Ch. 16.7 - Evaluate the surface integral. SydS, S is the...Ch. 16.7 - Evaluate the surface integral. Sz2dS, S is the...Ch. 16.7 - Evaluate the surface integral. Sy2z2dS, S is the...Ch. 16.7 - Prob. 15ECh. 16.7 - Evaluate the surface integral. Sy2dS, S is the...Ch. 16.7 - Prob. 17ECh. 16.7 - Evaluate the surface integral. S(x+y+z)dS, S is...Ch. 16.7 - Evaluate the surface integral. SxzdS, S is the...Ch. 16.7 - Prob. 20ECh. 16.7 - Evaluate the surface integral SFdS for the given...Ch. 16.7 - Evaluate the surface integral SFdS for the given...Ch. 16.7 - Evaluate the surface integral SFdS for the given...Ch. 16.7 - Evaluate the surface integral SFdS for the given...Ch. 16.7 - Evaluate the surface integral SFdS for the given...Ch. 16.7 - Evaluate the surface integral SFdS for the given...Ch. 16.7 - Evaluate the surface integral SFdS for the given...Ch. 16.7 - Evaluate the surface integral SFdS for the given...Ch. 16.7 - Evaluate the surface integral SFdS for the given...Ch. 16.7 - Evaluate the surface integral SFdS for the given...Ch. 16.7 - Evaluate the surface integral SFdS for the given...Ch. 16.7 - Evaluate the surface integral SFdS for the given...Ch. 16.7 - Prob. 33ECh. 16.7 - Prob. 34ECh. 16.7 - Prob. 35ECh. 16.7 - Find the flux of F(x,y,z)=sin(xyz)i+x2yj+z2ex/5k...Ch. 16.7 - Prob. 37ECh. 16.7 - Prob. 38ECh. 16.7 - Find the centre of mass of the hemisphere...Ch. 16.7 - Find the mass of a thin funnel in the shape of a...Ch. 16.7 - Prob. 41ECh. 16.7 - Let S be the part of the sphere x2+y2+z2=25 that...Ch. 16.7 - Prob. 43ECh. 16.7 - Prob. 44ECh. 16.7 - Use Gausss Law to find the charge contained in the...Ch. 16.7 - Prob. 46ECh. 16.7 - Prob. 47ECh. 16.7 - Prob. 48ECh. 16.7 - Prob. 49ECh. 16.8 - A hemisphere H and a portion P of a paraboloid are...Ch. 16.8 - Use Stokes Theorem to evaluate ScurlFdS...Ch. 16.8 - Use Stokes Theorem to evaluate ScurlFdS....Ch. 16.8 - Use Stokes Theorem to evaluate ScurlFdS....Ch. 16.8 - Use Stokes Theorem to evaluate ScurlFdS....Ch. 16.8 - Use Stokes Theorem to evaluate ScurlFdS...Ch. 16.8 - Use Stokes Theorem to evaluate cFdr. In each case...Ch. 16.8 - Prob. 8ECh. 16.8 - Use Stokes Theorem to evaluate cFdr. In each case...Ch. 16.8 - Use Stokes Theorem to evaluate cFdr. In each case...Ch. 16.8 - a Use Stokes Theorem to evaluate cFdr, where...Ch. 16.8 - a Use Stokes Theorem to evaluate cFdr, where...Ch. 16.8 - Verify the Stokes Theorem is true for the given...Ch. 16.8 - Verify that Stokes Theorem is true for given...Ch. 16.8 - Verify that Stokes Theorem is true for given...Ch. 16.8 - Let C be a simple closed smooth curve that lies in...Ch. 16.8 - A particle moves along line segments from the...Ch. 16.8 - Evaluate C(y+sinx)dx+(z2+cosy)dy+x3dz where C is...Ch. 16.8 - Prob. 19ECh. 16.8 - Suppose S and C satisfy the hypotheses of Stokes...Ch. 16.9 - Verify that the Divergence Theorem is true for the...Ch. 16.9 - Verify that the Divergence Theorem is true for the...Ch. 16.9 - Prob. 3ECh. 16.9 - Prob. 4ECh. 16.9 - Prob. 5ECh. 16.9 - Use the Divergence Theorem to calculate the...Ch. 16.9 - Prob. 7ECh. 16.9 - Prob. 8ECh. 16.9 - Prob. 9ECh. 16.9 - Use the Divergence Theorem to calculate the...Ch. 16.9 - Use the Divergence Theorem to calculate the...Ch. 16.9 - Use the Divergence Theorem to calculate the...Ch. 16.9 - Use the Divergence Theorem to calculate the...Ch. 16.9 - Prob. 14ECh. 16.9 - Use the Divergence Theorem to calculate the...Ch. 16.9 - Use a computer algebra system to plot the vector...Ch. 16.9 - Use a Divergence Theorem to evaluate SFdS, where...Ch. 16.9 - Let F(x,y,z)=ztan1(y2)i+z3ln(x2+1)j+zk. Find the...Ch. 16.9 - A vector field F is shown. Use the interpretation...Ch. 16.9 - a Are the points P1 and P2 sources or sinks for...Ch. 16.9 - Prob. 21ECh. 16.9 - Prob. 22ECh. 16.9 - Verify that div E=0 for the electric field...Ch. 16.9 - Prob. 24ECh. 16.9 - Prob. 25ECh. 16.9 - Prove each identity, assuming that S and E satisfy...Ch. 16.9 - Prove each identity, assuming that S and E satisfy...Ch. 16.9 - Prove each identity, assuming that S and E satisfy...Ch. 16.9 - Prove each identity, assuming that S and E satisfy...Ch. 16.9 - Prob. 30ECh. 16.9 - Suppose S and E satisfy the conditions of the...Ch. 16.9 - Prob. 32ECh. 16.R - Prob. 1CCCh. 16.R - a What is a conservative vector field? b What is...Ch. 16.R - Prob. 3CCCh. 16.R - a Define the line integral of a vector field F...Ch. 16.R - Prob. 5CCCh. 16.R - Prob. 6CCCh. 16.R - Prob. 7CCCh. 16.R - Write expressions for the area enclosed by a curve...Ch. 16.R - Prob. 9CCCh. 16.R - Prob. 10CCCh. 16.R - Prob. 11CCCh. 16.R - Prob. 12CCCh. 16.R - Prob. 13CCCh. 16.R - Prob. 14CCCh. 16.R - Prob. 15CCCh. 16.R - Prob. 16CCCh. 16.R - Prob. 1TFQCh. 16.R - Prob. 2TFQCh. 16.R - Prob. 3TFQCh. 16.R - Prob. 4TFQCh. 16.R - Prob. 5TFQCh. 16.R - Prob. 6TFQCh. 16.R - Prob. 7TFQCh. 16.R - Prob. 8TFQCh. 16.R - Prob. 9TFQCh. 16.R - Prob. 10TFQCh. 16.R - Prob. 11TFQCh. 16.R - Prob. 12TFQCh. 16.R - Prob. 13TFQCh. 16.R - A vector field F, a curve C, and a point P are...Ch. 16.R - Evaluate the line integral. cxds, C is the arc of...Ch. 16.R - Evaluate the line integral. cyzcosxds,...Ch. 16.R - Evaluate the line integral. cydx+(x+y2)dy, C is...Ch. 16.R - Prob. 5ECh. 16.R - Evaluate the line integral. cxydx+eydy+xzdz, C is...Ch. 16.R - Prob. 7ECh. 16.R - Evaluate the line integral. cFdr, where...Ch. 16.R - Prob. 9ECh. 16.R - Find the work done by the force field...Ch. 16.R - Show that F is a conservative vector field. Then...Ch. 16.R - Prob. 12ECh. 16.R - Prob. 13ECh. 16.R - Show that F is a conservative and use this fact to...Ch. 16.R - Verify that Greens Theorem is true for the line...Ch. 16.R - Prob. 16ECh. 16.R - Use Greens theorem to evaluate cx2ydxxy2dy, where...Ch. 16.R - Prob. 18ECh. 16.R - Show that there is no vector field G such that...Ch. 16.R - Prob. 20ECh. 16.R - Prob. 21ECh. 16.R - If f and g are twice differentiable functions,...Ch. 16.R - If f is a harmonic function, that is, 2f=0, show...Ch. 16.R - a Sketch the curve C with parametric equations...Ch. 16.R - Prob. 25ECh. 16.R - Prob. 26ECh. 16.R - Prob. 27ECh. 16.R - Prob. 28ECh. 16.R - Evaluate the surface integral. sFdS, where...Ch. 16.R - Prob. 30ECh. 16.R - Verify that Stokes Theorem is true for the vector...Ch. 16.R - Prob. 32ECh. 16.R - Use Stokes Theorem to evaluate cFdr, where...Ch. 16.R - Use the Divergence Theorem to calculate the...Ch. 16.R - Prob. 35ECh. 16.R - Compute the outward flux of...Ch. 16.R - Prob. 37ECh. 16.R - Let F(x,y)=(2x3+2xy22y)i+(2y3+2x2y+2x)jx2+y2...Ch. 16.R - Find sFndS, where F(x,y,z)=xi+yj+zk and S is the...Ch. 16.R - Prob. 40ECh. 16.R - Prob. 41ECh. 16.P - Let S be a smooth parametric surface and P be a...Ch. 16.P - Find the positively oriented simple closed curve C...Ch. 16.P - Let C be a simple closed piecewise-smooth space...Ch. 16.P - Investigate the shape of the surface with...Ch. 16.P - Prove the following identity:...Ch. 16.P - The depicts the sequence of events in each...
Knowledge Booster
Background pattern image
Calculus
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.
Similar questions
SEE MORE QUESTIONS
Recommended textbooks for you
Text book image
Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning
Text book image
Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON
Text book image
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON
Text book image
Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman
Text book image
Precalculus
Calculus
ISBN:9780135189405
Author:Michael Sullivan
Publisher:PEARSON
Text book image
Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning
SEE MORE TEXTBOOKS
Basic Differentiation Rules For Derivatives; Author: The Organic Chemistry Tutor;https://www.youtube.com/watch?v=IvLpN1G1Ncg;License: Standard YouTube License, CC-BY