Chapter 16, Problem 54E

The two-port of Fig. 16.65 can be viewed as three separate cascaded two-ports A, B, and C. (a) Compute t for each network. (b) Obtain t for the cascaded network. (c) Verify your answer by naming the two middle nodes V_x and V_y, respectively, writing nodal equations, obtaining the admittance parameters from your nodal equations, and converting to t parameters using Table 16.1.

To determine

The $t$ parameter for each network.

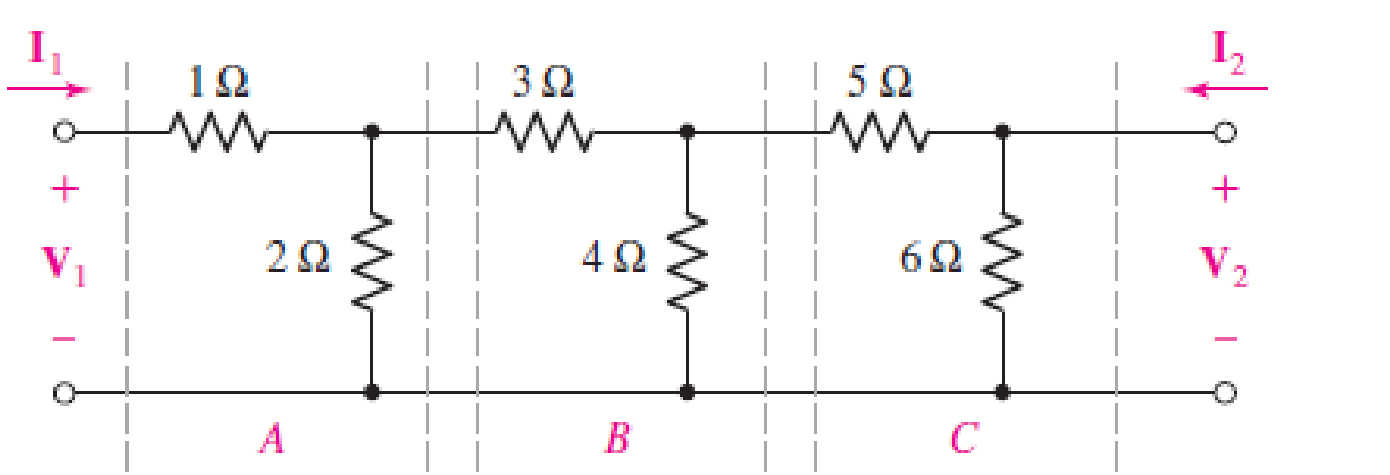
Answer to Problem 54E

The $t$ parameters of network $A$, $B$ and $C$ are $\left[\begin{array}{cc}1.5& 1\Omega \\ 0.5\text{S}& 1\end{array}\right]$, $\left[\begin{array}{cc}1.75& 3\Omega \\ 0.25\text{S}& 1\end{array}\right]$ and $\left[\begin{array}{cc}1.83& 5\Omega \\ 0.167\text{S}& 1\end{array}\right]$ respectively.

Explanation of Solution

Calculation:

The required diagram is shown in Figure 1.

Here,

$I_1$ is the current from input node.

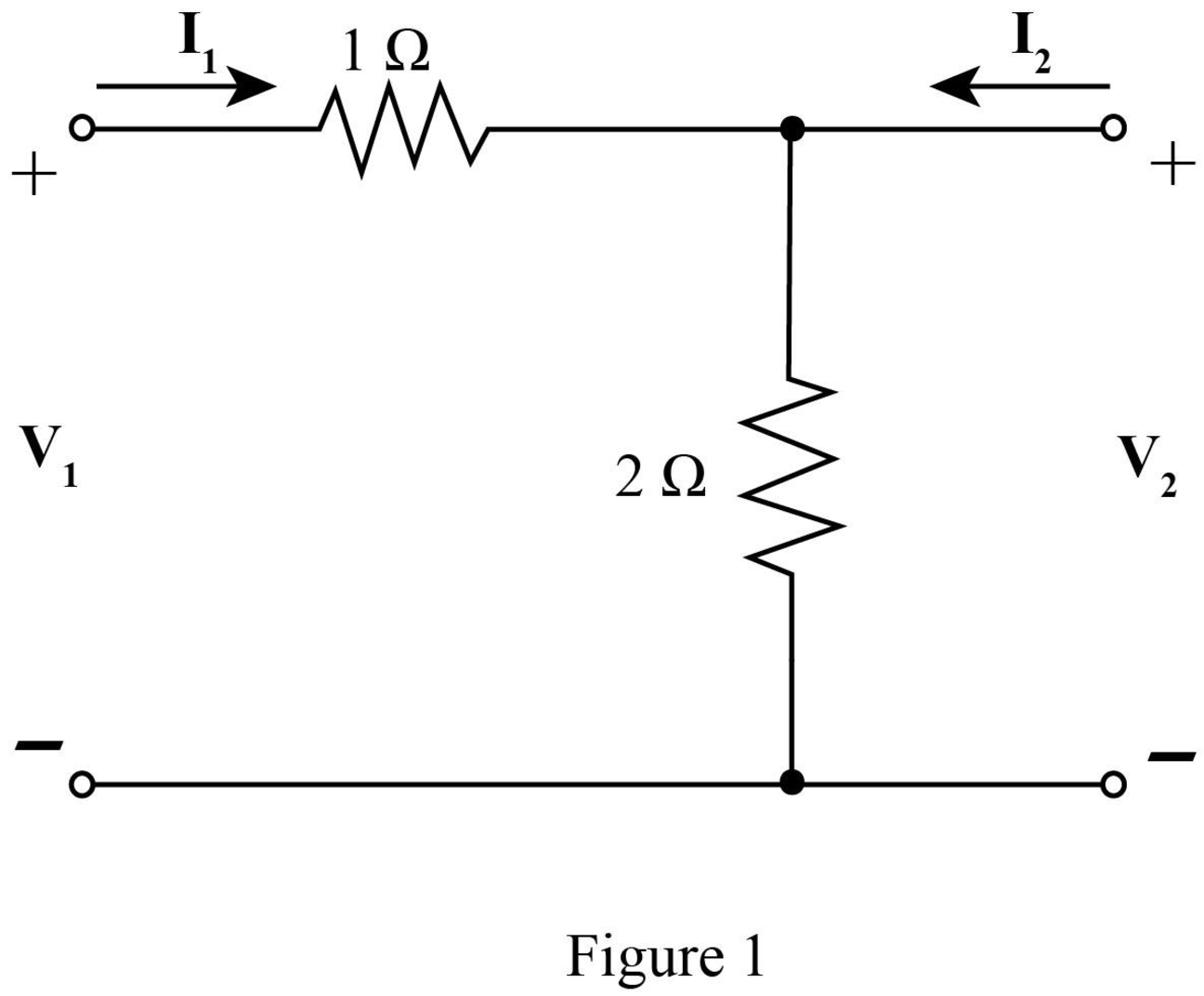
$I_2$ is the current from output node.

The mesh equation from the input side is given by,

$\begin{array}{c}{V}_1=\left(1\right)\left(I_1\right)+\left(2\right)\left(I_1+I_2\right)\\ =I_1+2I_1+2I_2\\ =3I_1+2I_2\end{array}$        (1)

The mesh equations at the output side is given by,

$\begin{array}{l}{V}_2=2\left(I_1+I_2\right)\\ V_2=2I_1+2I_2\\ 2I_1=V_2-2I_2\\ I_1=0.5V_2-I_2\end{array}$        (2)

Substitute $0.5V_2-I_2$ for $I_1$  in equation (1).

$\begin{array}{c}{V}_1=3\left(0.5V_2-I_2\right)+2I_2\\ =1.5V_2-3I_2+2I_2\\ =1.5V_2-I_2\end{array}$        (3)

The $t$ parameters of a two port network are given by,

$V_1=t_{11}{V}_2-t_{12}{I}_2$        (4)

$I_1=t_{21}{V}_2-t_{22}{I}_2$        (5)

Here,

$t_{11}$ is the open circuit voltage gain.

$t_{12}$ is the short circuit impedance.

$t_{21}$ is the open circuit admittance.

$t_{22}$ is the short circuit current gain.

Write equations (6) and (7) in matrix form.

$\left[\begin{array}{c}{V}_1\\ I_1\end{array}\right]=\left[\begin{array}{cc}{t}_{11}& t_{12}\\ t_{21}& t_{22}\end{array}\right]\left[\begin{array}{c}{V}_2\\ -I_2\end{array}\right]$

Compare equation (3) with equation (4).

$\begin{array}{c}{t}_{11}=1.5\\ t_{12}=1\Omega \end{array}$

Compare equation (2) with equation (6).

$\begin{array}{c}{t}_{21}=0.5\text{S}\\ t_{22}=1\end{array}$

The $t$ parameter of network $A$ $t_A$ is given by,

$\left[\begin{array}{cc}1.5& 1\Omega \\ 0.5\text{S}& 1\end{array}\right]$

The required diagram is shown in Figure 2.

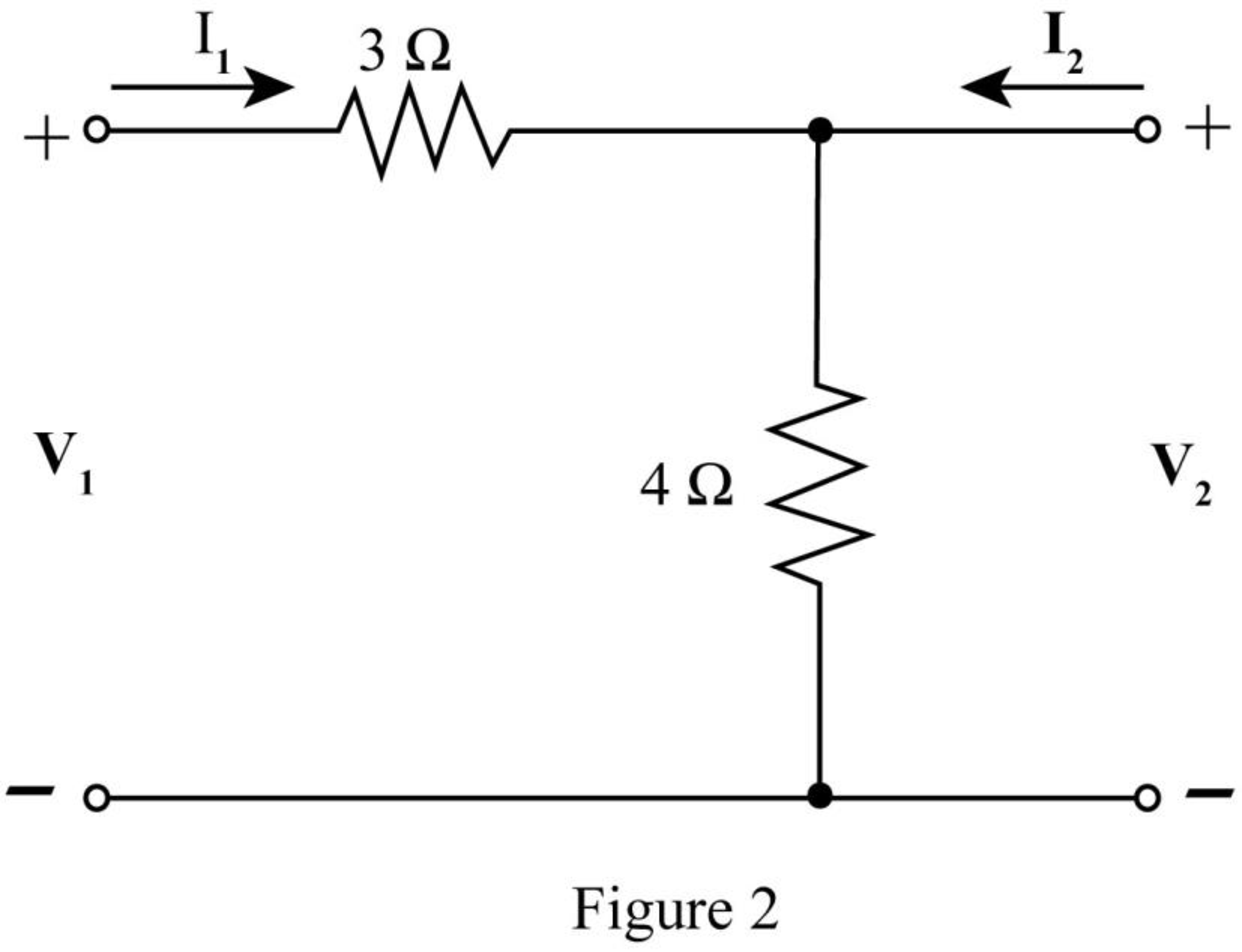
The mesh equation from the input side is given by,

$\begin{array}{c}{V}_1=\left(3\right)\left(I_1\right)+\left(4\right)\left(I_1+I_2\right)\\ =3I_1+4I_1+4I_2\\ =7I_1+4I_2\end{array}$        (6)

The mesh equations at the output side is given by,

$\begin{array}{l}{V}_2=4\left(I_1+I_2\right)\\ V_2=4I_1+4I_2\\ 4I_1=V_2-4I_2\\ I_1=0.25V_2-I_2\end{array}$        (7)

Substitute $0.25V_2-I_2$ for $I_1$ in equation (6).

$\begin{array}{c}{V}_1=7\left(0.25V_2-I_2\right)+4I_2\\ =1.75V_2-7I_2+4I_2\\ =1.75V_2-3I_2\end{array}$        (8)

Compare equation (8) with equation (4).

$\begin{array}{c}{t}_{11}=1.75\\ t_{12}=3\Omega \end{array}$

Compare equation (7) with equation (5).

$\begin{array}{c}{t}_{21}=0.25\text{S}\\ t_{22}=1\end{array}$

The $t$ parameter of network $B$ $t_B$ is given by,

$\left[\begin{array}{cc}1.75& 3\Omega \\ 0.25\text{S}& 1\end{array}\right]$

The required diagram is shown in Figure 3.

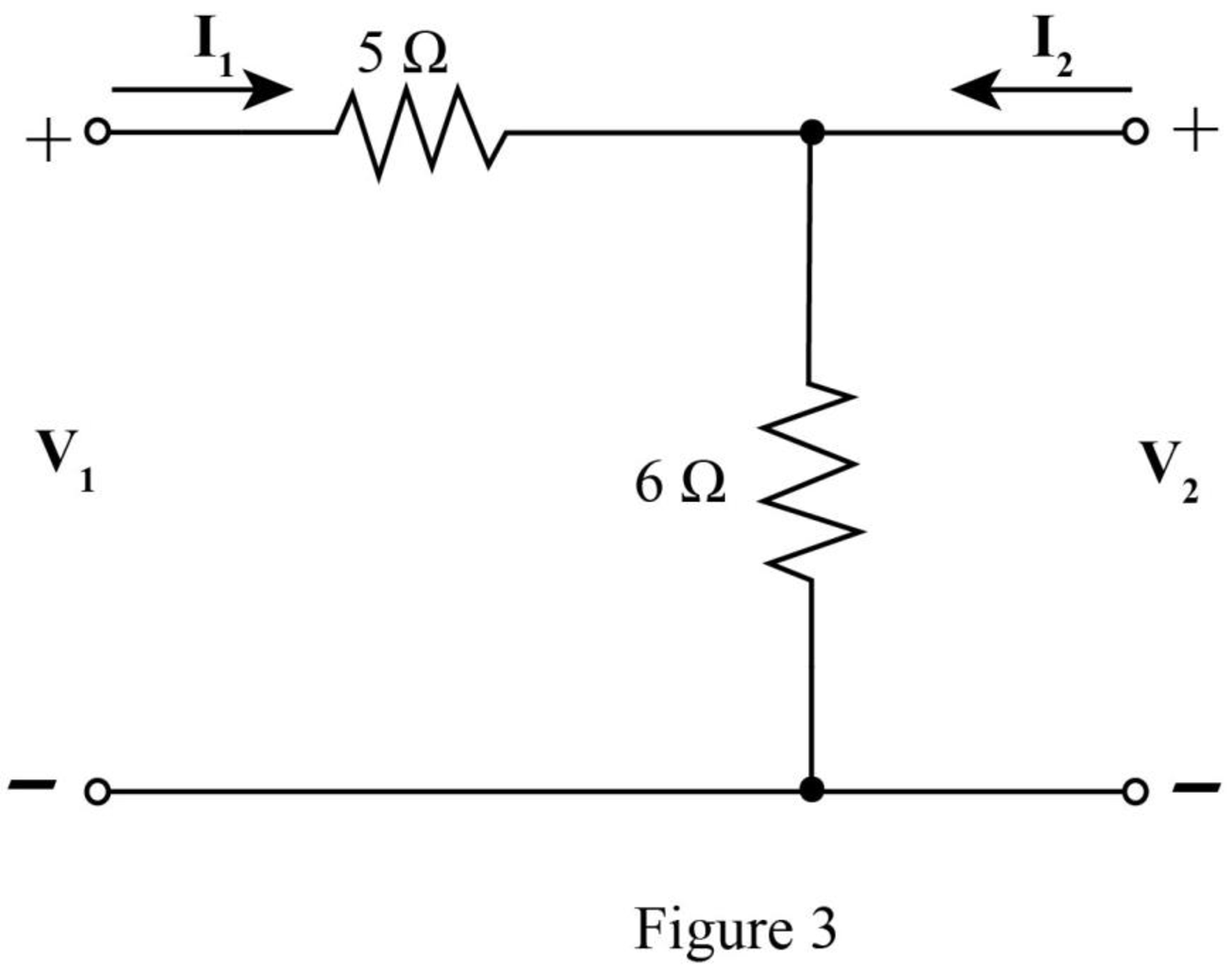
The mesh equation from the input side is given by,

$\begin{array}{c}{V}_1=\left(5\right)\left(I_1\right)+\left(6\right)\left(I_1+I_2\right)\\ =5I_1+6I_1+6I_2\\ =11I_1+6I_2\end{array}$        (9)

The mesh equations at the output side is given by,

$\begin{array}{l}{V}_2=6\left(I_1+I_2\right)\\ V_2=6I_1+6I_2\\ 6I_1=V_2-6I_2\\ I_1=0.167V_2-I_2\end{array}$        (10)

Substitute $0.167V_2-I_2$ for $I_1$ in equation (9).

$\begin{array}{c}{V}_1=11\left(0.167V_2-I_2\right)+6I_2\\ =1.83V_2-11I_2+6I_2\\ =1.83V_2-5I_2\end{array}$        (11)

Compare equation (11) with equation (4).

$\begin{array}{c}{t}_{11}=1.83\\ t_{12}=5\Omega \end{array}$

Compare equation (10) with equation (5).

$\begin{array}{c}{t}_{21}=0.167\text{S}\\ t_{22}=1\end{array}$

The $t$ parameter of network $C$ $t_C$ is given by,

$\left[\begin{array}{cc}1.83& 5\Omega \\ 0.167\text{S}& 1\end{array}\right]$

Conclusion:

Therefore, the $t$ parameters of network $A$, $B$ and $C$ are $\left[\begin{array}{cc}1.5& 1\Omega \\ 0.5\text{S}& 1\end{array}\right]$, $\left[\begin{array}{cc}1.75& 3\Omega \\ 0.25\text{S}& 1\end{array}\right]$ and $\left[\begin{array}{cc}1.83& 5\Omega \\ 0.167\text{S}& 1\end{array}\right]$ respectively.

To determine

The $t$ parameter for cascaded network.

Answer to Problem 54E

The $t$ parameter for the cascaded network is $\left[\begin{array}{cc}6.18& 19.8\Omega \\ 2.47\text{S}& 8.12\end{array}\right]$.

Explanation of Solution

Calculation:

The $t$ parameter for the cascaded network $t_n$ is given by,

$t_{\text{n}}=t_A{t}_B{t}_C$

Substitute $\left[\begin{array}{cc}1.5& 1\Omega \\ 0.5\text{S}& 1\end{array}\right]$ for $t_A$, $\left[\begin{array}{cc}1.75& 3\Omega \\ 0.25\text{S}& 1\end{array}\right]$ for $t_B$ and $\left[\begin{array}{cc}1.83& 5\Omega \\ 0.167\text{S}& 1\end{array}\right]$ for $t_C$ in the above equation.

$\begin{array}{c}{t}_{\text{n}}=\left[\begin{array}{cc}1.5& 1\Omega \\ 0.5\text{S}& 1\end{array}\right]·\left[\begin{array}{cc}1.75& 3\Omega \\ 0.25\text{S}& 1\end{array}\right]·\left[\begin{array}{cc}1.83& 5\Omega \\ 0.167\text{S}& 1\end{array}\right]\\ =\left[\begin{array}{cc}2.875& 5.5\Omega \\ 1.125\text{S}& 2.5\end{array}\right]·\left[\begin{array}{cc}1.83& 5\Omega \\ 0.167\text{S}& 1\end{array}\right]\\ =\left[\begin{array}{cc}6.18& 19.8\Omega \\ 2.47\text{S}& 8.12\end{array}\right]\end{array}$

Conclusion:

Therefore, the $t$ parameter for the cascaded network is $\left[\begin{array}{cc}6.18& 19.8\Omega \\ 2.47\text{S}& 8.12\end{array}\right]$.

To determine

To verify: The above answers by obtaining the admittance parameter and converting them to $t$ parameter.

Answer to Problem 54E

The values have been verified.

Explanation of Solution

Calculation:

The required diagram is shown in Figure 4.

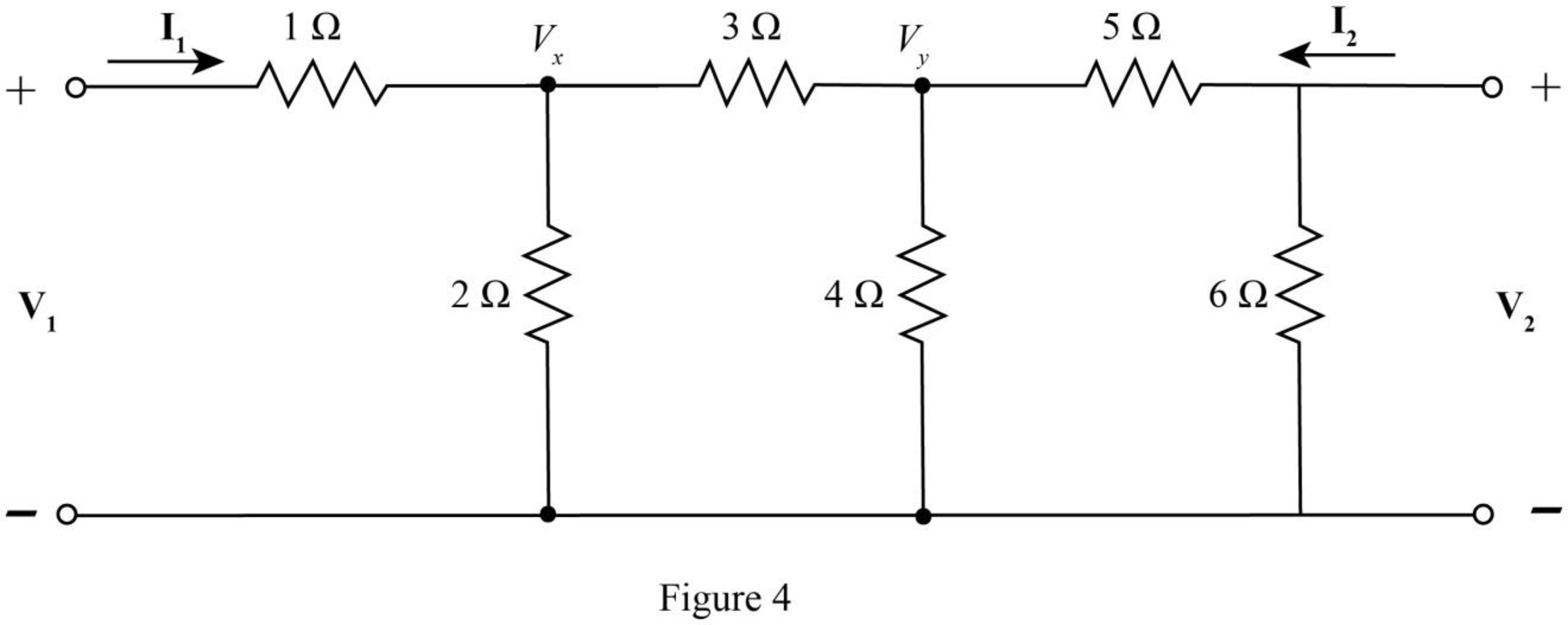
The nodal equation at node $V_x$ is given by,

$\begin{array}{l}\frac{V_x-V_1}{1}+\frac{V_x}{2}+\frac{V_x-V_y}{3}=0\\ V_x-V_1+0.5V_x+0.333V_x-0.333V_y=0\\ 1.833V_x-V_1-0.333V_y=0\\ V_y=5.504V_x-3V_1\end{array}$        (12)

The nodal equations at node $V_y$ is given by,

$\begin{array}{l}\frac{V_y-V_x}{3}+\frac{V_y}{4}+\frac{V_y-V_2}{5}=0\\ 0.333V_y-0.333V_x+10.25V_y+0.2V_y-0.2V_2=0\\ 0.783V_y-0.333V_x-0.2V_2=0\\ V_x=2.351V_y-0.6V_2\end{array}$        (13)

Substitute $2.351V_y-0.6V_2$ for $V_x$ in equation (12).

$\begin{array}{l}{V}_y=5.504\left(2.351V_y-0.6V_2\right)-3V_1\\ =12.941V_y-3.306V_2-3V_1\\ 11.941V_y=3.306V_2+3V_1\\ V_y=0.28V_2+0.25V_1\end{array}$        (14)

Substitute $0.28V_2+0.25V_1$ for $V_y$ in equation (13).

$\begin{array}{c}{V}_x=2.351\left(0.28V_2+0.25V_1\right)-0.6V_2\\ =0.65V_2+0.59V_1-0.6V_2\\ =0.59V_1+0.05V_2\end{array}$        (15)

The current $I_1$ is given by,

$\begin{array}{c}{I}_1=\frac{V_1-V_x}{1}\\ =V_1-V_x\end{array}$

Substitute $0.59V_1+0.05V_2$ for $V_x$ in the above equation.

$\begin{array}{c}{I}_1=V_1-\left(0.59V_1+0.05V_2\right)\\ =0.41V_1-0.05V_2\end{array}$        (16)

The current $I_2$ is given by,

$\begin{array}{c}{I}_2=\frac{V_2}{6}+\frac{V_2-V_y}{5}\\ =0.166V_2+0.2V_2-0.2V_y\\ =0.366V_2-0.2V_y\end{array}$

Substitute $0.28V_2+0.25V_1$ for $V_y$ in the above equation.

$\begin{array}{c}{I}_2=0.366V_2-0.2\left(0.28V_2+0.25V_1\right)\\ =-0.05V_1+0.31V_2\end{array}$        (17)

The $y$ parameters of a two port network are given by,

$I_1=y_{11}{V}_1+y_{12}{V}_2$        (18)

$I_2=y_{21}{V}_1+y_{22}{V}_2$        (19)

Here,

$y_{11}$ is the short circuit input admittance.

$y_{12}$ is the short circuit transfer admittance.

$y_{21}$ is the short circuit transfer admittance.

$y_{22}$ is the short circuit output admittance.

Compare equation (16) with equation (18).

$\begin{array}{l}{y}_{11}=0.41\text{S}\\ y_{12}=-0.05\text{S}\end{array}$

Compare equation (17) with equation (19).

$\begin{array}{l}{y}_{21}=-0.05\text{S}\\ y_{22}=0.31\text{S}\end{array}$

The determinant of the matrix ${\Delta }_y$ is given by,

${\Delta }_y=\left(y_{11}\right)\left(y_{22}\right)-\left(y_{21}\right)\left(y_{12}\right)$

Substitute $0.41\text{S}$ for $y_{11}$ , $-0.05\text{S}$ for $y_{12}$ , $-0.05\text{S}$ for $y_{21}$ and $0.31\text{S}$ for $y_{22}$ in the above equation.

$\begin{array}{c}{\Delta }_y=\left(0.41\text{S}\right)\left(0.31\text{S}\right)-\left(-0.05\text{S}\right)\left(-0.05\text{S}\right)\\ =\left(0.1271-0.00025\right){\text{S}}^2\\ =0.125{\text{S}}^{\text{2}}\end{array}$

The relation between $t$ and $y$ parameters is given by,

$t=\left[\begin{array}{cc}\frac{-y_{22}}{y_{21}}& \frac{-1}{y_{21}}\\ \frac{-{\Delta }_{\text{y}}}{y_{21}}& \frac{-y_{11}}{y_{21}}\end{array}\right]$

Substitute $0.41\text{S}$ for $y_{11}$ , $-0.05\text{S}$ for $y_{12}$ , $-0.05\text{S}$ for $y_{21}$, $0.31\text{S}$ for $y_{22}$ and $0.125{\text{S}}^{\text{2}}$ for ${\Delta }_{\text{y}}$ in the above equation.

$\begin{array}{c}t=\left[\begin{array}{cc}\frac{-0.31\text{S}}{-0.05\text{S}}& \frac{-1}{-0.05\text{S}}\\ \frac{-0.125{\text{S}}^2}{-0.05\text{S}}& \frac{-0.41\text{S}}{-0.05\text{S}}\end{array}\right]\\ =\left[\begin{array}{cc}6.2& 20\Omega \\ 2.5\text{S}& 8.2\end{array}\right]\end{array}$

Within the limits of error, the values have been verified.

Conclusion:

Therefore, the values have been verified.