EBK NUMERICAL METHODS FOR ENGINEERS
7th Edition
ISBN: 8220100254147
Author: Chapra
Publisher: MCG
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 16, Problem 4P
The specific growth rate of a yeast that produces an antibiotic is a function of the food concentration c,
As depicted in Fig. P16.4, growth goes to zero at very low concentrations due to food limitation. It also goes to zero at high concentrations due to toxicity effects. Find the value of c at which growth is a maximum.
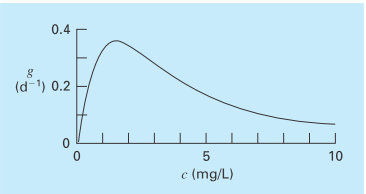
FIGURE P16.4
The specific growth rate of a yeast that produces an antibiotic versus the food concentration.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Chapter 16 Solutions
EBK NUMERICAL METHODS FOR ENGINEERS
Ch. 16 - 16.1 Design the optimal cylindrical container...Ch. 16 - 16.2 (a) Design the optimal conical container...Ch. 16 - Design the optimal cylindrical tank with...Ch. 16 - The specific growth rate of a yeast that produces...Ch. 16 - A chemical plant makes three major products on a...Ch. 16 - 16.6 Recently chemical engineers have become...Ch. 16 - 16.7 A mixture of benzene and toluene are to be...Ch. 16 - 16.8 A compound A will be converted into B in a...Ch. 16 - In problem 16.8, only one reactor is used. If two...Ch. 16 - 16.10 For the reaction:
equilibrium can be...
Ch. 16 - A chemical plant requires 106L/day of a solution....Ch. 16 - You must design a triangular open channel to carry...Ch. 16 - 16.13 As an agricultural engineer, you must design...Ch. 16 - 16.14 Find the optimal dimensions for a heated...Ch. 16 - A finite-element model of a cantilever beam...Ch. 16 - 16.16 Suppose that you are asked to design a...Ch. 16 - TheStreeter-Phelps model can be used to compute...Ch. 16 - Prob. 18PCh. 16 - 16.19 The flow in an open channel can be predicted...Ch. 16 - A cylindrical beam carries a compression load...Ch. 16 - The Splash River has a flow rate of 2106m3/d, of...Ch. 16 - 16.22 Determine the beam cross-sectional areas...Ch. 16 - AtotalchargeQ is uniformly distributed around a...Ch. 16 - A system consist softwopower plants that must...Ch. 16 - 16.25 The torque transmitted to an induction motor...Ch. 16 - (a) A computer equipment manufacture rproduces...Ch. 16 - A manufacturer provides specialized microchips....Ch. 16 - 16.28 The total drag on an airfoil can be...Ch. 16 - Mechanical/Aerospace Engineering
16.29 Roller...Ch. 16 - 16.30 An aerospace company is developing a new...Ch. 16 - 16.31 A manufacturing firm produces four types of...Ch. 16 - In a similar fashion to the case study described...Ch. 16 - 16.33 Recent interest in competitive and...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Similar questions
- The table shows the mid-year populations (in millions) of five countries in 2015 and the projected populations (in millions) for the year 2025. (a) Find the exponential growth or decay model y=aebt or y=aebt for the population of each country by letting t=15 correspond to 2015. Use the model to predict the population of each country in 2035. (b) You can see that the populations of the United States and the United Kingdom are growing at different rates. What constant in the equation y=aebt gives the growth rate? Discuss the relationship between the different growth rates and the magnitude of the constant.arrow_forwardTable 6 shows the population, in thousands, of harbor seals in the Wadden Sea over the years 1997 to 2012. a. Let x represent time in years starting with x=0 for the year 1997. Let y represent the number of seals in thousands. Use logistic regression to fit a model to these data. b. Use the model to predict the seal population for the year 2020. c. To the nearest whole number, what is the limiting value of this model?arrow_forwardThe population P (in millions) of Texas from 2001 through 2014 can be approximated by the model P=20.913e0.0184t, where t represents the year, with t=1 corresponding to 2001. According to this model, when will the population reach 32 million?arrow_forward
- bThe average rate of change of the linear function f(x)=3x+5 between any two points is ________.arrow_forwardFocal Length A refracting telescope has a main lens, or objective lens, and a second lens, the eyepiece see Figure 3.42. For a given magnification M of the telescope, the focal length F of the objective lens is a linear function of the focal length Fe of the eyepiece. For example, a telescope with magnification M=80 times can be constructed using various combinations of lenses. The following table gives some samples of focal length for telescopes with magnification M=80. Here focal lengths are in centimeters. Fe 0.3 0.5 0.7 0.9 F 24 40 56 72 a. Construct a linear model for the data. b. In this example, the magnification M is 80. In general, F is proportional to Fe, and the constant of proportionality is M. Use this relation to write a formula for F in terms of Fe and M. c. Solve the equation you obtained in part b for M and thus obtain a formula for magnification as a function of objective lens focal length and eyepiece focal length. d. To achieve a large magnification, how should the objective and eyepiece lenses be selected? FIGURE 3.42arrow_forwardEastern Pacific Yellowfin Tuna Studies to fit a logistic model to the Eastern Pacific yellowfin tuna population have yielded N=1481+36e2.61t where t is measured in years and N is measured in thousands of tons of fish. a. What is the r value for the Eastern Pacific yellowfin tuna? b. What is the carrying capacity K for the Eastern Pacific yellowfin tuna? c. What is the optimum yield level? d. Use your calculator to graph N versus t. e. At what time was the population growing the most rapidly?arrow_forward
- When a certain drug is taken orally, the concentration of the drug in the patient's bloodstream After t minutes is given by C(t)=0.06t0.0002t2 where 0t240 and concentration is measured in mg/L .When is the maximum serum concentration reached, and what is that maximum concentration?arrow_forwardWorld Population The following table shows world population N, in billions, in the given year. Year 1950 1960 1970 1980 1990 2000 2010 N 2.56 3.04 3.71 4.45 5.29 6.09 6.85 a. Use regression to find a logistic model for world population. b. What r value do these data yield for humans on planet Earth? c. According to the logistic model using these data, what is the carrying capacity of planet Earth for humans? d. According to this model, when will world population reach 90 of carrying capacity? Round to the nearest year. Note: This represents a rather naive analysis of world population.arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Functions and Change: A Modeling Approach to Coll...AlgebraISBN:9781337111348Author:Bruce Crauder, Benny Evans, Alan NoellPublisher:Cengage Learning
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
College Algebra
Algebra
ISBN:9781305115545
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
Functions and Change: A Modeling Approach to Coll...
Algebra
ISBN:9781337111348
Author:Bruce Crauder, Benny Evans, Alan Noell
Publisher:Cengage Learning
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning
Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill
Solve ANY Optimization Problem in 5 Steps w/ Examples. What are they and How do you solve them?; Author: Ace Tutors;https://www.youtube.com/watch?v=BfOSKc_sncg;License: Standard YouTube License, CC-BY
Types of solution in LPP|Basic|Multiple solution|Unbounded|Infeasible|GTU|Special case of LP problem; Author: Mechanical Engineering Management;https://www.youtube.com/watch?v=F-D2WICq8Sk;License: Standard YouTube License, CC-BY
Optimization Problems in Calculus; Author: Professor Dave Explains;https://www.youtube.com/watch?v=q1U6AmIa_uQ;License: Standard YouTube License, CC-BY
Introduction to Optimization; Author: Math with Dr. Claire;https://www.youtube.com/watch?v=YLzgYm2tN8E;License: Standard YouTube License, CC-BY