Chapter 16, Problem 33P

Recent interest in competitive and recreational cycling has meant that engineers have directed their skills toward the designand testing of mountain bikes (Fig. P16.33a). Suppose that you are given the task of predicting the horizontal and vertical displacement of a bike bracketing system in response to a force. Assume the forces you must analyze can be simplified as depicted in Fig. P16.33b. You are interested in testing the response of the truss to a force exerted in any number of directions designated by the angle $\theta$. The parameters for the problem are $E=\text{Young's modulus}=\text{2}\times {\text{10}}^{\text{11}}\text{Pa},$ $A=cross-sectionalarea$ $=0.0001{\text{m}}^2,$ $w=\text{width=0}\text{.44m,}$ $\text{L}=\text{length}=\text{0}\text{.56m,}$ and $h=\text{height }0.5\text{ m}$. The displacements x and y can be solved by determining the values that yield a minimum potential energy. Determine the displacements for a force of 10,000 N and a range of $\theta \text{'}s$ from $0°$ (horizontal) to 908 (vertical).

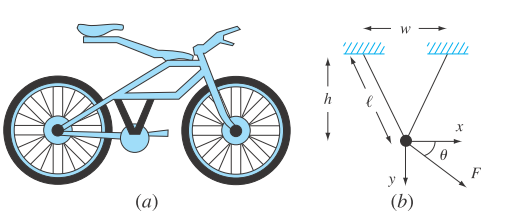
FIGURE P16.33

(a) A mountain bike along with (b) a free-body diagram for a part of the frame.

To determine

To calculate: The minimum potential energy with displacement $x\text{and}y$ for a force of $10,000\text{N}$ and the range of $\theta$’s from $0°\left(\text{horizontal}\right)\text{to}90°\left(\text{vertical}\right)$ if the parameters are given as Young’s modulus E is $2\times {10}^{11}\text{Pa}$, Cross-sectional area A is $0.0001{\text{m}}^{\text{2}}$, width w is $0.44\text{m}$, length l is $0.56\text{m}$ and height h is $0.5\text{m}$. The below figure show the free-body diagram for a part of the frame,

Answer to Problem 33P

Solution:

The minimum potential energy with displacement $x=0.000786\text{and}y=0.0000878$ is $-3.62\text{J}$.

Explanation of Solution

Given Information:

The parameters are given as Young’s modulus E is $2\times {10}^{11}\text{Pa}$, Cross-sectional area A is $0.0001{\text{m}}^{\text{2}}$, width w is $0.44\text{m}$, length l is $0.56\text{m}$ and height h is $0.5\text{m}$. The below figure show the free-body diagram for a part of the frame,

Calculation:

Consider the free body diagram,

The potential energy at a position where horizontal displacement is x and vertical displacement is y, first consider the angular deflection of the bracket and then use the concept of energy stored in a bracket system due to deflection.

$V\left(x,y\right)=\frac{EA}{l}{\left(\frac{w}{2l}\right)}^2{x}^2+\frac{EA}{l}{\left(\frac{h}{l}\right)}^2{y}^2-Fx\cos \theta -Fy\sin \theta$ …… (1)

For $\theta =30°$,

Substitute the values $E=2\times {10}^{11},A=0.0001,w=0.44,l=0.56,F=10000\text{and}h=0.5$ in above equation,

$\begin{array}{c}V\left(x,y\right)=\frac{\left(2\times {10}^{11}\right)\left(0.0001\right)}{0.56}{\left(\frac{0.44}{2\left(0.56\right)}\right)}^2{x}^2+\frac{\left(2\times {10}^{11}\right)\left(0.0001\right)}{0.56}{\left(\frac{0.5}{0.56}\right)}^2{y}^2-\left(10000\right)x\cos \left(30°\right)-\left(10000\right)y\sin \left(30°\right)\\ =5,512,026x^2+28,471,210y^2-8660x-5000y\end{array}$

To minimize this, the excel solver can be used to solve for the displacement.

The excel solver steps are,

Step 1. Initiate quantity $x\text{and}y=0$ and then write the parameter as shown below,

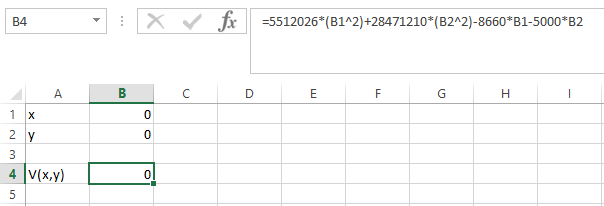
Step 2. Apply the formula in $V\left(x,y\right)$ as shown below,

Step 3. Go to DATA and then click on Solver. This dialog box will appear.

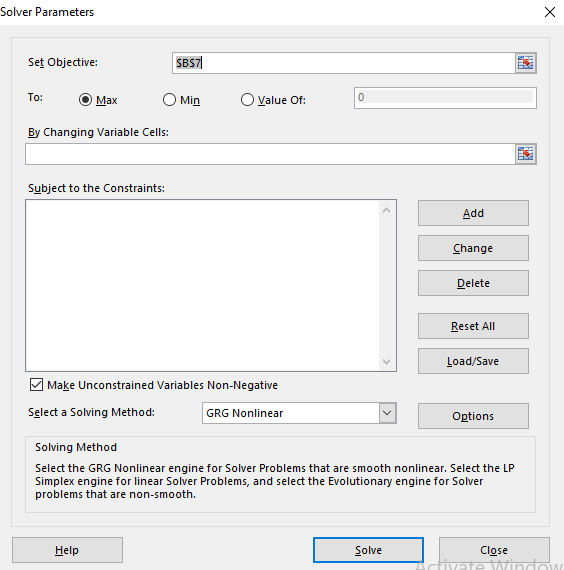
Step 4. Select the set objective, min, changing variable then this dialog box appears.

Step 5. Click on Solve and then OK.

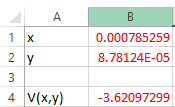
Hence, the minimum potential energy with displacement $x=0.000786\text{and}y=0.0000878$ is $-3.62$.

Put $\theta =0°$ in equation (1),

$\begin{array}{c}V\left(x,y\right)=\frac{\left(2\times {10}^{11}\right)\left(0.0001\right)}{0.56}{\left(\frac{0.44}{2\left(0.56\right)}\right)}^2{x}^2+\frac{\left(2\times {10}^{11}\right)\left(0.0001\right)}{0.56}{\left(\frac{0.5}{0.56}\right)}^2{y}^2-\left(10000\right)x\cos \left(0°\right)-\left(10000\right)y\sin \left(0°\right)\\ =5,512,026x^2+28,471,210y^2-10000x\end{array}$

The potential energy can be found out with upper procedure as $-4.53\text{J}$ and for $\theta =90°$, the equation will be,

$\begin{array}{c}V\left(x,y\right)=\frac{\left(2\times {10}^{11}\right)\left(0.0001\right)}{0.56}{\left(\frac{0.44}{2\left(0.56\right)}\right)}^2{x}^2+\frac{\left(2\times {10}^{11}\right)\left(0.0001\right)}{0.56}{\left(\frac{0.5}{0.56}\right)}^2{y}^2-\left(10000\right)x\cos \left(90°\right)-\left(10000\right)y\sin \left(90°\right)\\ =5,512,026x^2+28,471,210y^2-10000y\end{array}$

The potential energy will be $-0.87\text{J}$.

Thus from the above analysis, it can be concluded that x deflection is maximum when load is pointed in the x direction and y deflection is maximum when load is pointed in the y direction.

However x deflection is more than y direction as potential energy is higher at lower angle.

This can also be concluded that if w values increases then deflection would be more uniform throughout.