
Concept explainers
In the short story The Pit and the Pendulum by 19th-century American horror writer Edgar Allen Poe, a man is tied to a table directly below a swinging pendulum that is slowly lowered toward him. The “bob” of the pendulum is a 1-ft steel scythe connected to a 30-ft brass rod. When the man first sees the pendulum, the pivot is roughly 1 ft above the scythe so that a 29-ft length of the brass rod oscillates above the pivot (Fig. P16.39A). The man escapes when the pivot is near the end of the brass rod (Fig. P16.39B). a. Model the pendulum as a particle of mass ms 5 2 kg attached to a rod of mass mr 5 160 kg. Find the pendulum’s center of mass and rotational inertia around an axis through its center of mass. (Check your answers by finding the center of mass and rotational inertia of just the brass rod.) b. What is the initial period of the pendulum? c. The man saves himself by smearing food on his ropes so that rats chew through them. He does so when he has no more than 12 cycles before the pendulum will make contact with him. How much time does it take the rats to chew through the ropes?
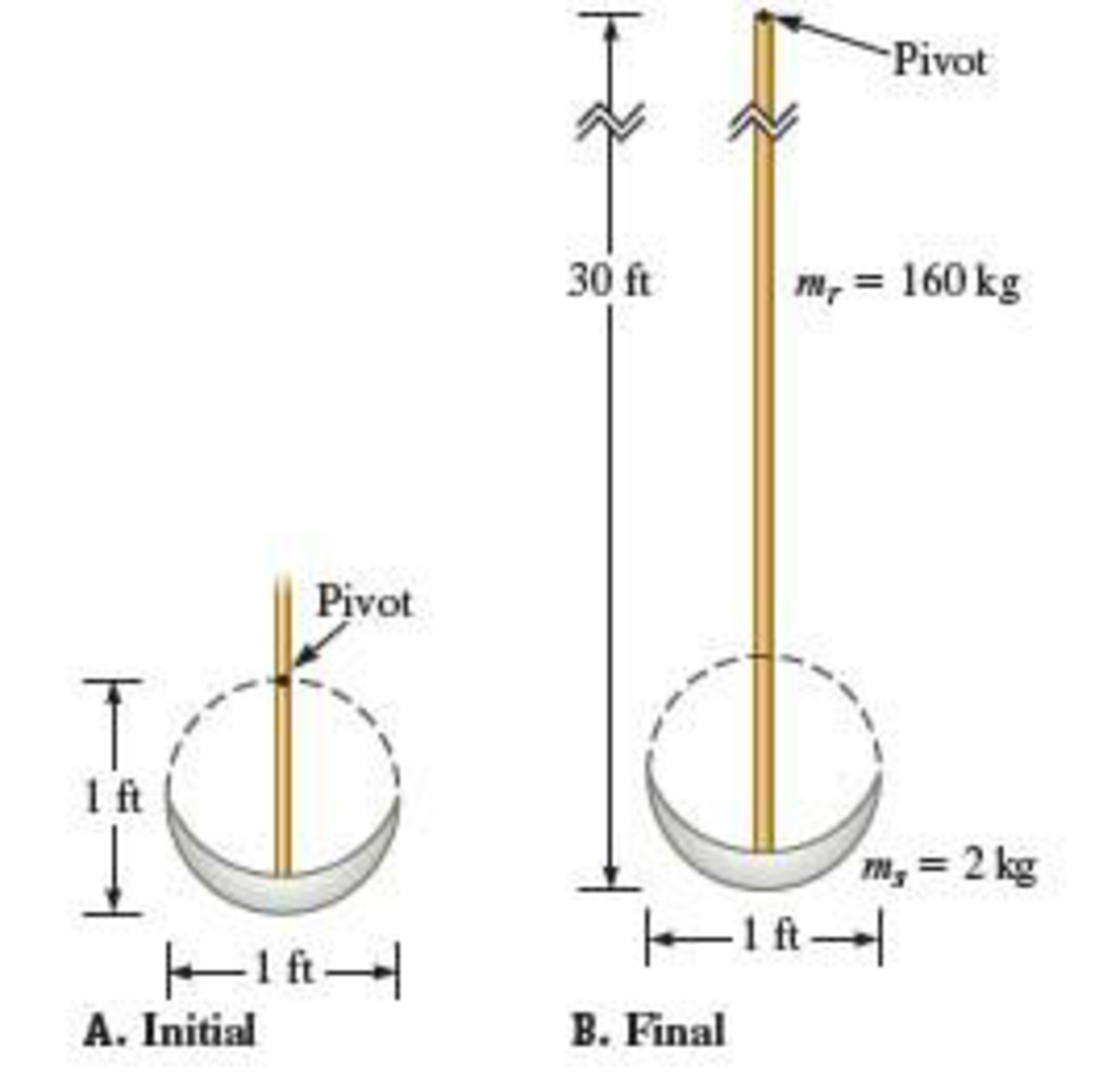
FIGURE P16.39
(a)
The center of mass and the rotational inertia around an axis through its center of mass.
Answer to Problem 39PQ
The center of mass and the rotational inertia around an axis of the pendulum through its center of mass. are
Explanation of Solution
Write the expression for the center of mass of the entire pendulum.
Here,
To find the pendulum’s rotational inertia around its center of mass , add the rods rotational inertia plus the particles rotational inertia. The particles distance from the center of mass is
Here,
To find the
Here,
According to parallel axis theorem, the rotational inertia around the pendulums center of mass can be calculated.
Here,
Write the expression for the moment of inertia.
Use equation (V) in equation (III),
Use equation (III) in equation (IV),
Conclusion:
Substitute
Substitute
Substitute
Therefore, the center of mass and the rotational inertia around an axis of the pendulum through its center of mass. are
(b)
The initial period of the pendulum.
Answer to Problem 39PQ
The initial period of the pendulum is
Explanation of Solution
Write the expression for the period of the pendulum.
Here,
Write the expression for the angular frequency of a physical pendulum.
Here,
The pendulum is a physical pendulum, the distance between the pivot and the center of mass can be found out from the figure given below.
The rotational inertia of the pendulum around the pivot is given by,
Conclusion:
Substitute
to find
Substitute
Substitute
Therefore, The initial period of the pendulum is
(c)
The time taken for the rats to chew through the ropes.
Answer to Problem 39PQ
The time taken for the rats to chew through the ropes is
Explanation of Solution
Write the expression for the period of the pendulum.
Here,
Write the expression for the angular frequency of a physical pendulum.
Here,
The pendulum is a physical pendulum, the distance between the pivot and the center of mass can be found out from the figure given below.
The rotational inertia of the pendulum around the pivot is given by,
Conclusion:
Substitute
To find
Substitute
Substitute
The rats have 12 cycles to chew through the rope or the corresponding tome is,
Therefore, The time taken for the rats to chew through the ropes is
Want to see more full solutions like this?
Chapter 16 Solutions
EBK PHYSICS FOR SCIENTISTS AND ENGINEER
- No chatgpt pls will upvote Already got wrong chatgpt answerarrow_forwardPART III - RESISTORS IN PARALLEL Consider (but do not yet build) the circuit shown in the circuit diagram to the left, which we will call Circuit 3. Make sure you are using Bert bulbs. You may want to wire two batteries in series rather than use a single battery. 7. Predict: a) How will the brightness of bulb B3A compare to the brightness to bulb B3B? c) X E B3A b) How will the brightness of bulb BзA compare to the brightness of bulb B₁ from Circuit 1? How will the currents at points X, Y, and Z be related? www d) How will the current at point X in this circuit compare to the current at point X from Circuit 1? Y Z B3B wwwarrow_forwardPART II - RESISTORS IN SERIES Consider (but do not yet build) the circuit shown in the circuit diagram to the left, which we will call Circuit 2. Make sure you are using Bert bulbs. You may want to wire two batteries in series rather than use a single battery. 4. Predict: a) How will the brightness of bulb B₂ compare to the brighness to bulb B2B? X B2A E Y B2B Ꮓ b) How will the brightness of bulb B2A compare to the brightness of bulb B₁ from Circuit 1? c) How will the currents at points X, Y, and Z be related? d) How will the current at point X in this circuit compare to the current at point X from Circuit 1?arrow_forward
- No chatgpt pls will upvote Already got wrong chatgpt answerarrow_forwardWhat is the practical benefit (in terms of time savings and efficiency) of defining the potential energy? Be clear about what is required in terms of calculation if we do not use the concept of potential energy.arrow_forwardWhat is the critical angle fir the light travelling from the crown glass(n=1.52) into the air(n=1.00)?arrow_forward
- No chatgpt pls will upvotearrow_forwardYou are working with a team that is designing a new roller coaster-type amusement park ride for a major theme park. You are present for the testing of the ride, in which an empty 150 kg car is sent along the entire ride. Near the end of the ride, the car is at near rest at the top of a 100 m tall track. It then enters a final section, rolling down an undulating hill to ground level. The total length of track for this final section from the top to the ground is 250 m. For the first 230 m, a constant friction force of 370 N acts from computer-controlled brakes. For the last 20 m, which is horizontal at ground level, the computer increases the friction force to a value required for the speed to be reduced to zero just as the car arrives at the point on the track at which the passengers exit. (a) Determine the required constant friction force (in N) for the last 20 m for the empty test car. Write AK + AU + AE int = W+Q + TMW + TMT + TET + TER for the car-track-Earth system and solve for…arrow_forward= 12 kg, and m3 Three objects with masses m₁ = 3.8 kg, m₂ find the speed of m3 after it moves down 4.0 m. m/s 19 kg, respectively, are attached by strings over frictionless pulleys as indicated in the figure below. The horizontal surface exerts a force of friction of 30 N on m2. If the system is released from rest, use energy concepts to m m2 m3 iarrow_forward
 University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University
University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Modern PhysicsPhysicsISBN:9781111794378Author:Raymond A. Serway, Clement J. Moses, Curt A. MoyerPublisher:Cengage Learning
Modern PhysicsPhysicsISBN:9781111794378Author:Raymond A. Serway, Clement J. Moses, Curt A. MoyerPublisher:Cengage Learning Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning
Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning





