Chapter 16, Problem 39PQ

In the short story The Pit and the Pendulum by 19th-century American horror writer Edgar Allen Poe, a man is tied to a table directly below a swinging pendulum that is slowly lowered toward him. The “bob” of the pendulum is a 1-ft steel scythe connected to a 30-ft brass rod. When the man first sees the pendulum, the pivot is roughly 1 ft above the scythe so that a 29-ft length of the brass rod oscillates above the pivot (Fig. P16.39A). The man escapes when the pivot is near the end of the brass rod (Fig. P16.39B). a. Model the pendulum as a particle of mass m_s 5 2 kg attached to a rod of mass m_r 5 160 kg. Find the pendulum’s center of mass and rotational inertia around an axis through its center of mass. (Check your answers by finding the center of mass and rotational inertia of just the brass rod.) b. What is the initial period of the pendulum? c. The man saves himself by smearing food on his ropes so that rats chew through them. He does so when he has no more than 12 cycles before the pendulum will make contact with him. How much time does it take the rats to chew through the ropes?

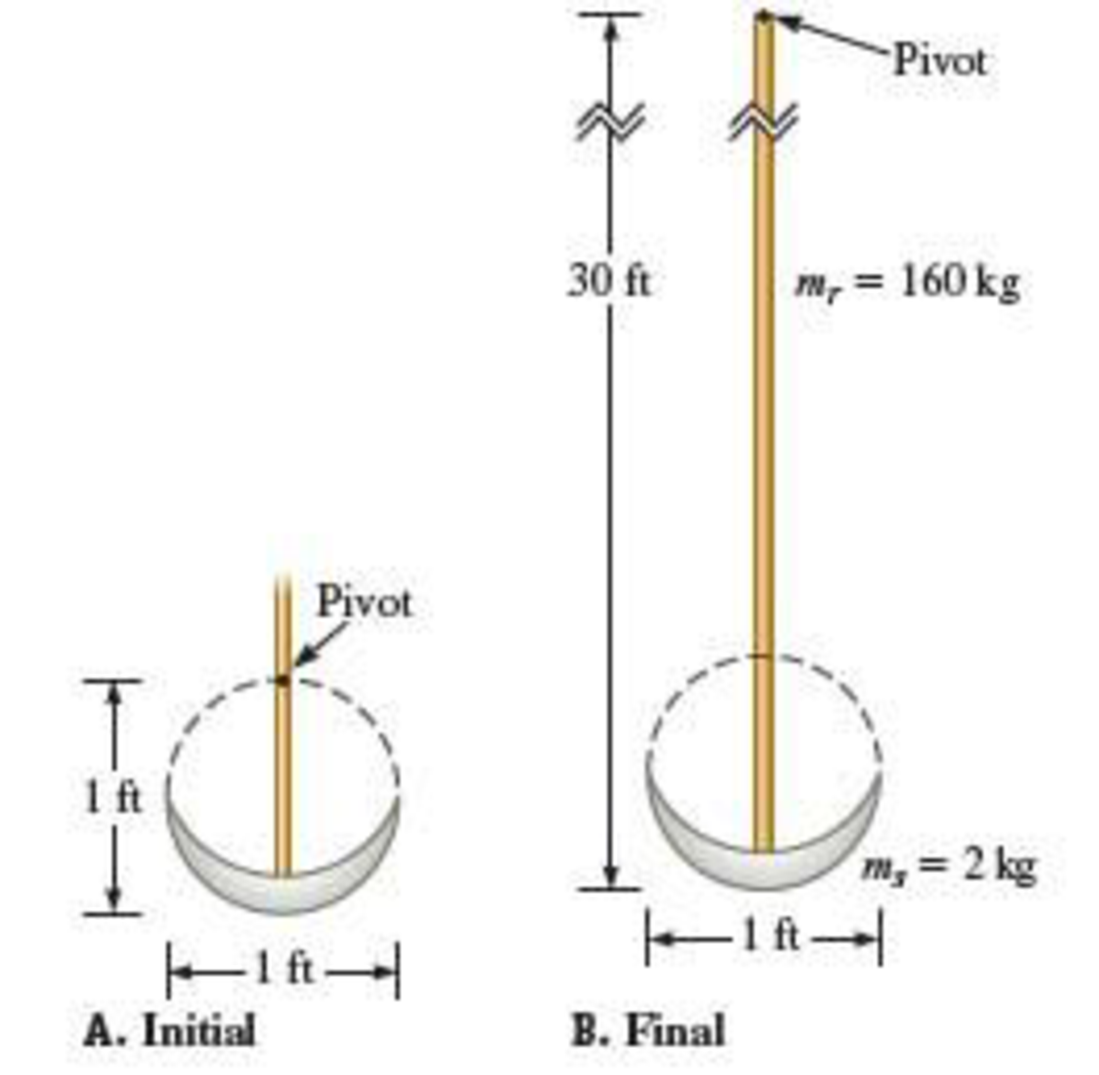
FIGURE P16.39

To determine

The center of mass and the rotational inertia around an axis through its center of mass.

Answer to Problem 39PQ

The center of mass and the rotational inertia around an axis of the pendulum through its center of mass. are $\underset{\_}{4.7\text{m}}$ and $\underset{\_}{1.1\times {10}^3\text{kg}\cdot {\text{m}}^2}$.

Explanation of Solution

Write the expression for the center of mass of the entire pendulum.

    $y_{\text{CM}}=\frac{1}{M}{\displaystyle \sum _{j=1}^n{m}_j{y}_j}$                                                                                                  (I)

Here, $y_{\text{CM}}$ is the center of mass of the entire pendulum, $M$ is the sum of the masses of all the particles, $m_j$ is the mass of the $j$ th particle.

    $y_{\text{CM}}=\frac{1}{M}\left(\frac{m_1{r}_1+m_2{r}_2}{m_1+m_2}\right)$                                                                                       (II)

To find the pendulum’s rotational inertia around its center of mass , add the rods rotational inertia plus the particles rotational inertia. The particles distance from the center of mass is $4.4\text{m}$.

    $I_{\text{CM}}=I_{\text{particle}}+I_{\text{rod}}$                                                                                                (III)

Here, $I_{\text{CM}}$ is the rotational inertia of the pendulum, $I_{\text{particle}}$ is the rotational inertia of the particle, $I_{\text{rod}}$ is the rotational inertia of the rod.

To find the $I_{\text{rod}}$, first find the rotational inertia around an axis through the rods center of mass.

    ${\left(I_{\text{CM}}\right)}_{\text{rod}}=\frac{1}{12}m{L}^2$                                                                                                (III)

Here, $L$ is the length of the rod.

According to parallel axis theorem, the rotational inertia around the pendulums center of mass can be calculated.

    $I_{\text{rod}}={\left(I_{\text{CM}}\right)}_{\text{rod}}+m{h}^2$                                                                                           (IV)

Here, $h$ is the perpendicular distance between a new rotation axis and the axis through the center of mass.

Write the expression for the moment of inertia.

    $I_{\text{particle}}=m{r}^2$                                                                                                          (V)

Use equation (V) in equation (III),

    $I_{\text{CM}}=M{R}^2+I_{\text{rod}}$                                                                                                 (VI)

Use equation (III) in equation (IV),

    $I_{\text{rod}}=\frac{1}{12}m{L}^2+m{\left(\Delta y_{\text{CM}}\right)}^2$                                                                               (VII)

Conclusion:

Substitute $160\text{kg}$ for $m_1$ and $2\text{kg}$ for $m_2$, $4.6\text{m}$ for $r_1$ and $9.1\text{m}$ for $r_2$ in equation (II) to find $y_{\text{CM}}$.

    $\begin{array}{c}{y}_{\text{CM}}=\frac{\left(160\text{kg}\right)\left(4.6\text{m}\right)+\left(2\text{kg}\right)\left(9.1\text{m}\right)}{160\text{kg}+\text{2}\text{kg}}\\ =4.7\text{m}\end{array}$

Substitute $160\text{kg}$ for $m$ and $0.1\text{m}$ for $h$ in equation (VII) to find $I_{\text{rod}}$.

    $\begin{array}{c}{I}_{\text{rod}}=\frac{1}{12}\left(160\text{kg}\right){\left(9.1\text{m}\right)}^2+\left(160\text{kg}\right){\left(0.1\text{m}\right)}^2\\ =1105.73\text{kg}\cdot {\text{m}}^2\end{array}$

Substitute $2\text{kg}$ for $m$ , $4.4\text{m}$ for $r$ and $1105.73\text{kg}\cdot {\text{m}}^2$ for $I_{\text{rod}}$ in equation (VI)to find $I_{\text{CM}}$.

    $\begin{array}{c}{I}_{\text{CM}}=\left(2\text{kg}\right){\left(4.4\text{m}\right)}^2+1105.73\text{kg}\cdot {\text{m}}^2\\ =1.14\times {10}^3\text{kg}\cdot {\text{m}}^2\\ \approx 1.1\times {10}^3\text{kg}\cdot {\text{m}}^2\end{array}$

Therefore, the center of mass and the rotational inertia around an axis of the pendulum through its center of mass. are $\underset{\_}{4.7\text{m}}$ and $\underset{\_}{1.1\times {10}^3\text{kg}\cdot {\text{m}}^2}$.

To determine

The initial period of the pendulum.

Answer to Problem 39PQ

The initial period of the pendulum is $\underset{\_}{4.8\text{s}}$.

Explanation of Solution

Write the expression for the period of the pendulum.

    $T=\frac{2\pi }{{\omega }_{\text{phy}}}$                                                                                                             (VIII)

Here, $T$ is the time period of the pendulum, ${\omega }_{\text{phy}}$ is the angular frequency of the pendulum.

Write the expression for the angular frequency of a physical pendulum.

    ${\omega }_{\text{phy}}=\sqrt{\frac{Mg{r}_{\text{CM}}}{I}}$                                                                                                  (IX)

Here, $I$ is the rotational inertia of the pivot.

The pendulum is a physical pendulum, the distance between the pivot and the center of mass can be found out from the figure given below.

The rotational inertia of the pendulum around the pivot is given by,

    $I_{\text{pivot}}=I_{\text{CM}}+M{r}_{\text{CM}}^2$                                                                                               (X)

Conclusion:

Substitute $1.1\times {10}^3\text{kg}\cdot {\text{m}}^2$ for $I_{\text{CM}}$, $162\text{kg}$ for $M$ and $4.1\text{m}$ for $r_{\text{CM}}$, in equation (X)

to find $I_{\text{pivot}}$.

    $\begin{array}{c}{I}_{\text{pivot}}=\left(1.1\times {10}^3\text{kg}\cdot {\text{m}}^2\right)+162\text{kg}{\left(4.1\text{m}\right)}^2\\ =3.8\times {10}^3\text{kg}\cdot {\text{m}}^2\end{array}$

Substitute $3.8\times {10}^3\text{kg}\cdot {\text{m}}^2$ for $I$ , $162\text{kg}$ for $M$, $9.81\text{m}/{\text{s}}^2$ for $g$ , $4.1\text{m}$ for $r_{\text{CM}}$ in equation (IX) to find ${\omega }_{\text{phy}}$.

    $\begin{array}{c}{\omega }_{\text{phy}}=\sqrt{\frac{\left(162\text{kg}\right)\left(9.81\text{m}/{\text{s}}^2\right)\left(4.1\text{m}\right)}{\left(3.8\times {10}^3\text{kg}\cdot {\text{m}}^2\right)}}\\ =1.3\text{rad}/\text{s}\end{array}$

Substitute $1.3\text{rad}/\text{s}$ for ${\omega }_{\text{phy}}$ in equation (IX) to find $T$.

    $\begin{array}{c}T=\frac{2\pi }{\left(1.3\text{rad}/\text{s}\right)}\\ =4.8\text{s}\end{array}$

Therefore, The initial period of the pendulum is $\underset{\_}{4.8\text{s}}$.

To determine

The time taken for the rats to chew through the ropes.

Answer to Problem 39PQ

The time taken for the rats to chew through the ropes is $\underset{\_}{60\text{s}}$.

Explanation of Solution

Write the expression for the period of the pendulum.

    $T=\frac{2\pi }{{\omega }_{\text{phy}}}$                                                                                                             (VIII)

Here, $T$ is the time period of the pendulum, ${\omega }_{\text{phy}}$ is the angular frequency of the pendulum.

Write the expression for the angular frequency of a physical pendulum.

    ${\omega }_{\text{phy}}=\sqrt{\frac{Mg{r}_{\text{CM}}}{I}}$                                                                                                 (IX)

Here, $I$ is the rotational inertia of the pivot.

The pendulum is a physical pendulum, the distance between the pivot and the center of mass can be found out from the figure given below.

The rotational inertia of the pendulum around the pivot is given by,

    $I_{\text{pivot}}=I_{\text{CM}}+M{r}_{\text{CM}}^2$                                                                                               (X)

Conclusion:

Substitute $1.1\times {10}^3\text{kg}\cdot {\text{m}}^2$ for $I_{\text{CM}}$, $162\text{kg}$ for $M$ and $4.7\text{m}$ for $r_{\text{CM}}$, in equation (X)

To find $I_{\text{pivot}}$.

    $\begin{array}{c}{I}_{\text{pivot}}=\left(1.1\times {10}^3\text{kg}\cdot {\text{m}}^2\right)+162\text{kg}{\left(4.7\text{m}\right)}^2\\ =4.7\times {10}^3\text{kg}\cdot {\text{m}}^2\end{array}$

Substitute $3.8\times {10}^3\text{kg}\cdot {\text{m}}^2$ for $I$ , $162\text{kg}$ for $M$, $9.81\text{m}/{\text{s}}^2$ for $g$ , $4.1\text{m}$ for $r_{\text{CM}}$ in equation (IX) to find ${\omega }_{\text{phy}}$.

    $\begin{array}{c}{\omega }_{\text{phy}}=\sqrt{\frac{\left(162\text{kg}\right)\left(9.81\text{m}/{\text{s}}^2\right)\left(4.7\text{m}\right)}{\left(4.7\times {10}^3\text{kg}\cdot {\text{m}}^2\right)}}\\ =1.3\text{rad}/\text{s}\end{array}$

Substitute $1.3\text{rad}/\text{s}$ for ${\omega }_{\text{phy}}$ in equation (IX) to find $T$.

    $\begin{array}{c}T=\frac{2\pi }{\left(1.3\text{rad}/\text{s}\right)}\\ =5.0\text{s}\end{array}$

The rats have 12 cycles to chew through the rope or the corresponding tome is,

  $12\times 5.0\text{s}=60\text{s}$

Therefore, The time taken for the rats to chew through the ropes is $\underset{\_}{60\text{s}}$.