
AtotalchargeQ is uniformly distributed around a ring-shaped conductor with radius a. A charge q is located at a distance x from the center of the ring (Fig. P16.23). The force exerted on the charge by the ring is given by
Where
0.9m Determine the distance x where the force is a maximum.
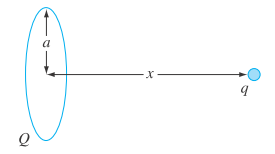
FIGURE P16.23
Want to see the full answer?
Check out a sample textbook solution
Chapter 16 Solutions
EBK NUMERICAL METHODS FOR ENGINEERS
- Consider the weighted voting system [11: 7, 4, 1]Find the Shapley-Shubik power distribution of this weighted voting system.List the power for each player as a fraction: P1: P2: P3:arrow_forwardConsider the weighted voting system [18: 15, 8, 3, 1]Find the Banzhaf power distribution of this weighted voting system.List the power for each player as a fraction: P1: P2: P3: P4:arrow_forwardConsider the weighted voting system [18: 15, 8, 3, 1]Find the Banzhaf power distribution of this weighted voting system.List the power for each player as a fraction: P1 = P2 = P3 = P4 =arrow_forward
- Consider the weighted voting system [18: 15, 8, 3, 1]Find the Banzhaf power distribution of this weighted voting system.List the power for each player as a fraction: P1: P2: P3: P4:arrow_forwardConsider the weighted voting system [18: 15, 8, 3, 1]Find the Banzhaf power distribution of this weighted voting system.List the power for each player as a fraction: P1: P2: P3: P4:arrow_forwardFind the Banzhaf power distribution of the weighted voting system[26: 19, 15, 11, 6]Give each player's power as a fraction or decimal value P1 = P2 = P3 = P4 =arrow_forward
- solve it using augmented matrix. Also it is homeworkarrow_forward4. Now we'll look at a nonhomogeneous example. The general form for these is y' + p(x)y = f(x). For this problem, we will find solutions of the equation +2xy= xe (a) Identify p(x) and f(x) in the equation above. p(x) = f(x) = (b) The complementary equation is y' + p(x)y = 0. Write the complementary equation. (c) Find a solution for the complementary equation. We'll call this solution y₁. (You only need one particular solution, so you can let k = 0 here.) Y1 = (d) Check that y₁ satisfies the complementary equation, in other words, that y₁+ p(x)y₁ = 0.arrow_forwarddata managementarrow_forward
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
 Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
 Elements Of Modern AlgebraAlgebraISBN:9781285463230Author:Gilbert, Linda, JimmiePublisher:Cengage Learning,
Elements Of Modern AlgebraAlgebraISBN:9781285463230Author:Gilbert, Linda, JimmiePublisher:Cengage Learning,



