Precalculus: Concepts Through Functions, A Unit Circle Approach to Trigonometry (4th Edition)
4th Edition
ISBN: 9780134686974
Author: Michael Sullivan, Michael Sullivan III
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 1.6, Problem 23AYU
23. Time Required to Go from an Island to a Town An island is 2 miles from the nearest point P on a straight shoreline. A town is 12 miles down the shore from P. See the illustration.
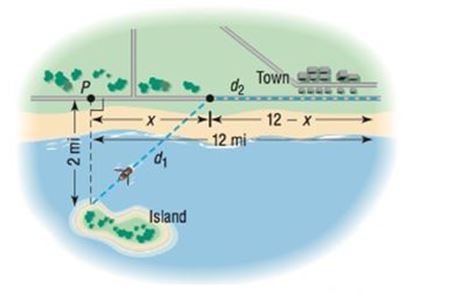
(a) If a person can row a boat at an average speed of 3 miles per hour and the same person can walk 5 miles per hour, build a model that expresses the time T that it takes to go from the island to town as a function of the distance X from P to where the person lands the boat.
(b) What is the domain of Τ?
(c) How long will it take to travel from the island to town if the person lands the boat 4 miles from P?
(d) How long will it take if the person lands the boat 8 miles from Ρ?
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
An airplane flies due west at an airspeed of 428 mph. The wind blows in the direction of 41° south of west
at 50 mph. What is the ground speed of the airplane? What is the bearing of the airplane?
A vector with magnitude 5 points in a direction 190 degrees counterclockwise from the positive x axis.
Write the vector in component form, and show your answers accurate to 3 decimal places.
||A||=23
45°
Find the EXACT components of the vector above using the angle shown.
Chapter 1 Solutions
Precalculus: Concepts Through Functions, A Unit Circle Approach to Trigonometry (4th Edition)
Ch. 1.1 - The inequality 1x3 can be written in interval...Ch. 1.1 - 2. If , the value of the expression is _______ ...Ch. 1.1 - 3. The domain of the variable in the expression is...Ch. 1.1 - 4. Solve the inequality: . Graph the solution set....Ch. 1.1 - To rationalize the denominator of 3 5 2 , multiply...Ch. 1.1 - 6. A quotient is considered rationalized if its...Ch. 1.1 - If f is a function defined by the equation y=f(x),...Ch. 1.1 - If f(x)=x+1 and g(x)=x3, then ____________x3(x+1).Ch. 1.1 - True or False Every relation is a function.Ch. 1.1 - True or False The domain (f.g)(x) consists of the...
Ch. 1.1 - 13. True or False If no domains is specified for a...Ch. 1.1 - True or False The domain of the function f(x)=x24x...Ch. 1.1 - 8. If the domain of f is all real numbers in the...Ch. 1.1 - 9. The domain of consists of numbers x for which...Ch. 1.1 - The set of all images of the elements in the...Ch. 1.1 - 16. The independent variable is sometimes...Ch. 1.1 - The expression f(x+h)f(x)h is called the...Ch. 1.1 - When written as y=f(x), a function is said to be...Ch. 1.1 - In Problems 19-30, state the domain and range for...Ch. 1.1 - In Problems 19-30, state the domain and range for...Ch. 1.1 - In Problems 19-30, state the domain and range for...Ch. 1.1 - In Problems 19-30, state the domain and range for...Ch. 1.1 - In Problems 19-30, state the domain and range for...Ch. 1.1 - In Problems 19-30, state the domain and range for...Ch. 1.1 - In Problems 19-30, state the domain and range for...Ch. 1.1 - In Problems 19-30, state the domain and range for...Ch. 1.1 - In problem 19-30, state the domain and range for...Ch. 1.1 - In Problems 19-30, state the domain and range for...Ch. 1.1 - In Problems 19-30, state the domain and range for...Ch. 1.1 - In Problems 19-30, state the domain and range for...Ch. 1.1 - In Problems 19-30, state the domain and range for...Ch. 1.1 - In Problems 31-42, determine whether the equation...Ch. 1.1 - In Problems 31-42, determine whether the equation...Ch. 1.1 - In Problems 31-42, determine whether the equation...Ch. 1.1 - In problem 31-42 determine whether the equation...Ch. 1.1 - In Problems 31-42, determine whether the equation...Ch. 1.1 - In Problems 31-42, determine whether the equation...Ch. 1.1 - In Problems 31-42, determine whether the equation...Ch. 1.1 - In Problems 31-42, determine whether the equation...Ch. 1.1 - In Problems 31-42, determine whether the equation...Ch. 1.1 - In Problems 31-42, determine whether the equation...Ch. 1.1 - In Problems 31-42, determine whether the equation...Ch. 1.1 - In problems 43-50, find the following for each...Ch. 1.1 -
In problems 43-50, find the following for each...Ch. 1.1 -
In problems 43-50, find the following for each...Ch. 1.1 -
In problems 43-50, find the following for each...Ch. 1.1 - In problems 43-50, find the following for each...Ch. 1.1 -
In problems 43-50, find the following for each...Ch. 1.1 - In problems 43-50, find the following for each...Ch. 1.1 - In problems 43-50, find the following for each...Ch. 1.1 - In Problems 51-66, find the domain of each...Ch. 1.1 - In Problems 51-66, find the domain of each...Ch. 1.1 - In problem 51-66, find the domain of each...Ch. 1.1 - In Problems 51-66, find the domain of each...Ch. 1.1 - In Problems 51-66, find the domain of each...Ch. 1.1 - In Problems 51-66, find the domain of each...Ch. 1.1 - In Problems 51-66, find the domain of each...Ch. 1.1 - In Problems 51-66, find the domain of each...Ch. 1.1 - In Problems 51-66, find the domain of each...Ch. 1.1 - In Problems 51-66, find the domain of each...Ch. 1.1 - In problem 51-66, find the domain of each...Ch. 1.1 - In Problems 51 – 66, find the domain of each...Ch. 1.1 - In Problems 51-66, find the domain of each...Ch. 1.1 - In Problems 51-66, find the domain of each...Ch. 1.1 - In Problems 51-66, find the domain of each...Ch. 1.1 - In Problems 51-66, find the domain of each...Ch. 1.1 - In problems 67-76, for the given functions f and...Ch. 1.1 - In problems 67-76, for the given functions f and...Ch. 1.1 - In problems 67-76, for the given functions f and...Ch. 1.1 - In problems 67-76, for the given functions f and...Ch. 1.1 - In problems 67-76, for the given functions f and g...Ch. 1.1 - In problems 67-76, for the given functions f and g...Ch. 1.1 - In problems 67-76, for the given functions f and g...Ch. 1.1 - In problems 67-76, for the given functions f and g...Ch. 1.1 - In problems 67-76, for the given functions f and...Ch. 1.1 - In problems 67-76, for the given functions f and...Ch. 1.1 - 77. Given and , find the function g.
Ch. 1.1 - 78. Given and , find the function g.
Ch. 1.1 - In Problems 79-90, find the difference quotient of...Ch. 1.1 - In Problems 79-90, find the difference quotient of...Ch. 1.1 - In Problems 79-90, find the difference quotient of...Ch. 1.1 - In Problems 79-90, find the difference quotient of...Ch. 1.1 - In Problems 79-90, find the difference quotient of...Ch. 1.1 - In Problems 79-90, find the difference quotient of...Ch. 1.1 - In Problems 79-90, find the difference quotient of...Ch. 1.1 - In Problems 79-90, find the difference quotient of...Ch. 1.1 - In Problems 79-90, find the difference quotient of...Ch. 1.1 - In Problems 79-90, find the difference quotient of...Ch. 1.1 - In problem 79-90, find the difference quotient of...Ch. 1.1 - In Problems 79-90, find the difference quotient of...Ch. 1.1 - 91. Given , find the value(s) for x such that...Ch. 1.1 - 92. Given , find the value(s) for x such that...Ch. 1.1 - If f( x )=2 x 3 +A x 2 +4x-5 and f( 2 )=5 , what...Ch. 1.1 - If f( x )=3 x 2 -Bx+4 and f( 1 )=12 , what is the...Ch. 1.1 - 95. If and , what is the value of A?
Ch. 1.1 - If f( x )= 2x-B 3x+4 and f( 2 )= 1 2 , what is the...Ch. 1.1 - 97. Geometry Express the area A of a rectangle as...Ch. 1.1 - Geometry Express the area A of an isosceles right...Ch. 1.1 - 99. Constructing Functions Express the gross...Ch. 1.1 - Constructing Functions Ann, a commissioned...Ch. 1.1 - Population as a Function of Age, The function,...Ch. 1.1 - Prob. 102AYUCh. 1.1 - Prob. 103AYUCh. 1.1 - Prob. 104AYUCh. 1.1 - Prob. 105AYUCh. 1.1 - Prob. 106AYUCh. 1.1 - Prob. 107AYUCh. 1.1 - Prob. 108AYUCh. 1.1 - Prob. 109AYUCh. 1.1 - Prob. 110AYUCh. 1.1 - Prob. 111AYUCh. 1.1 - Prob. 112AYUCh. 1.1 - Prob. 113AYUCh. 1.1 - 114. Some functions f have the property that for...Ch. 1.1 - 115. Are the functions and the same? Explain.
...Ch. 1.1 - 116. Investigate when, historically, the use of...Ch. 1.1 - Find a function H that multiplies a number X by 3...Ch. 1.2 - The intercepts of the equation x 2 +4 y 2 =16 are...Ch. 1.2 - Prob. 2AYUCh. 1.2 - Prob. 3AYUCh. 1.2 - Prob. 4AYUCh. 1.2 - Prob. 5AYUCh. 1.2 - Prob. 6AYUCh. 1.2 - Prob. 7AYUCh. 1.2 - Prob. 8AYUCh. 1.2 - Prob. 9AYUCh. 1.2 - Prob. 10AYUCh. 1.2 - Use the given graph of the function to answer...Ch. 1.2 - Use the given graph of the function f to answer...Ch. 1.2 - In Problems 13-24, determine whether the graph is...Ch. 1.2 - In Problems 13-24, determine whether the graph is...Ch. 1.2 - In Problems 13-24, determine whether the graph is...Ch. 1.2 - In Problems 13-24, determine whether the graph is...Ch. 1.2 - In Problems 13-24, determine whether the graph is...Ch. 1.2 - In Problems 13-24, determine whether the graph is...Ch. 1.2 - In Problems 13-24, determine whether the graph is...Ch. 1.2 - In Problems 13-24, determine whether the graph is...Ch. 1.2 - In Problems 13-24, determine whether the graph is...Ch. 1.2 - In Problems 13-24, determine whether the graph is...Ch. 1.2 - In Problems 13-24, determine whether the graph is...Ch. 1.2 - In Problems 13-24, determine whether the graph is...Ch. 1.2 - f(x)=2x2x1 Is the point (1,2) on the graph of f?...Ch. 1.2 - In Problems 25-30, answer the questions about the...Ch. 1.2 - f(x)=x+2x6 Is the point (3,14) on the graph of f?...Ch. 1.2 - f(x)=x2+2x+4 Is the point (1,35) on the graph of...Ch. 1.2 - f(x)=2x2x4+1 Is the point (1,1) on the graph of f?...Ch. 1.2 - f(x)=2x2x4+1 Is the point (12,23) on the graph of...Ch. 1.2 - The graphs of two functions, and are...Ch. 1.2 - Granny Shots The last player in the NBA to use an...Ch. 1.2 - Free-Throw Shots According to physicist Peter...Ch. 1.2 - 34. Cross-sectional Area The cross-sectional area...Ch. 1.2 - Motion οf a Golf Ball A golf ball is hit with an...Ch. 1.2 - 36. Effect of Elevation on Weight If an object...Ch. 1.2 - 37. Cost of Transatlantic Travel A Boeing 747...Ch. 1.2 - Reading and Interpreting Graphs Let be the...Ch. 1.2 - 39. Reading and Interpreting Graphs Let C be the...Ch. 1.2 - Describe how you would find the domain and range...Ch. 1.2 - 41. How many x-intercepts can the graph of a...Ch. 1.2 - Is a graph that consists of a single point the...Ch. 1.2 - Match each of the following functions with the...Ch. 1.2 - Match each of the following functions with the...Ch. 1.2 - 45. Consider the following scenario: Barbara...Ch. 1.2 - 46. Consider the following scenario: Jayne enjoys...Ch. 1.2 - The following sketch represents the distance d (in...Ch. 1.2 - The following sketch represents the speed v (in...Ch. 1.2 - Draw the graph of a function whose domain is { x|...Ch. 1.2 - Is there a function whose graph is symmetric with...Ch. 1.2 - Explain why the vertical-line test works.Ch. 1.3 - ‘Are You Prepared?' Answers are given at the end...Ch. 1.3 - 'Are You Prepared?' Answers are given at the end...Ch. 1.3 - ‘Are You Prepared?' Answers are given at the end...Ch. 1.3 - ‘Are You Prepared?’ Answers are given at the end...Ch. 1.3 - ‘Are You Prepared?' Answers are given at the end...Ch. 1.3 - 6. A function f is _____ on an interval I if, for...Ch. 1.3 - A(n) _____function f is one for which f(x)=f(x)...Ch. 1.3 - 8. True or False A function f is decreasing on an...Ch. 1.3 - 9. State True or False:
A function has a local...Ch. 1.3 - 10. True or False Even functions have graphs that...Ch. 1.3 - 11. An odd function is symmetric with respect to...Ch. 1.3 - 12. Which of the following intervals is required...Ch. 1.3 - Prob. 13AYUCh. 1.3 - In Problems 13-24, use the graph of the function f...Ch. 1.3 - In Problems 13-24, use the graph of the function f...Ch. 1.3 - In Problems 13-24, use the graph of the function f...Ch. 1.3 - In Problems 13-24, use the graph of the function f...Ch. 1.3 - In Problems 13-24, use the graph of the function f...Ch. 1.3 - In Problems 13-24, use the graph of the function f...Ch. 1.3 - In Problems 13-24, use the graph of the function f...Ch. 1.3 - In Problems 13-24, use the graph of the function f...Ch. 1.3 - In Problems 13-24, use the graph of the function f...Ch. 1.3 - In Problems 13-24, use the graph of the function f...Ch. 1.3 - In Problems 13-24, use the graph of the function f...Ch. 1.3 - In Problems 25-32, the graph of a function is...Ch. 1.3 - In Problems 25-32, the graph of a function is...Ch. 1.3 - In Problems 25-32, the graph of a function is...Ch. 1.3 - In Problems 25-32, the graph of a function is...Ch. 1.3 - In Problems 25-32, the graph of a function is...Ch. 1.3 - In Problems 25-32, the graph of a function is...Ch. 1.3 - In Problems 25-32, the graph of a function is...Ch. 1.3 - In Problems 25-32, the graph of a function is...Ch. 1.3 - In Problems 33-36, the graph of a function f is...Ch. 1.3 - In Problems 33-36, the graph of a function f is...Ch. 1.3 - In Problems 33-36, the graph of a function f is...Ch. 1.3 - In problems 33-36 the graph of a function f is...Ch. 1.3 - In Problems 37-48, determine algebraically whether...Ch. 1.3 - In Problems 37-48, determine algebraically whether...Ch. 1.3 - 39. In problem , determine algebraically whether...Ch. 1.3 - In Problems 37-48, determine algebraically whether...Ch. 1.3 - In problem 3748, determine algebraically whether...Ch. 1.3 - In Problems 37-48, determine algebraically whether...Ch. 1.3 - In Problems 37-48, determine algebraically whether...Ch. 1.3 - In Problems 37-48, determine algebraically whether...Ch. 1.3 - In Problems 37-48, determine algebraically whether...Ch. 1.3 - In Problems 37-48, determine algebraically whether...Ch. 1.3 - In Problems 37-48, determine algebraically whether...Ch. 1.3 - In Problems 37-48, determine algebraically whether...Ch. 1.3 - In Problem 49-56, for each graph of a function...Ch. 1.3 - In Problem 49-56, for each graph of a function...Ch. 1.3 - In Problem 49-56, for each graph of a function...Ch. 1.3 - In problems 4956, for each graph of a function...Ch. 1.3 - In Problems 49-56, for each graph of a function ,...Ch. 1.3 - In Problems 49-56, for each graph of a function ,...Ch. 1.3 - In Problems 49-56, for each graph of a function ,...Ch. 1.3 - In Problems 49-56, for each graph of a function ,...Ch. 1.3 - In Problems 57-64, use a graphing utility to graph...Ch. 1.3 - In Problems 57-64, use a graphing utility to graph...Ch. 1.3 - In Problems 57-64, use a graphing utility to graph...Ch. 1.3 - In Problems 57-64, use a graphing utility to graph...Ch. 1.3 - In Problems 57-64, use a graphing utility to graph...Ch. 1.3 - In Problems 57-64, use a graphing utility to graph...Ch. 1.3 - In Problems 57-64, use a graphing utility to graph...Ch. 1.3 - In Problems 57-64, use a graphing utility to graph...Ch. 1.3 - 65. Find the average rate of change of
From to ...Ch. 1.3 - Find the average rate of change of f(x)=x3+1; From...Ch. 1.3 - Find the average rate of change of g(x)=x32x+1;...Ch. 1.3 - Prob. 68AYUCh. 1.3 - 69.
(a) Find the average rate of change from 1...Ch. 1.3 - 70.
(a) Find the average rate of change from 2...Ch. 1.3 - g(x)=x22 Find the average rate of change from 2 to...Ch. 1.3 - g(x)=x2+1 Find the average rate of change from 1...Ch. 1.3 - 73.
Find the average rate of the change from to...Ch. 1.3 - h(x)=2x2+x Find the average rate of change from 0...Ch. 1.3 - 75. g( x )= x 3 27x (a) Determine whether g is...Ch. 1.3 - 76.
(a) Determine whether f is even, odd, or...Ch. 1.3 - F(x)=x4+8x2+9 Determine whether F is even, odd, or...Ch. 1.3 - G(x)=x4+32x2+144 Determine whether G is even, odd,...Ch. 1.3 - 79. Minimum Average Cost The average cost per hour...Ch. 1.3 - 80. Medicine Concentration The concentration C of...Ch. 1.3 - Data Plan Cost The monthly cost , in dollars, for...Ch. 1.3 - National Debts The size of the total debts owed by...Ch. 1.3 - 83. E. coli Growth A strain of E. coli Beu...Ch. 1.3 - e-Filing Tax Returns The Internal Revenue Service...Ch. 1.3 - For the function f(x)=x2, compute the average rate...Ch. 1.3 - For the function f(x)=x2, compute the average rate...Ch. 1.3 - Problems 87-94 require the following discussion...Ch. 1.3 - Problems 87-94 require the following discussion of...Ch. 1.3 - Problems 87-94 require the following discussion of...Ch. 1.3 - Problems 87-94 require the following discussion of...Ch. 1.3 - Problems 87-94 require the following discussion of...Ch. 1.3 - Problems 87-94 require the following discussion of...Ch. 1.3 - Problems 87-94 require the following discussion of...Ch. 1.3 - Problems 87-94 require the following discussion of...Ch. 1.3 - 95. Draw the graph of a function that has the...Ch. 1.3 - 96. Redo Problem 95 with the following additional...Ch. 1.3 - 97. How many x-intercept can a function defined on...Ch. 1.3 - 98. Suppose that a friend of yours does not...Ch. 1.3 - 99. Can a function be both even and odd? Explain.Ch. 1.3 - 100. Using a graphing utility, graph y=5 on the...Ch. 1.3 - 101. A function f has a positive average rate of...Ch. 1.3 - 102. Show that a constant function has an average...Ch. 1.4 - 1. Sketch the graph of . (p. 22)
Ch. 1.4 - 2. Sketch the graph of . (pp. 22-23)
Ch. 1.4 - 3. List the intercepts of the equation . (pp....Ch. 1.4 - The function f( x )= x 2 is decreasing on the...Ch. 1.4 - 5. When functions are defined by more than one...Ch. 1.4 - 6. True or False The cube function is odd and is...Ch. 1.4 - True or False The cube root function is odd and is...Ch. 1.4 - True or False The domain and the range of the...Ch. 1.4 - 9. Which of the following functions has a graph...Ch. 1.4 - Consider the following function. f( x )= 3x2ifx2 x...Ch. 1.4 - In Problems 11-18, match each graph to its...Ch. 1.4 - In Problems 11-18, match each graph to its...Ch. 1.4 - In Problems 11-18, match each graph to its...Ch. 1.4 - In Problems 11-18, match each graph to its...Ch. 1.4 - In Problems 11-18, match each graph to its...Ch. 1.4 - In Problems 11-18, match each graph to its...Ch. 1.4 - In Problems 11-18, match each graph to its...Ch. 1.4 - In Problems 11-18, match each graph to its...Ch. 1.4 - In Problems 19-26, sketch the graph of each...Ch. 1.4 - In Problems 19-26, sketch the graph of each...Ch. 1.4 - In Problems 19-26, sketch the graph of each...Ch. 1.4 - In Problems 19-26, sketch the graph of each...Ch. 1.4 - In Problems 19-26, sketch the graph of each...Ch. 1.4 - In Problems 19-26, sketch the graph of each...Ch. 1.4 - In Problems 19-26, sketch the graph of each...Ch. 1.4 - In Problems 19-26, sketch the graph of each...Ch. 1.4 - 27. If
Find: (a)
(b)
(c)
Ch. 1.4 - In Problems 19-26, sketch the graph of each...Ch. 1.4 - 29. If
Find: (a)
(b)
(c)
...Ch. 1.4 - In Problems 19-26, sketch the graph of each...Ch. 1.4 - In Problems 31-42: (a) Find the domain of each...Ch. 1.4 - In Problems 31-42:
(a) Find the domain of each...Ch. 1.4 - In Problems 31-42: (a) Find the domain of each...Ch. 1.4 - In Problems 31-42: (a) Find the domain of each...Ch. 1.4 - In Problems 31-42: (a) Find the domain of each...Ch. 1.4 - In Problems 31-42:
(a) Find the domain of each...Ch. 1.4 - In Problems 31-42: (a) Find the domain of each...Ch. 1.4 - In Problems 31-42:
(a) Find the domain of each...Ch. 1.4 - In Problems 31-42:
(a) Find the domain of each...Ch. 1.4 - In Problems 31-42:
(a) Find the domain of each...Ch. 1.4 -
Find the domain of the function.
Locate any...Ch. 1.4 - Prob. 42AYUCh. 1.4 - In Problems 43-46, the graph of a...Ch. 1.4 - In Problems 43-46, the graph of a...Ch. 1.4 - In Problems 43-46, the graph of a...Ch. 1.4 - In Problems 43-46, the graph of a...Ch. 1.4 - If f( x )=int( 2x ) , find (a) f( 1.2 ) (b) f( 1.6...Ch. 1.4 - 48. If , find
(a) (b) (c)
Ch. 1.4 - Graph f(x)={(x1)2if0x22x+10if2x6 Find the domain...Ch. 1.4 - Graph f(x)={x+1if2x02ifx=0x+1if0x2 Find the domain...Ch. 1.4 -
51. Tablet Service A monthly tablet plan costs...Ch. 1.4 - Parking at OHare International Airport The...Ch. 1.4 - Cost of Natural Gas In March , Laclede Gas had the...Ch. 1.4 - Cost of Natural Gas In March , Nicor Gas had the...Ch. 1.4 - Federal Income Tax Two 2017 Tax Rate Schedules are...Ch. 1.4 - Federal Income Tax Refer to the 2018 tax rate...Ch. 1.4 - 57. Cost of Transporting Goods A trucking company...Ch. 1.4 - Car Rental Costs An economy car rented in Florida...Ch. 1.4 - Mortgage Fees Fannie Mae charges a loan-level...Ch. 1.4 - Minimum Payments for Credit Cards Holders of a...Ch. 1.4 - Wind Chill The wind chill factor represents the...Ch. 1.4 - Wind Chill Redo Problem 61(a)-(d) for an air...Ch. 1.4 - Wind Chill First-class Mail In 2015 the U.S....Ch. 1.4 - In Problems 64-71, use a graphing utility....Ch. 1.4 - In Problems 64-71, use a graphing utility....Ch. 1.4 - Exploration Graph . Then on the same screen graph...Ch. 1.4 - In Problems 64-71, use a graphing utility....Ch. 1.4 - In Problems 64-71, use a graphing utility.
68....Ch. 1.4 - In Problems 64-71, use a graphing utility....Ch. 1.4 - In Problems 64-71, use a graphing utility....Ch. 1.4 - In Problems 64-71, use a graphing utility....Ch. 1.4 - In Problems 64-71, use a graphing utility.
72....Ch. 1.4 - In Problems 64-71, use a graphing utility.
73....Ch. 1.5 - 1. Suppose that the graph of a function f is...Ch. 1.5 - Suppose that the graph of a function f is known....Ch. 1.5 - 3. True or False The graph of is the graph of ...Ch. 1.5 - 4. True or False The graph of is the reflection...Ch. 1.5 - Which of the following functions has a graph that...Ch. 1.5 - 6. Which of the following functions has a graph...Ch. 1.5 - In problems 7-18, match each graph to one of the...Ch. 1.5 - In problems 7-18, match each graph to one of the...Ch. 1.5 - In problems 7-18, match each graph to one of the...Ch. 1.5 - In problems 7-18, match each graph to one of the...Ch. 1.5 - In problems 7-18, match each graph to one of the...Ch. 1.5 - In problems 7-18, match each graph to one of the...Ch. 1.5 - In problems 7-18, match each graph to one of the...Ch. 1.5 - In problems 7-18, match each graph to one of the...Ch. 1.5 - In problems 7-18, match each graph to one of the...Ch. 1.5 - In problems 7-18, match each graph to one of the...Ch. 1.5 - In problems 7-18, match each graph to one of the...Ch. 1.5 - In problems 7-18, match each graph to one of the...Ch. 1.5 - In Problem 19-26, write the function whose graph...Ch. 1.5 - In Problem 19-26, write the function whose graph...Ch. 1.5 - In Problem 19-26, write the function whose graph...Ch. 1.5 - In Problem 19-26, write the function whose graph...Ch. 1.5 - In Problem 19-26, write the function whose graph...Ch. 1.5 - In Problem 19-26, write the function whose graph...Ch. 1.5 - In Problems 1928, write the function whose graph...Ch. 1.5 - In Problem 19-26, write the function whose graph...Ch. 1.5 - In Problem 27-30, find the function that is...Ch. 1.5 - In Problem 27-30, find the function that is...Ch. 1.5 - In problem 27-30, find the function that is...Ch. 1.5 - In Problem 27-30, find the function that is...Ch. 1.5 - In Problem 27-30, find the function that is...Ch. 1.5 - In Problem 27-30, find the function that is...Ch. 1.5 - In Problem 27-30, find the function that is...Ch. 1.5 - In Problem 27-30, find the function that is...Ch. 1.5 - Suppose that the x-intercepts of the graph of...Ch. 1.5 - Suppose that the x-intercepts of the graph of...Ch. 1.5 - 37. Suppose that the function is increasing on...Ch. 1.5 - 38. Suppose that the function is increasing on...Ch. 1.5 - In Problems 39-62, graph each function using the...Ch. 1.5 - In Problems 39-62, graph each function using the...Ch. 1.5 - In problem 39-62, graph each function using the...Ch. 1.5 - In problem 39-62, graph each function using the...Ch. 1.5 - In Problems 39-62, graph each function using the...Ch. 1.5 - In Problems 39-62, graph each function using the...Ch. 1.5 - In problem 39-62, graph each function using the...Ch. 1.5 - In Problems 39-62, graph each function using the...Ch. 1.5 - In Problems 39-62, graph each function using the...Ch. 1.5 - In Problems 39-62, graph each function using the...Ch. 1.5 - In Problems 39-62, graph each function using the...Ch. 1.5 - In Problems 39-62, graph each function using the...Ch. 1.5 - In Problems 39-62, graph each function using the...Ch. 1.5 - In Problems 39-62, graph each function using the...Ch. 1.5 - In Problems 39-62, graph each function using the...Ch. 1.5 - In Problems 39-62, graph each function using the...Ch. 1.5 - In Problems 39-62, graph each function using the...Ch. 1.5 - In Problems 39-62, graph each function using the...Ch. 1.5 - In Problems 39-62, graph each function using the...Ch. 1.5 - In Problems 39-62, graph each function using the...Ch. 1.5 - In Problems 39-62, graph each function using the...Ch. 1.5 - In Problems 39-62, graph each function using the...Ch. 1.5 - In Problems 39-62, graph each function using the...Ch. 1.5 - In Problems 39-62, graph each function using the...Ch. 1.5 - In Problems 63-66, the graph of a function f is...Ch. 1.5 - In Problems 63-66, the graph of a function f is...Ch. 1.5 - In Problems 63-66, the graph of a function f is...Ch. 1.5 - In Problems 63-66, the graph of a function f is...Ch. 1.5 - In Problems 69-76, complete the square of each...Ch. 1.5 - In Problems 69-76, complete the square of each...Ch. 1.5 - In Problems 69-76, complete the square of each...Ch. 1.5 - In Problems 69-76, complete the square of each...Ch. 1.5 - Prob. 71AYUCh. 1.5 - In Problems 69-76, complete the square of each...Ch. 1.5 - In Problems 69-76, complete the square of each...Ch. 1.5 - In Problems 69-76, complete the square of each...Ch. 1.5 - 77. The graph of a function f is illustrated in...Ch. 1.5 - 78. The graph of a function f is illustrated in...Ch. 1.5 - 79. Suppose ( 1,3 ) is a point on the graph of...Ch. 1.5 - 80. Suppose is a point on the graph of .
(a) What...Ch. 1.5 - 81. Graph the following functions using...Ch. 1.5 - 82. Graph the following functions using...Ch. 1.5 - 83. (a) Graph using transformations.
(b) Find...Ch. 1.5 - 84. (a) Graph using transformations.
(b) Find...Ch. 1.5 - 85. Thermostat Control Energy conservation experts...Ch. 1.5 - Digital Music Revenues The total projected...Ch. 1.5 - 87. Temperature Measurements The relationship...Ch. 1.5 - 88. Period of a Pendulum The period T (in seconds)...Ch. 1.5 - 89. The equation y= ( xc ) 2 defines a family of...Ch. 1.5 - 90. Repeat Problem 89 for the family of parabolas...Ch. 1.5 - 91. Suppose that the graph of a function f is...Ch. 1.5 - 92. Suppose that the graph of a function f is...Ch. 1.5 - 93. The area under the curve y= x bounded front...Ch. 1.5 - 94. Explain how the range of the function compares...Ch. 1.5 - 95. Explain how the domain of compares to the...Ch. 1.6 - 1. Let be a point on the graph of .
(a) ...Ch. 1.6 - 2. Let be a point on the graph of.
(a) ...Ch. 1.6 - 3. P=( x,y ) be a point on the graph of y= x . (a)...Ch. 1.6 - Let P=(x,y) be a point on the graph of y=1x....Ch. 1.6 - 5. A right triangle has one vertex on the graph of...Ch. 1.6 - 5. A right triangle has one vertex on the graph of...Ch. 1.6 - 7. A rectangle has one corner in quadrant I on the...Ch. 1.6 - A rectangle is inscribed in a semicircle of radius...Ch. 1.6 - 9. A rectangle is inscribed in a circle of radius...Ch. 1.6 - 10. A circle of radius r is inscribed in a square....Ch. 1.6 - 11. Geometry A wire 10 meters long is to be cut...Ch. 1.6 - Prob. 12AYUCh. 1.6 - 13. Geometry A wire of length x is bent into the...Ch. 1.6 - Prob. 14AYUCh. 1.6 - 15. Geometry A semicircle of radius r is inscribed...Ch. 1.6 - 16. Geometry An equilateral triangle is inscribed...Ch. 1.6 - 17. Geometry An equilateral triangle is inscribed...Ch. 1.6 - 18. Uniform Motion Two cars leave an intersection...Ch. 1.6 - 19. Uniform Motion Two cars are approaching an...Ch. 1.6 - 20. Inscribing a Cylinder in a Sphere Inscribe a...Ch. 1.6 - 21. Inscribing a Cylinder in a Cone Inscribe a...Ch. 1.6 - 22. Installing Cable TV MetroMedia Cable is asked...Ch. 1.6 - 23. Time Required to Go from an Island to a Town...Ch. 1.6 - Filling a Conical Tank Water is poured into a...Ch. 1.6 - Constructing an Open Box An open box with a square...Ch. 1.6 - 26. Constructing an Open Box An open box with a...Ch. 1.7 - 1. If x and y are two quantities, then y is...Ch. 1.7 - True or False If y varies directly with x, then y...Ch. 1.7 - Which equation represents a joints variation...Ch. 1.7 - Choose the best description for the model , if is...Ch. 1.7 - In Problems 5-16, write a general formula to...Ch. 1.7 - In Problems 5 – 16, write a general formula to...Ch. 1.7 - In Problems 5 16, write a general formula to...Ch. 1.7 - In Problems 5 – 16, write a general formula to...Ch. 1.7 - In Problems 5 – 16, write a general formula to...Ch. 1.7 - In Problems 5 – 16, write a general formula to...Ch. 1.7 - In Problems 5 16, write a general formula to...Ch. 1.7 - In Problems 5 16, write a general formula to...Ch. 1.7 - In Problems 5 16, write a general formula to...Ch. 1.7 - In Problems 5 16, write a general formula to...Ch. 1.7 - In Problems 5 – 16, write a general formula to...Ch. 1.7 - In Problems 5 16, write a general formula to...Ch. 1.7 - In Problems 17 22, write an equation that relates...Ch. 1.7 - In Problems 17 – 22, write an equation that...Ch. 1.7 - In Problems 17 – 22, write an equation that...Ch. 1.7 - In Problems 17 22, write an equation that relates...Ch. 1.7 - In Problems 17 – 22, write an equation that...Ch. 1.7 - In Problems 17 22, write an equation that relates...Ch. 1.7 - Mortgage Payments The monthly payment p on a...Ch. 1.7 - 24. Mortgage Payments The monthly payment p on a...Ch. 1.7 - 25. Physics: Falling Objects The distance s that...Ch. 1.7 - 26. Physics: Falling Objects The velocity v is a...Ch. 1.7 - Physics: stretching a Spring The elongation E of a...Ch. 1.7 - Physics: Vibrating String The rate of vibration of...Ch. 1.7 - Revenue Equation At the corner Shell station, the...Ch. 1.7 - Cost Equation The cost C of roasted almonds varies...Ch. 1.7 - Demand Suppose that the demand D for candy at the...Ch. 1.7 - 32. Driving to School The time t that it takes to...Ch. 1.7 - Pressure The volume of gas V held at a constant...Ch. 1.7 - Resistance The current i in a circuit is inversely...Ch. 1.7 - Weight The weight of an object above the surface...Ch. 1.7 - 36. Weight of a body: The weight of a body above...Ch. 1.7 - Geometry The volume V of a right circular cylinder...Ch. 1.7 - Geometry The volume V of a right circular cone...Ch. 1.7 - Intensity of Light The intensity I of light (...Ch. 1.7 - Force of the Wind on a Window The force exerted by...Ch. 1.7 - Prob. 41AYUCh. 1.7 - Chemistry: Gas Laws The volume V of an ideal gas...Ch. 1.7 - Physics Kinetic Energy The kinetic energy K of a...Ch. 1.7 - Electrical Resistance of a Wire The electrical...Ch. 1.7 - Measuring the Stress of Materials The stress in...Ch. 1.7 - 46. Safe Loan for a Beam The maximum safe load for...Ch. 1.7 - 47. In the early 17th century, Johannes Kepler...Ch. 1.7 - Using a situation that has not been discussed in...Ch. 1.7 - Using a situation that has not been discussed in...Ch. 1.7 - 50. Using a situation that has not been discussed...Ch. 1 - In Problems 1 and 2, determine whether each...Ch. 1 - In Problems 1 and 2, determine whether each...Ch. 1 - In Problems 3-5, find the following for each...Ch. 1 - In Problems 3-5, find the following for each...Ch. 1 - In Problems 3-5, find the following for each...Ch. 1 - Prob. 6RECh. 1 - Prob. 7RECh. 1 - In Problems 6-11, find the domain of each...Ch. 1 - In Problems 6-11, find the domain of each...Ch. 1 - In Problems 6-11, find the domain of each...Ch. 1 - In Problems 6-11, find the domain of each...Ch. 1 - In Problems 12-14, find f+g,fg,fg,and f g for each...Ch. 1 - In Problems 12-14, find f+g,fg,fg,and f g for each...Ch. 1 - Prob. 14RECh. 1 - Find the difference quotient of f( x )=2 x 2 +x+1...Ch. 1 - Consider the graph of the function f on the right....Ch. 1 - Prob. 17RECh. 1 - Prob. 18RECh. 1 - Prob. 19RECh. 1 - Prob. 20RECh. 1 - In Problems 18-21, determine (algebraically)...Ch. 1 - In problems 25 and 26, use a graphing utility to...Ch. 1 - In problems 25 and 26, use a graphing utility to...Ch. 1 - Find the average rate of change of f( x )=8 x 2 x...Ch. 1 - In Problems 25 and 26, find the average rate of...Ch. 1 - In Problems 25 and 26, find the average rate of...Ch. 1 - In Problems 27 and 28, is the graph shown the...Ch. 1 - In Problems 27 and 28, is the graph shown the...Ch. 1 - In Problems 29 and 30, graph each function. Be...Ch. 1 - In Problems 29 and 30, graph each function. Be...Ch. 1 - Prob. 31RECh. 1 - Prob. 32RECh. 1 - Prob. 33RECh. 1 - Prob. 34RECh. 1 - Prob. 35RECh. 1 - Prob. 36RECh. 1 - In Problems 37 and 38: (a) Find the domain of each...Ch. 1 - In Problems 37 and 38: (a) Find the domain of each...Ch. 1 - A function f is defined by f( x )= Ax+5 6x2 If f(...Ch. 1 - Constructing a Closed Box A closed box with a...Ch. 1 - Area of a Rectangle A rectangle has one vertex in...Ch. 1 - Mortgage Payments The monthly payment p on a...Ch. 1 - Prob. 43RECh. 1 - Prob. 44RECh. 1 - Find the domain and range of each relation. Then...Ch. 1 - In Problems 24, find the domain of each function...Ch. 1 - In Problems 24, find the domain of each function...Ch. 1 - In Problems 24, find the domain of each function...Ch. 1 - Consider the graph of the function f below. Find...Ch. 1 - Graph the function f(x)=x4+2x3+4x22 on the...Ch. 1 - Consider the function g(x)={2x+1ifx1x4ifx1 Graph...Ch. 1 - 8. For the function, find the average rate of...Ch. 1 - 9. For the functionand, find the following and...Ch. 1 - Graph each function using the techniques of...Ch. 1 - The variable interest rate on a student loan...Ch. 1 - A community skating rink is in the shape of a...Ch. 1 - The resistance (in ohms) of a circular conductor...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- Given ƒ = (10, -10) and q = (-8, −7), find ||ƒ— q|| and dƒ-9. Give EXACT answers. You do NOT have to simplify your radicals!arrow_forwardFind a vector (u) with magnitude 7 in the direction of v = (2,4) Give EXACT answer. You do NOT have to simplify your radicals!arrow_forwardGiven g = (-5, 10) and u = (5, 2), find -4ğ - 6.arrow_forward
- Given the vector v→=⟨3,-5⟩, find the magnitude and angle in which the vector points (measured in radians counterclockwise from the positive x-axis and 0≤θ<2π). Round each decimal number to two places.arrow_forwardplease include radicals in answerarrow_forwardFind the arc length of the curve below on the given interval by integrating with respect to x. 4 4 + 1 8x 2 [1,3]arrow_forward
- Given that the outward flux of a vector field through the sphere of radius r centered at the origin is 5(1 cos(2r)) sin(r), and D is the value of the divergence of the vector field at the origin, the value of sin (2D) is -0.998 0.616 0.963 0.486 0.835 -0.070 -0.668 -0.129arrow_forward10 The hypotenuse of a right triangle has one end at the origin and one end on the curve y = Express the area of the triangle as a function of x. A(x) =arrow_forwardIn Problems 17-26, solve the initial value problem. 17. dy = (1+ y²) tan x, y(0) = √√3arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
01 - What Is A Differential Equation in Calculus? Learn to Solve Ordinary Differential Equations.; Author: Math and Science;https://www.youtube.com/watch?v=K80YEHQpx9g;License: Standard YouTube License, CC-BY
Higher Order Differential Equation with constant coefficient (GATE) (Part 1) l GATE 2018; Author: GATE Lectures by Dishank;https://www.youtube.com/watch?v=ODxP7BbqAjA;License: Standard YouTube License, CC-BY
Solution of Differential Equations and Initial Value Problems; Author: Jefril Amboy;https://www.youtube.com/watch?v=Q68sk7XS-dc;License: Standard YouTube License, CC-BY