
To find:
a) The
b) The suitable indicator for the titration referring figure 16.5
c) The
d) Sketch the titration curve
Answer to Problem 16.126QA
Solution:
a) The calculated
b) The suitable indicator for the titration, referring figure 16.5, is Alizarin Yellow R.
c) The
1)
2)
3)
4)
5)
6)
7)
8)
9)
10)
11)
12)
13)
14)
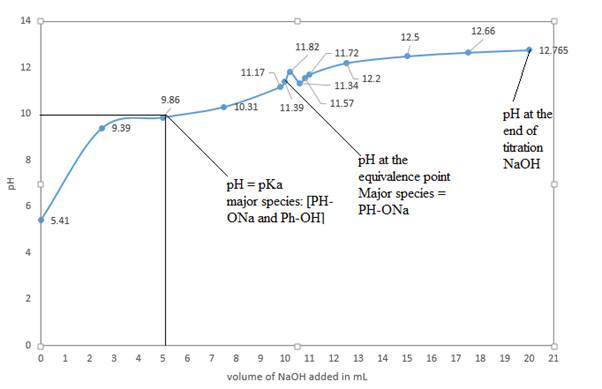
d) In the sketched titration curve
The major species at the equivalence point is
The major species at the end of titration is
Explanation of Solution
1) Concept:
To calculate the pH of a weak acid with a strong base, we need to use reaction stoichiometry and RICE table. First, we will calculate the equivalence point from the volume and molarity of base and acid. We will calculate the pH at equivalence point by using the RICE table. At the equivalence point, moles of phenol and
2) Formulae:
i)
ii)
iii)
iv)
3) Given:
i) Volume of phenol =
ii) Molarity of phenol
iii)
iv) Molarity of
4) Calculations:
a) Calculating
Step 1)
Finding the volume of
At the equivalence point, moles of phenol = moles of
At the equivalence point, moles of phenol and
Calculating the volume of
So, at the equivalence point, the volume of
So, the total volume of solution is
At the equivalence point, sodium salt of phenol is formed, and its moles will be equal to moles of phenol and
Calculating the molarity of sodium phenoxide:
Step 2)
Creating an RICE table for the dissociation of sodium phenoxide
| RICE | |||
| Initial (M) | |||
| Change (M) | |||
| Equilibrium (M) | |||
Writing the
The calculated
b) Choosing the indicator, which is suitable for the titration referring to figure 16.5:
A
c) Calculating the
The calculated volume of
1) Addition of 0.0 mL NaOH:
At 0.0mL NaOH added, the
| RICE | |||
| Initial (M) | |||
| Change (M) | |||
| Equilibrium (M) | |||
So, the
2) Addition of 2.5 mL NaOH:
Moles of phenol:
Moles of
We create a modified RICE table to determine how many moles of acid remain and how many moles of conjugate base have been produced:
| Initial (mol) | |||
| Change (mol) | |||
| Final (mol) | |||
The total sample volume is
Applying the Henderson-Hasselbalch equation for the above buffer system formed as
3) Addition of 5.0 mL NaOH:
Moles of phenol:
Moles of
We create a modified RICE table to determine how many moles of acid remain and how many moles of conjugate base have been produced:
| Initial (mol) | |||
| Change (mol) | |||
| Final (mol) | |||
The total sample volume is
Applying the Henderson-Hasselbalch equation for the above buffer system formed as
4) Addition of 7.5 mL NaOH:
Moles of phenol:
Moles of
We create a modified RICE table to determine how many moles of acid remains and how many moles of conjugate base have been produced.
| Initial (mol) | |||
| Change (mol) | |||
| Final (mol) | |||
The total sample volume is
Applying the Henderson-Hasselbalch equation for the above buffer system formed as
5) Addition of 9.8 mL NaOH:
Moles of phenol:
Moles of
We create a modified RICE table to determine how many moles of acid remain and how many moles of conjugate base have been produced:
| Initial (mol) | |||
| Change (mol) | |||
| Final (mol) | |||
The total sample volume is
Applying the Henderson-Hasselbalch equation for the above buffer system formed as
6) Addition of 10 mL NaOH:
Moles of phenol:
Moles of
We create a modified RICE table to determine how many moles of acid remain and how many moles of conjugate base have been produced:
| Initial (mol) | |||
| Change (mol) | |||
| Final (mol) | |||
The total sample volume is
Applying the Henderson-Hasselbalch equation for the above buffer system formed as
7) Addition of 10.2 mL NaOH:
Moles of phenol:
Moles of
We create a modified RICE table to determine how many moles of acid remain and how many moles of conjugate base have been produced:
| Initial (mol) | |||
| Change (mol) | |||
| Final (mol) | |||
The total sample volume is
Applying the Henderson-Hasselbalch equation for the above buffer system formed as
8) Addition of 10.6 mL NaOH:
The contribution of
Moles of
| Initial (mol) | |||
| Change (mol) | |||
| Final (mol) | |||
Total volume of solution =
Molarity of
9) Addition of 10.8 mL NaOH
Moles of
| Initial (mol) | |||
| Change (mol) | |||
| Final (mol) | |||
Total volume of solution =
Molarity of
10) Addition of 11 mL NaOH
Moles of
| Initial (mol) | |||
| Change (mol) | |||
| Final (mol) | |||
Total volume of solution =
Molarity of
11) Addition of 12.5 mL NaOH
Moles of
| Initial (mol) | |||
| Change (mol) | |||
| Final (mol) | |||
Total volume of solution =
Molarity of
12) Addition of 15 mL NaOH
Moles of
| Initial (mol) | |||
| Change (mol) | |||
| Final (mol) | |||
Total volume of solution =
Molarity of
13) Addition of 17.5 mL NaOH:
Moles of
| Initial (mol) | |||
| Change (mol) | |||
| Final (mol) | |||
Total volume of solution =
Molarity of
14) Addition of
Moles of
| Initial (mol) | |||
| Change (mol) | |||
| Final (mol) | |||
Total volume of solution =
Molarity of
d) Graph of

The above curve is a plot of
The volume of
So, at half equivalence point, the major species would be
At the equivalence point, moles of acid initially present are equal to moles of added base. So, there will not be phenol or
At the end of the titration, the only major species present will be
Conclusion:
In the titration of a weak acid and strong base, the resultant salt formed is a basic salt. Hence, the
Want to see more full solutions like this?
Chapter 16 Solutions
Chemistry: An Atoms-Focused Approach (Second Edition)
- Draw the Zaitsev product of the dehydration of this alcohol. + I X 5 OH ざ~ TSOH Click and drag to start drawing a structure.arrow_forwardPlease help with identifying these.arrow_forwardFor the reaction: CO2(g) + H2(g) --> CO (g) + H2O (g) Kc= 0.64 at 900 degrees celcius. if initially you start with 1.00 atmoshpere of carbon dioxide and 1 atmoshpere of hydrogen gas, what are the equilibrium partial pressuses of all species.arrow_forward
- Can I please get this answered? With the correct number of significant digits.arrow_forwardDraw the Hofmann product of the dehydroiodination of this alkyl iodide. ☐ : + Explanation Check esc F1 2 3 I 88 % 5 F5 I. X © tBuOK Click and drag to sta drawing a structure. © 2025 McGraw Hill LLC. All Rights Reserved. Te BI BB F6 W E R Y S H Karrow_forwardCan I please get help with this graph, if you could show exactly where it needs to pass through please.arrow_forward
- Draw the condensed structure of 1,3-dihydroxy-2-pentanone. Explanation Check Click anywhere to draw the first atom of your structure. Х C © 2025 McGraw Hill LLC. All Rights Reserved. Terms of use +arrow_forward0.500 moles of NOCl are placed into a 1.00 L vessesl at 700K and after the system comes to equilibrium, the consentration of NOCl is 0.440 M. Calculate the equilibrium constant Kc for the reaction: 2NOCL (g) --> 2NO (g) + Cl2 (g)arrow_forwardWhat is the hydronium ion concentration in a solution of water that has a hydroxide ion concentrationof 1.0 x 10-2 M?arrow_forward
 ChemistryChemistryISBN:9781305957404Author:Steven S. Zumdahl, Susan A. Zumdahl, Donald J. DeCostePublisher:Cengage Learning
ChemistryChemistryISBN:9781305957404Author:Steven S. Zumdahl, Susan A. Zumdahl, Donald J. DeCostePublisher:Cengage Learning ChemistryChemistryISBN:9781259911156Author:Raymond Chang Dr., Jason Overby ProfessorPublisher:McGraw-Hill Education
ChemistryChemistryISBN:9781259911156Author:Raymond Chang Dr., Jason Overby ProfessorPublisher:McGraw-Hill Education Principles of Instrumental AnalysisChemistryISBN:9781305577213Author:Douglas A. Skoog, F. James Holler, Stanley R. CrouchPublisher:Cengage Learning
Principles of Instrumental AnalysisChemistryISBN:9781305577213Author:Douglas A. Skoog, F. James Holler, Stanley R. CrouchPublisher:Cengage Learning Organic ChemistryChemistryISBN:9780078021558Author:Janice Gorzynski Smith Dr.Publisher:McGraw-Hill Education
Organic ChemistryChemistryISBN:9780078021558Author:Janice Gorzynski Smith Dr.Publisher:McGraw-Hill Education Chemistry: Principles and ReactionsChemistryISBN:9781305079373Author:William L. Masterton, Cecile N. HurleyPublisher:Cengage Learning
Chemistry: Principles and ReactionsChemistryISBN:9781305079373Author:William L. Masterton, Cecile N. HurleyPublisher:Cengage Learning Elementary Principles of Chemical Processes, Bind...ChemistryISBN:9781118431221Author:Richard M. Felder, Ronald W. Rousseau, Lisa G. BullardPublisher:WILEY
Elementary Principles of Chemical Processes, Bind...ChemistryISBN:9781118431221Author:Richard M. Felder, Ronald W. Rousseau, Lisa G. BullardPublisher:WILEY





