EBK MATHEMATICS FOR ELEMENTARY TEACHERS
5th Edition
ISBN: 9780134506609
Author: Beckmann
Publisher: PEARSON CUSTOM PUB.(CONSIGNMENT)
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 15.2, Problem 3P
Table 15.3 shows women’s 400-meter freestyle Olympic winning times in recent history.
a. Make a graphical display of the data in Table 15.3.
b. Write at least four questions about your graph in part (a); include at least one at each of the three graph-reading levels. Label each question with its level. Answer your questions (to the extent that it is possible) and explain your answers briefly.
Table 15.3 Women’s 400-meter freestyle Olympic winningtimes.
Source: Qlympic.org, Official Website of the Olympic Movement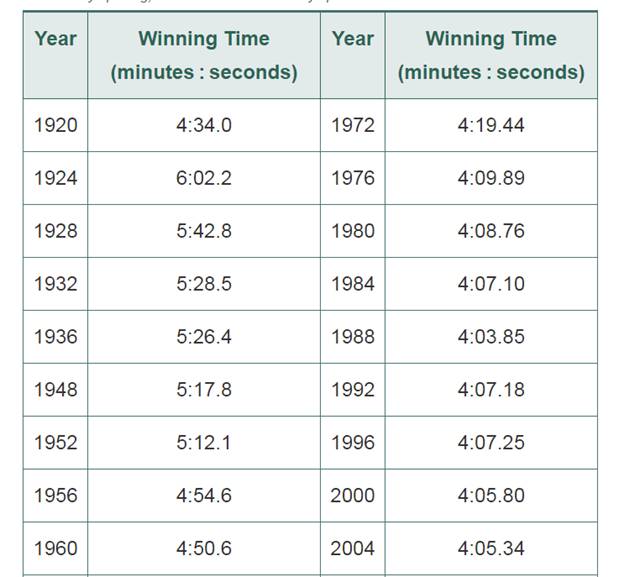
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Refer to page 90 for a problem requiring Fourier series expansion of a given periodic function.
Instructions: Clearly outline the process of finding Fourier coefficients. Provide all calculations,
integrals, and final expansions.
Link: [https://drive.google.com/file/d/1wKSrun-GlxirS31Z9qoHazb9tC440 AZF/view?usp=sharing]
Refer to page 93 for a problem involving Cauchy-Euler differential equations.
Instructions: Solve the given differential equation step-by-step, showing the characteristic roots
and general solution clearly.
Refer to page 80 for a proof of convergence for a given series using the ratio test.
Instructions: Clearly apply the ratio test. Show all steps and provide justification for convergence
or divergence.
Link: [https://drive.google.com/file/d/1wKSrun-GlxirS3IZ9qoHazb9tC440 AZF/view?usp=sharing]
Refer to page 94 for a problem requiring the numerical solution of an ODE using the Runge-
Kutta method.
Instructions: Solve step-by-step, showing iterations, step sizes, and calculations clearly.
Link: [https://drive.google.com/file/d/1wKSrun-GlxirS3IZ9qo Hazb9tC440AZF/view?usp=sharing]
Refer to page 82 for a double integral problem. Convert the integral into polar coordinates and
evaluate it step-by-step, clearly showing all transformations and limits.
Instructions: Focus only on the problem. Provide all steps, including the coordinate
transformation, Jacobian factor, and the integral evaluation. Avoid irrelevant details.
Link: [https://drive.google.com/file/d/1wKSrun-GlxirS31Z9qoHazb9tC440 AZF/view?usp=sharing]
Chapter 15 Solutions
EBK MATHEMATICS FOR ELEMENTARY TEACHERS
Ch. 15.1 - Give two examples of a statistical question and...Ch. 15.1 - A class has a collection of 100 bottle caps and...Ch. 15.1 - Neil, a third-grader, asked 10 of his classmates...Ch. 15.1 - An announcer of a TV program invited viewers to...Ch. 15.1 - There is a bowl containing 300 plastic tiles. Some...Ch. 15.1 - There is a bowl containing 80 green tiles and an...Ch. 15.1 - At a factory that produces doorknobs, 1500...Ch. 15.1 - At a factory that produces switches, 3000 switches...Ch. 15.1 - At a light bulb factory, 1728 light bulbs are...Ch. 15.1 - Carter has a large collection of marbles. He knows...
Ch. 15.1 - The following problem is an example of the...Ch. 15.1 - A group studying violence wants to determine the...Ch. 15.2 - Three third-grade classes are having a contest to...Ch. 15.2 - Find 3 coins of any type (as long as all 3 have a...Ch. 15.2 - Table 15.3 shows women’s 400-meter freestyle...Ch. 15.2 - Using an Internet browser, go to census.gov, the...Ch. 15.2 - Using an Internet browser, go to the webpage of...Ch. 15.2 - Using an Internet browser, go to one of the...Ch. 15.2 - Using an Internet browser, go to one of the...Ch. 15.2 - a. Describe in detail an activity suitable for use...Ch. 15.3 - In your own words, explain why the following two...Ch. 15.3 - Explain why the mean of a list of numbers must...Ch. 15.3 - Explain why the mean of two numbers is exactly...Ch. 15.3 - Shante caught 17 ladybugs every day for 4 days....Ch. 15.3 - John’s average annual income over a 4-year period...Ch. 15.3 - Tracy’s times swimming 200 yards were as follows:...Ch. 15.3 - Explain how you can quickly calculate the mean of...Ch. 15.3 - Explain how you can quickly calculate the mean of...Ch. 15.3 - average on her first 3 math tests was 80. Her...Ch. 15.3 - A teacher gives a 10-point test to a class of 10...Ch. 15.3 - In your own words, describe how to view the mean...Ch. 15.3 - Discuss Jessica’s reasoning about calculating the...Ch. 15.3 - ]The dot plot in Figure 15.21 represents the...Ch. 15.3 - For each of the following situations, decide...Ch. 15.3 - A teacher gives a 10-point test to a class of 9...Ch. 15.3 - A teacher gives a 10-point test to a class of 9...Ch. 15.3 - In Ritzy County, the average annual household...Ch. 15.3 - In county A, the average score on the grade 5 Iowa...Ch. 15.3 - a. The histogram at the top of Figure 15.22 shows...Ch. 15.3 - * Ms. Smith needs to figure her students’ homework...Ch. 15.3 - The average speed of a moving object during a...Ch. 15.4 - What is the difference between scoring in the 90th...Ch. 15.4 - What is the purpose of reporting a student’s...Ch. 15.4 - The three histograms in Figure 15.37 show the...Ch. 15.4 - At a math center in a class, there is a bag filled...Ch. 15.4 - Refer to Figure 15.26 on page 706. a. Refer to the...Ch. 15.4 - Refer to Figure 15.26 on page 706. a. Refer to the...Ch. 15.4 - Refer to Figure 15.26 on page 706. a. Write at...Ch. 15.4 - Use the NAEP long-term trend data about...Ch. 15.4 - Determine the median and interquartile range for...Ch. 15.4 - a. Make a box plot for the data in Figure 15.38....Ch. 15.4 - Determine the medians and interquartile ranges for...Ch. 15.4 - a. Make box plots for the dot plots in Figure...Ch. 15.4 - A fifth-grade class is wondering ¡f girls’ names...Ch. 15.4 - Compute the mean and the MAD for each of the dot...Ch. 15.4 - On a state-wide test graded on a 10-point scale,...Ch. 15.4 - A 400-point test is given to a group of students....
Additional Math Textbook Solutions
Find more solutions based on key concepts
1. How much money is Joe earning when he’s 30?
Pathways To Math Literacy (looseleaf)
Find all solutions of each equation in the interval .
Precalculus: A Unit Circle Approach (3rd Edition)
Is there a relationship between wine consumption and deaths from heart disease? The table gives data from 19 de...
College Algebra Essentials (5th Edition)
For Problems 23-28, write in simpler form, as in Example 4. logbFG
Finite Mathematics for Business, Economics, Life Sciences and Social Sciences
First Derivative Test a. Locale the critical points of f. b. Use the First Derivative Test to locale the local ...
Calculus: Early Transcendentals (2nd Edition)
Find how many SDs above the mean price would be predicted to cost.
Intro Stats, Books a la Carte Edition (5th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- Refer to page 81 for a proof involving the uniqueness of solutions for a given ordinary differential equation. Instructions: Focus strictly on proving the uniqueness theorem using necessary conditions. Justify all intermediate steps. Link: [https://drive.google.com/file/d/1wKSrun-GlxirS31Z9qoHazb9tC440AZF/view?usp=sharing]arrow_forwardRefer to page 88 for a problem on solving a Laplace equation in polar coordinates with boundary conditions. Instructions: Solve step-by-step using separation of variables. Clearly show transformations and solutions. Avoid irrelevant details. Link: [https://drive.google.com/file/d/1wKSrun-GlxirS3IZ9qoHazb9tC440AZF/view?usp=sharing]arrow_forwardRefer to page 89 for a line integral problem. Apply Green's Theorem to convert the line integral into a double integral. Solve it step-by-step, showing all calculations and transformations. Instructions: Outline the problem clearly. Focus on applying Green's Theorem correctly and show all double integral calculations. Avoid irrelevant content. Link [https://drive.google.com/file/d/1wKSrun-GlxirS31Z9qoHazb9tC440 AZF/view?usp=sharing]arrow_forward
- On page 85, a power series is given. Use the root test to prove its convergence or divergence and determine its radius of convergence. Instructions: Solve step-by-step. Apply the root test rigorously, and show all intermediate calculations. Avoid irrelevant details. Link: [https://drive.google.com/file/d/1wKSrun-GlxirS3IZ9qoHazb9tC440AZF/view?usp=sharing]arrow_forwardRefer to page 77 for a problem requiring the Taylor series expansion of a function about a given point. Derive the series up to the specified order, showing all intermediate steps. Instructions: Focus on deriving the Taylor series. Clearly outline all steps, including finding derivatives and substituting into the series formula. Show detailed calculations. Link: [https://drive.google.com/file/d/1wKSrun-GlxirS31Z9qo Hazb9tC440 AZ F/view?usp=sharing]arrow_forwardRefer to page 81 for a proof of the Cauchy-Schwarz inequality in vector spaces. Provide a detailed, step-by-step proof, including all intermediate reasoning. Instructions: Focus strictly on proving the inequality. Clearly outline each step and justify all intermediate results. Irrelevant content is not accepted. Link: [https://drive.google.com/file/d/1wKSrun-GlxirS3IZ9qoHazb9tC440AZF/view?usp=sharing]arrow_forward
- On page 89, there is an initial value problem (IVP) for an ordinary differential equation. Solve the IVP using the Laplace Transform method. Instructions: Solve step-by-step using Laplace Transforms. Show all transformations, algebraic manipulations, and the final inverse transform with clear calculations. Irrelevant explanations are not allowed. Link: [https://drive.google.com/file/d/1wKSrun-GlxirS3IZ9qo Hazb9tC440 AZF/view?usp=sharing]arrow_forwardOn page 98, an eigenvalue problem for a differential operator is provided. Solve for the eigenvalues and eigenfunctions using boundary conditions. Instructions: Stick to solving the problem. Provide step-by-step calculations for determining eigenvalues and corresponding eigenfunctions. Avoid irrelevant details. Link: [https://drive.google.com/file/d/1wKSrun-GlxirS3IZ9qoHazb9tC440AZF/view?usp=sharing]arrow_forwardRefer to page 70 for a non-exact differential equation. Solve the equation by finding a suitable integrating factor. Verify the exactness after applying the factor and determine the solution step-by-step. Instructions: Provide only relevant content. Solve step-by-step, clearly showing how the integrating factor is found and applied. All calculations must be detailed and correct. Link: [https://drive.google.com/file/d/1wKSrun-GlxirS3IZ9qoHazb9tC440AZF/view?usp=sharing]arrow_forward
- Refer to page 92 for a problem involving the stability of a fixed point in a nonlinear system of ODES. Linearize the system near the fixed point and determine its stability using eigenvalues of the Jacobian matrix. Instructions: Focus strictly on the stability analysis. Clearly outline the steps, including finding the Jacobian, determining eigenvalues, and concluding stability. Show all calculations. Link: [https://drive.google.com/file/d/1wKSrun-GlxirS3IZ9qoHazb9tC440AZF/view?usp=sharing]arrow_forwardRefer to page 75 for a problem involving the orthogonality of sine and cosine functions over a given interval. Provide a detailed proof by evaluating the appropriate integrals. Instructions: Provide step-by-step calculations showing the orthogonality proof clearly. Avoid unnecessary content and ensure every step is justified. Link: [https://drive.google.com/file/d/1wKSrun-GlxirS31Z9qoHazb9tC440AZF/view?usp=sharing]arrow_forwardLet f(z) be the function defined by the formula 1 f(z) = (2-1)(x-2)² (i) Find the Laurent series of f(z) about the point z = 1 that is valid in the region {z = C: |z − 1| > 1}. (ii) Find the Laurent series of f(2) about the point z = region { € C: 0 < | z − 2| < 1}. 2 that is valid in thearrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt
Elementary AlgebraAlgebraISBN:9780998625713Author:Lynn Marecek, MaryAnne Anthony-SmithPublisher:OpenStax - Rice University
Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill
Algebra: Structure And Method, Book 1
Algebra
ISBN:9780395977224
Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:McDougal Littell
Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL
Big Ideas Math A Bridge To Success Algebra 1: Stu...
Algebra
ISBN:9781680331141
Author:HOUGHTON MIFFLIN HARCOURT
Publisher:Houghton Mifflin Harcourt
Elementary Algebra
Algebra
ISBN:9780998625713
Author:Lynn Marecek, MaryAnne Anthony-Smith
Publisher:OpenStax - Rice University
How to make Frequency Distribution Table / Tally Marks and Frequency Distribution Table; Author: Reenu Math;https://www.youtube.com/watch?v=i_A6RiE8tLE;License: Standard YouTube License, CC-BY
Frequency distribution table in statistics; Author: Math and Science;https://www.youtube.com/watch?v=T7KYO76DoOE;License: Standard YouTube License, CC-BY
Frequency Distribution Table for Grouped/Continuous data | Math Dot Com; Author: Maths dotcom;https://www.youtube.com/watch?v=ErnccbXQOPY;License: Standard Youtube License