GEN CMB LL PRECALC ALEKS 360
GEN CMB LL PRECALC ALEKS 360
1st Edition
ISBN: 9781264657506
Author: Miller
Publisher: MCG CUSTOM
bartleby

Concept explainers

Equations and Inequations
Equations and inequalities describe the relationship between two mathematical expressions.
Linear Functions
A linear function can just be a constant, or it can be the constant multiplied with the variable like x or y. If the variables are of the form, x2, x1/2 or y2 it is not linear. The exponent over the variables should always be 1.
bartleby

Videos

Textbook Question
Book Icon
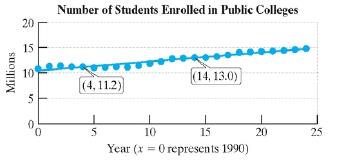
Chapter 1.5, Problem 64PE

The graph shows the number of students enrolled in public colleges for selected years. The x variable represents the number of years since 1990 and the y variable represents the number of students (in millions).

Chapter 1.5, Problem 64PE, The graph shows the number of students enrolled in public colleges for selected years. The x

a. Use the points (4, 11.2) and (14, 13.0) to write a linear model for these data.

b. Interpret the meaning of the slope in the context of this problem.

c. Interpret the meaning of the y -intercept in the context of this problem.

d. In the event that the linear trend continues beyond the last observed data point, use the model in part (a) to predict the number of students enrolled in public colleges for the year 2020.

Expert Solution & Answer
Check Mark

Want to see the full answer?

Check out a sample textbook solution
Blurred answer
Previous
Chapter 1.5, Problem 63PE
Next
Chapter 1.5, Problem 65PE
Students have asked these similar questions
4. Use method of separation of variable to solve the following wave equation მłu J²u subject to u(0,t) =0, for t> 0, u(л,t) = 0, for t> 0, = t> 0, at² ax²' u(x, 0) = 0, 0.01 x, ut(x, 0) = Π 0.01 (π-x), 0
Solve the following heat equation by method of separation variables: ди = at subject to u(0,t) =0, for -16024 ძx2 • t>0, 0 0, ux (4,t) = 0, for t> 0, u(x, 0) = (x-3, \-1, 0 < x ≤2 2≤ x ≤ 4.
ex 5. important aspects. Graph f(x)=lnx. Be sure to make your graph big enough to easily read (use the space given.) Label all 6 33

Chapter 1 Solutions

GEN CMB LL PRECALC ALEKS 360

Ch. 1.1 - Find the distance between the points 1,4and3,6 ....Ch. 1.1 - Determine if the points X6,4,Y2,2,andZ0,5 form the...Ch. 1.1 - Prob. 3SPCh. 1.1 - Prob. 4SPCh. 1.1 - Prob. 5SPCh. 1.1 - Given the equation y=x24,...Ch. 1.1 - Prob. 7SPCh. 1.1 - In a rectangular coordinate system, the point...Ch. 1.1 - Prob. 2PECh. 1.1 - Prob. 3PE
Ch. 1.1 - Prob. 4PECh. 1.1 - Prob. 5PECh. 1.1 - Prob. 6PECh. 1.1 - A y-intercept of a graph has an x-coordinate of .Ch. 1.1 - Prob. 8PECh. 1.1 - Prob. 9PECh. 1.1 - For Exercises 9-10, plot the points on a...Ch. 1.1 - For Exercises 11-18, a. Find the exact distance...Ch. 1.1 - Prob. 12PECh. 1.1 - For Exercises 11-18, a. Find the exact distance...Ch. 1.1 - For Exercises 11-18, a. Find the exact distance...Ch. 1.1 - Prob. 15PECh. 1.1 - For Exercises 11-18, a. Find the exact distance...Ch. 1.1 - Prob. 17PECh. 1.1 - Prob. 18PECh. 1.1 - Prob. 19PECh. 1.1 - For Exercises 19-22, determine if the given points...Ch. 1.1 - Prob. 21PECh. 1.1 - For Exercises 19-22, determine if the given points...Ch. 1.1 - For Exercises 23-24, determine if the given points...Ch. 1.1 - For Exercises 23-24, determine if the given points...Ch. 1.1 - Prob. 25PECh. 1.1 - For Exercises 25-30, identify the set of value x...Ch. 1.1 - For Exercises 25-30, identify the set of value x...Ch. 1.1 - Prob. 28PECh. 1.1 - For Exercises 25-30, identify the set of value x...Ch. 1.1 - Prob. 30PECh. 1.1 - For Exercises 31-44, graph the equation by...Ch. 1.1 - For Exercises 31-44, graph the equation by...Ch. 1.1 - Prob. 33PECh. 1.1 - For Exercises 31-44, graph the equation by...Ch. 1.1 - For Exercises 31-44, graph the equation by...Ch. 1.1 - For Exercises 31-44, graph the equation by...Ch. 1.1 - For Exercises 31-44, graph the equation by...Ch. 1.1 - Prob. 38PECh. 1.1 - Prob. 39PECh. 1.1 - For Exercises 31-44, graph the equation by...Ch. 1.1 - For Exercises 31-44, graph the equation by...Ch. 1.1 - For Exercises 31-44, graph the equation by...Ch. 1.1 - Prob. 43PECh. 1.1 - Prob. 44PECh. 1.1 - Prob. 45PECh. 1.1 - For Exercises 45-50, estimate the...Ch. 1.1 - For Exercises 45-50, estimate the...Ch. 1.1 - Prob. 48PECh. 1.1 - Prob. 49PECh. 1.1 - For Exercises 45-50, estimate the...Ch. 1.1 - For Exercises 51-62, find the x-andy-intercepts....Ch. 1.1 - For Exercises 51-62, find the x-andy-intercepts....Ch. 1.1 - For Exercises 51-62, find the x-andy-intercepts....Ch. 1.1 - For Exercises 51-62, find the x-andy-intercepts....Ch. 1.1 - Prob. 55PECh. 1.1 - For Exercises 51-62, find the x-andy-intercepts....Ch. 1.1 - For Exercises 51-62, find the x-andy-intercepts....Ch. 1.1 - For Exercises 51-62, find the x-andy-intercepts....Ch. 1.1 - For Exercises 51-62, find the x-andy-intercepts....Ch. 1.1 - For Exercises 51-62, find the x-andy-intercepts....Ch. 1.1 - For Exercises 51-62, find the x-andy-intercepts....Ch. 1.1 - Prob. 62PECh. 1.1 - A map of a wilderness area is drawn with the...Ch. 1.1 - A map of a state park is draw so that the origin...Ch. 1.1 - The position of an object in a video game is...Ch. 1.1 - Prob. 66PECh. 1.1 - Verify that the points A0,0,Bx,0,andC12x,32x make...Ch. 1.1 - Verify that the points A0,0,Bx,0,andC0,x make up...Ch. 1.1 - Prob. 69PECh. 1.1 - For Exercises 69-70, assume that the units shown...Ch. 1.1 - Prob. 71PECh. 1.1 - For Exercises 71-72, the endpoints of a diameter...Ch. 1.1 - For Exercises 73-74, an isosceles triangle is...Ch. 1.1 - Prob. 74PECh. 1.1 - For Exercises 75-78, determine if points A,B,andC...Ch. 1.1 - For Exercises 75-78, determine if points A,B,andC...Ch. 1.1 - Prob. 77PECh. 1.1 - For Exercises 75-78, determine if points A,B,andC...Ch. 1.1 - Suppose that d represents the distance between two...Ch. 1.1 - Prob. 80PECh. 1.1 - Explain how to find the x-andy-intercepts from an...Ch. 1.1 - Prob. 82PECh. 1.1 - Prob. 83PECh. 1.1 - A point in three-dimensional space can be...Ch. 1.1 - Prob. 85PECh. 1.1 - A point in three-dimensional space can be...Ch. 1.1 - What is meant by a viewing window on a graphing...Ch. 1.1 - Which of the viewing windows would show both the...Ch. 1.1 - For Exercises 89-92, graph the equation with a...Ch. 1.1 - For Exercises 89-92, graph the equation with a...Ch. 1.1 - For Exercises 89-92, graph the equation with a...Ch. 1.1 - For Exercises 89-92, graph the equation with a...Ch. 1.1 - For Exercises 93-94, graph the equations on the...Ch. 1.1 - For Exercises 93-94, graph the equations on the...Ch. 1.2 - Prob. 1SPCh. 1.2 - Prob. 2SPCh. 1.2 - Prob. 3SPCh. 1.2 - Write the equation in the form xh2+yk2=r2 , and...Ch. 1.2 - A is the set of all points in a equidistant from...Ch. 1.2 - Prob. 2PECh. 1.2 - Prob. 3PECh. 1.2 - Prob. 4PECh. 1.2 - Prob. 5PECh. 1.2 - Prob. 6PECh. 1.2 - Prob. 7PECh. 1.2 - Prob. 8PECh. 1.2 - Prob. 9PECh. 1.2 - Prob. 10PECh. 1.2 - Prob. 11PECh. 1.2 - Prob. 12PECh. 1.2 - Prob. 13PECh. 1.2 - Prob. 14PECh. 1.2 - Prob. 15PECh. 1.2 - Prob. 16PECh. 1.2 - Prob. 17PECh. 1.2 - Prob. 18PECh. 1.2 - Prob. 19PECh. 1.2 - Prob. 20PECh. 1.2 - Prob. 21PECh. 1.2 - Prob. 22PECh. 1.2 - Prob. 23PECh. 1.2 - Prob. 24PECh. 1.2 - Prob. 25PECh. 1.2 - Prob. 26PECh. 1.2 - Prob. 27PECh. 1.2 - Prob. 28PECh. 1.2 - Prob. 29PECh. 1.2 - Prob. 30PECh. 1.2 - Prob. 31PECh. 1.2 - Prob. 32PECh. 1.2 - Write an equation that represent the set of points...Ch. 1.2 - Write an equation that represent the set of points...Ch. 1.2 - Prob. 35PECh. 1.2 - Write an equation of the circle that is tangent to...Ch. 1.2 - Determine the solution set for the equation...Ch. 1.2 - Prob. 38PECh. 1.2 - Prob. 39PECh. 1.2 - Determine the solution set for the equation...Ch. 1.2 - For Exercise 41-54, write the equation in the form...Ch. 1.2 - For Exercise 41-54, write the equation in the form...Ch. 1.2 - For Exercise 41-54, write the equation in the form...Ch. 1.2 - For Exercise 41-54, write the equation in the form...Ch. 1.2 - For Exercise 41-54, write the equation in the form...Ch. 1.2 - For Exercise 41-54, write the equation in the form...Ch. 1.2 - For Exercise 41-54, write the equation in the form...Ch. 1.2 - Prob. 48PECh. 1.2 - Prob. 49PECh. 1.2 - For Exercise 41-54, write the equation in the form...Ch. 1.2 - For Exercise 41-54, write the equation in the form...Ch. 1.2 - For Exercise 41-54, write the equation in the form...Ch. 1.2 - Prob. 53PECh. 1.2 - For Exercise 41-54, write the equation in the form...Ch. 1.2 - A cell tower is a site where antennas,...Ch. 1.2 - A radar transmitter on a ship has a range of 20...Ch. 1.2 - Suppose that three geological study areas are set...Ch. 1.2 - Prob. 58PECh. 1.2 - State the definition of a circle.Ch. 1.2 - Prob. 60PECh. 1.2 - Find all values of y such that the distance is...Ch. 1.2 - Find all values of x such that the distance...Ch. 1.2 - Prob. 63PECh. 1.2 - Find all points on the line y=x that are 4 units...Ch. 1.2 - The general form of an equation of a circle is...Ch. 1.2 - The general form of an equation of a circle is...Ch. 1.2 - The general form of an equation of a circle is...Ch. 1.2 - The general form of an equation of a circle is...Ch. 1.2 - Find the shortest distance from the origin to a...Ch. 1.2 - Find the shortest distance from the origin to a...Ch. 1.2 - For Exercises 71-74, use a graphing calculator to...Ch. 1.2 - For Exercises 71-74, use a graphing calculator to...Ch. 1.2 - For Exercises 71-74, use a graphing calculator to...Ch. 1.2 - For Exercises 71-74, use a graphing calculator to...Ch. 1.3 - For the table shown, a. Write the set of ordered...Ch. 1.3 - Determine if the relation defines y as a function...Ch. 1.3 - Determine if the given relation defines y as a...Ch. 1.3 - Determine if the relation defines y as a function...Ch. 1.3 - Evaluate the function defined by hx=4x3 for the...Ch. 1.3 - Evaluate the function defined by fx=x2+4x for the...Ch. 1.3 - Find the x-andy-intercepts of the function defined...Ch. 1.3 - Determine the domain and range for the functions...Ch. 1.3 - Write the domain of each function in interval...Ch. 1.3 - Use the function f pictured to find:...Ch. 1.3 - A set of ordered pairs x,y is called a in xandy ....Ch. 1.3 - Given a function defined by y=fx, the statement...Ch. 1.3 - Given a function defined by y=fx, to find the ...Ch. 1.3 - Given a function defined by y=fx, to find the...Ch. 1.3 - Given fx=x+1x+5 , the domain is restricted so that...Ch. 1.3 - Given gx=x5, the domain is restricted so that x.Ch. 1.3 - Consider a relation that defines the height y of a...Ch. 1.3 - Consider a relation that define a time y during...Ch. 1.3 - For Exercises 9-12, a. Write a set of ordered...Ch. 1.3 - For Exercises 9-12, a. Write a set of ordered...Ch. 1.3 - For Exercises 9-12, a. Write a set of ordered...Ch. 1.3 - For Exercises 9-12, a. Write a set of ordered...Ch. 1.3 - Answer true or false. All relations are relations.Ch. 1.3 - Answer true or false. All relations are functions.Ch. 1.3 - For Exercises 15-32, determine if the relation...Ch. 1.3 - For Exercises 15-32, determine if the relation...Ch. 1.3 - For Exercises 15-32, determine if the relation...Ch. 1.3 - For Exercises 15-32, determine if the relation...Ch. 1.3 - Prob. 19PECh. 1.3 - For Exercises 15-32, determine if the relation...Ch. 1.3 - For Exercises 15-32, determine if the relation...Ch. 1.3 - For Exercises 15-32, determine if the relation...Ch. 1.3 - For Exercises 15-32, determine if the relation...Ch. 1.3 - Prob. 24PECh. 1.3 - For Exercises 15-32, determine if the relation...Ch. 1.3 - For Exercises 15-32, determine if the relation...Ch. 1.3 - Prob. 27PECh. 1.3 - For Exercises 15-32, determine if the relation...Ch. 1.3 - Prob. 29PECh. 1.3 - Prob. 30PECh. 1.3 - For Exercises 15-32, determine if the relation...Ch. 1.3 - For Exercises 15-32, determine if the relation...Ch. 1.3 - Prob. 33PECh. 1.3 - The statement g7=5 corresponds to what ordered...Ch. 1.3 - For Exercises 35-56, evaluate the function for the...Ch. 1.3 - Prob. 36PECh. 1.3 - Prob. 37PECh. 1.3 - For Exercises 35-56, evaluate the function for the...Ch. 1.3 - For Exercises 35-56, evaluate the function for the...Ch. 1.3 - Prob. 40PECh. 1.3 - Prob. 41PECh. 1.3 - For Exercises 35-56, evaluate the function for the...Ch. 1.3 - For Exercises 35-56, evaluate the function for the...Ch. 1.3 - Prob. 44PECh. 1.3 - Prob. 45PECh. 1.3 - For Exercises 35-56, evaluate the function for the...Ch. 1.3 - Prob. 47PECh. 1.3 - For Exercises 35-56, evaluate the function for the...Ch. 1.3 - For Exercises 35-56, evaluate the function for the...Ch. 1.3 - Prob. 50PECh. 1.3 - Prob. 51PECh. 1.3 - For Exercises 35-56, evaluate the function for the...Ch. 1.3 - Prob. 53PECh. 1.3 - Prob. 54PECh. 1.3 - For Exercises 35-56, evaluate the function for the...Ch. 1.3 - For Exercises 35-56, evaluate the function for the...Ch. 1.3 - Prob. 57PECh. 1.3 - For Exercises 57-62, find and simplify fx+h. (See...Ch. 1.3 - Prob. 59PECh. 1.3 - Prob. 60PECh. 1.3 - For Exercises 57-62, find and simplify fx+h. (See...Ch. 1.3 - Prob. 62PECh. 1.3 - Prob. 63PECh. 1.3 - Prob. 64PECh. 1.3 - For Exercises 63-70, refer to the function...Ch. 1.3 - For Exercises 63-70, refer to the function...Ch. 1.3 - For Exercises 63-70, refer to the function...Ch. 1.3 - Prob. 68PECh. 1.3 - Prob. 69PECh. 1.3 - For Exercises 63-70, refer to the function...Ch. 1.3 - Prob. 71PECh. 1.3 - Frank needs to drive 250 mi from Daytona Beach to...Ch. 1.3 - At a restaurant, if a party has eight or more...Ch. 1.3 - A bookstore marks up the price of a book by 40 of...Ch. 1.3 - Prob. 75PECh. 1.3 - For Exercises 75-84, determine the...Ch. 1.3 - Prob. 77PECh. 1.3 - For Exercises 75-84, determine the...Ch. 1.3 - For Exercises 75-84, determine the...Ch. 1.3 - Prob. 80PECh. 1.3 - For Exercises 75-84, determine the...Ch. 1.3 - For Exercises 75-84, determine the...Ch. 1.3 - Prob. 83PECh. 1.3 - For Exercises 75-84, determine the...Ch. 1.3 - Prob. 85PECh. 1.3 - The amount spent on video games per person in the...Ch. 1.3 - For Exercises 87-96, determine the domain and...Ch. 1.3 - For Exercises 87-96, determine the domain and...Ch. 1.3 - For Exercises 87-96, determine the domain and...Ch. 1.3 - For Exercises 87-96, determine the domain and...Ch. 1.3 - Prob. 91PECh. 1.3 - For Exercises 87-96, determine the domain and...Ch. 1.3 - For Exercises 87-96, determine the domain and...Ch. 1.3 - For Exercises 87-96, determine the domain and...Ch. 1.3 - Prob. 95PECh. 1.3 - For Exercises 87-96, determine the domain and...Ch. 1.3 - For Exercises 97-110, write the domain in interval...Ch. 1.3 - For Exercises 97-110, write the domain in interval...Ch. 1.3 - For Exercises 97-110, write the domain in interval...Ch. 1.3 - For Exercises 97-110, write the domain in interval...Ch. 1.3 - For Exercises 97-110, write the domain in interval...Ch. 1.3 - Prob. 102PECh. 1.3 - For Exercises 97-110, write the domain in interval...Ch. 1.3 - For Exercises 97-110, write the domain in interval...Ch. 1.3 - For Exercises 97-110, write the domain in interval...Ch. 1.3 - For Exercises 97-110, write the domain in interval...Ch. 1.3 - For Exercises 97-110, write the domain in interval...Ch. 1.3 - Prob. 108PECh. 1.3 - For Exercises 97-110, write the domain in interval...Ch. 1.3 - Prob. 110PECh. 1.3 - For Exercises 111-114, use the graph of y=fx to...Ch. 1.3 - For Exercises 111-114, use the graph of y=fx to...Ch. 1.3 - Prob. 113PECh. 1.3 - Prob. 114PECh. 1.3 - For Exercises 115-122, write a function that...Ch. 1.3 - For Exercises 115-122, write a function that...Ch. 1.3 - Prob. 117PECh. 1.3 - Prob. 118PECh. 1.3 - For Exercises 115-122, write a function that...Ch. 1.3 - For Exercises 115-122, write a function that...Ch. 1.3 - Prob. 121PECh. 1.3 - For Exercises 115-122, write a function that...Ch. 1.3 - If two points align vertically then the points do...Ch. 1.3 - Prob. 124PECh. 1.3 - Given a square with sides of length s, diagonal of...Ch. 1.3 - Given a circle with radius r, diameter d,...Ch. 1.4 - Graph the line represented by each equation....Ch. 1.4 - Prob. 2SPCh. 1.4 - Prob. 3SPCh. 1.4 - Given 2x+4y=8, a. Write the equation in...Ch. 1.4 - Prob. 5SPCh. 1.4 - Refer to the graph in Example 6. a. Determine the...Ch. 1.4 - Prob. 7SPCh. 1.4 - Prob. 8SPCh. 1.4 - a. Solve the equation 3xx+41=0 and verify the...Ch. 1.4 - A equation in the variables xandy can be written...Ch. 1.4 - An equation of the form x=k where k is a constant...Ch. 1.4 - An equation of the form y=k where k is a constant...Ch. 1.4 - Write the formula for the slope of a line between...Ch. 1.4 - The slope of a horizontal line is and the slope...Ch. 1.4 - A function f is a liner function if fx=, where m...Ch. 1.4 - If f is defined on the interval x1,x2, then the...Ch. 1.4 - The graph of a constant function defined by fx=b...Ch. 1.4 - For Exercises 9-20, graph the equation and...Ch. 1.4 - For Exercises 9-20, graph the equation and...Ch. 1.4 - For Exercises 9-20, graph the equation and...Ch. 1.4 - For Exercises 9-20, graph the equation and...Ch. 1.4 - For Exercises 9-20, graph the equation and...Ch. 1.4 - For Exercises 9-20, graph the equation and...Ch. 1.4 - For Exercises 9-20, graph the equation and...Ch. 1.4 - For Exercises 9-20, graph the equation and...Ch. 1.4 - For Exercises 9-20, graph the equation and...Ch. 1.4 - For Exercises 9-20, graph the equation and...Ch. 1.4 - For Exercises 9-20, graph the equation and...Ch. 1.4 - For Exercises 9-20, graph the equation and...Ch. 1.4 - Find the average slope of the hill.Ch. 1.4 - Find the absolute value of the slope of the storm...Ch. 1.4 - The road sign shown in the figure indicate the...Ch. 1.4 - The pitch of a roof is defined as...Ch. 1.4 - For Exercises 25-36, determine the slope of the...Ch. 1.4 - For Exercises 25-36, determine the slope of the...Ch. 1.4 - For Exercises 25-36, determine the slope of the...Ch. 1.4 - For Exercises 25-36, determine the slope of the...Ch. 1.4 - For Exercises 25-36, determine the slope of the...Ch. 1.4 - For Exercises 25-36, determine the slope of the...Ch. 1.4 - For Exercises 25-36, determine the slope of the...Ch. 1.4 - For Exercises 25-36, determine the slope of the...Ch. 1.4 - For Exercises 25-36, determine the slope of the...Ch. 1.4 - For Exercises 25-36, determine the slope of the...Ch. 1.4 - For Exercises 25-36, determine the slope of the...Ch. 1.4 - For Exercises 25-36, determine the slope of the...Ch. 1.4 - For Exercises 37-42, determine the slope of the...Ch. 1.4 - For Exercises 37-42, determine the slope of the...Ch. 1.4 - For Exercises 37-42, determine the slope of the...Ch. 1.4 - For Exercises 37-42, determine the slope of the...Ch. 1.4 - For Exercises 37-42, determine the slope of the...Ch. 1.4 - For Exercises 37-42, determine the slope of the...Ch. 1.4 - What is the slope of a line perpendicular to the...Ch. 1.4 - What is the slope of a line defined by y=7?Ch. 1.4 - If the slope of a line is 45, how much vertical...Ch. 1.4 - Suppose that y=Pt represents the population of a...Ch. 1.4 - What is the slope of a line parallel to the...Ch. 1.4 - What is the slope of a line defined to the x=2?Ch. 1.4 - If the slope of a line is 58, how much horizontal...Ch. 1.4 - Suppose that y=dt represent the distance that an...Ch. 1.4 - For Exercises 51-62, a. Write the equation in...Ch. 1.4 - For Exercises 51-62, a. Write the equation in...Ch. 1.4 - For Exercises 51-62, a. Write the equation in...Ch. 1.4 - For Exercises 51-62, a. Write the equation in...Ch. 1.4 - For Exercises 51-62, a. Write the equation in...Ch. 1.4 - For Exercises 51-62, a. Write the equation in...Ch. 1.4 - For Exercises 51-62, a. Write the equation in...Ch. 1.4 - For Exercises 51-62, a. Write the equation in...Ch. 1.4 - For Exercises 51-62, a. Write the equation in...Ch. 1.4 - For Exercises 51-62, a. Write the equation in...Ch. 1.4 - For Exercises 51-62, a. Write the equation in...Ch. 1.4 - For Exercises 51-62, a. Write the equation in...Ch. 1.4 - For Exercises 63-64, determine if the function is...Ch. 1.4 - For Exercises 63-64, determine if the function is...Ch. 1.4 - For Exercises 65-74, a. Use slope-intercepts form...Ch. 1.4 - For Exercises 65-74, a. Use slope-intercepts form...Ch. 1.4 - For Exercises 65-74, a. Use slope-intercepts form...Ch. 1.4 - For Exercises 65-74, a. Use slope-intercepts form...Ch. 1.4 - For Exercises 65-74, a. Use slope-intercepts form...Ch. 1.4 - For Exercises 65-74, a. Use slope-intercepts form...Ch. 1.4 - For Exercises 65-74, a. Use slope-intercepts form...Ch. 1.4 - For Exercises 65-74, a. Use slope-intercepts form...Ch. 1.4 - For Exercises 65-74, a. Use slope-intercepts form...Ch. 1.4 - For Exercises 65-74, a. Use slope-intercepts form...Ch. 1.4 - For Exercises 75-78, a. Use slope-intercept form...Ch. 1.4 - For Exercises 75-78, a. Use slope-intercept form...Ch. 1.4 - For Exercises 75-78, a. Use slope-intercept form...Ch. 1.4 - For Exercises 75-78, a. Use slope-intercept form...Ch. 1.4 - For Exercises 79-80, find slope of the secant line...Ch. 1.4 - For Exercises 79-80, find slope of the secant line...Ch. 1.4 - The function given by y=fx shows the value of...Ch. 1.4 - The function given by y=fx shows the average...Ch. 1.4 - The number Nt of new cases of a flu outbreak for a...Ch. 1.4 - The speed vL (in m/sec) of an ocean wave in deep...Ch. 1.4 - For Exercises 85-90, determine the average rate of...Ch. 1.4 - For Exercises 85-90, determine the average rate of...Ch. 1.4 - For Exercises 85-90, determine the average rate of...Ch. 1.4 - For Exercises 85-90, determine the average rate of...Ch. 1.4 - For Exercises 85-90, determine the average rate of...Ch. 1.4 - For Exercises 85-90, determine the average rate of...Ch. 1.4 - For Exercises 91-98, use the graph to solve the...Ch. 1.4 - For Exercises 91-98, use the graph to solve the...Ch. 1.4 - For Exercises 91-98, use the graph to solve the...Ch. 1.4 - For Exercises 91-98, use the graph to solve the...Ch. 1.4 - For Exercises 91-98, use the graph to solve the...Ch. 1.4 - For Exercises 91-98, use the graph to solve the...Ch. 1.4 - For Exercises 91-98, use the graph to solve the...Ch. 1.4 - For Exercises 91-98, use the graph to solve the...Ch. 1.4 - Explain how you can determine from a linear...Ch. 1.4 - Explain how you can determine from a linear...Ch. 1.4 - What is the benefit of writing an equation of a...Ch. 1.4 - Explain how the average rate of change of a...Ch. 1.4 - Determine the area in the second quadrant enclosed...Ch. 1.4 - Determine the area enclosed by the equations....Ch. 1.4 - Determine the area enclosed by the equations....Ch. 1.4 - Determine the area enclosed by the equations....Ch. 1.4 - Consider the standard form of a linear equation...Ch. 1.4 - Use the results from Exercise 107 to determine the...Ch. 1.4 - For Exercises 109-112, solve the equation in part...Ch. 1.4 - For Exercises 109-112, solve the equation in part...Ch. 1.4 - For Exercises 109-112, solve the equation in part...Ch. 1.4 - For Exercises 109-112, solve the equation in part...Ch. 1.4 - For Exercises 113-114, graph the lines in (a)-(c)...Ch. 1.4 - For Exercises 113-114, graph the lines in (a)-(c)...Ch. 1.5 - Use the point-slope formula to find an equation of...Ch. 1.5 - Write an equation of the line passing through the...Ch. 1.5 - Prob. 3SPCh. 1.5 - Write an equation of the line passing through the...Ch. 1.5 - Prob. 5SPCh. 1.5 - Repeat Example 6 in the case where the vendor can...Ch. 1.5 - Suppose that y represents the average consumer...Ch. 1.5 - The data given represent the class averages for...Ch. 1.5 - Given a point x1,y1 on a line with slope m , the...Ch. 1.5 - If two nonvertical lines have the same slope but...Ch. 1.5 - If m1andm2 represent the slope of two nonvertical...Ch. 1.5 - Suppose that y=Cx represents the cost to produce x...Ch. 1.5 - For Exercises 5-20, use the point-slope formula to...Ch. 1.5 - For Exercises 5-20, use the point-slope formula to...Ch. 1.5 - Prob. 7PECh. 1.5 - Prob. 8PECh. 1.5 - For Exercises 5-20, use the point-slope formula to...Ch. 1.5 - For Exercises 5-20, use the point-slope formula to...Ch. 1.5 - Prob. 11PECh. 1.5 - Prob. 12PECh. 1.5 - Prob. 13PECh. 1.5 - For Exercises 5-20, use the point-slope formula to...Ch. 1.5 - For Exercises 5-20, use the point-slope formula to...Ch. 1.5 - For Exercises 5-20, use the point-slope formula to...Ch. 1.5 - Prob. 17PECh. 1.5 - For Exercises 5-20, use the point-slope formula to...Ch. 1.5 - Prob. 19PECh. 1.5 - For Exercises 5-20, use the point-slope formula to...Ch. 1.5 - Prob. 21PECh. 1.5 - Prob. 22PECh. 1.5 - For Exercises 23-28, the slope of a line is given....Ch. 1.5 - Prob. 24PECh. 1.5 - Prob. 25PECh. 1.5 - For Exercises 23-28, the slope of a line is given....Ch. 1.5 - Prob. 27PECh. 1.5 - Prob. 28PECh. 1.5 - For Exercises 29-36, determine if the lines...Ch. 1.5 - Prob. 30PECh. 1.5 - For Exercises 29-36, determine if the lines...Ch. 1.5 - Prob. 32PECh. 1.5 - Prob. 33PECh. 1.5 - For Exercises 29-36, determine if the lines...Ch. 1.5 - Prob. 35PECh. 1.5 - Prob. 36PECh. 1.5 - For exercises 37-44, write an equation of the line...Ch. 1.5 - For exercises 37-44, write an equation of the line...Ch. 1.5 - For exercises 37-44, write an equation of the line...Ch. 1.5 - For exercises 37-44, write an equation of the line...Ch. 1.5 - For exercises 37-44, write an equation of the line...Ch. 1.5 - For exercises 37-44, write an equation of the line...Ch. 1.5 - Prob. 43PECh. 1.5 - For exercises 37-44, write an equation of the line...Ch. 1.5 - For Exercises 45-50, write an equation of the line...Ch. 1.5 - Prob. 46PECh. 1.5 - Prob. 47PECh. 1.5 - Prob. 48PECh. 1.5 - For Exercises 45-50, write an equation of the line...Ch. 1.5 - For Exercises 45-50, write an equation of the line...Ch. 1.5 - A sales person makes a base salary of $400 per...Ch. 1.5 - At a parking garage in a large city, the charge...Ch. 1.5 - Millage rate is the amount per $1000 that is often...Ch. 1.5 - The average water level in a retention pond is 6.8...Ch. 1.5 - For Exercises 55-56, the fixed and variable costs...Ch. 1.5 - For Exercises 55-56, the fixed and variable costs...Ch. 1.5 - Prob. 57PECh. 1.5 - Prob. 58PECh. 1.5 - A small business makes cookies and sells them at...Ch. 1.5 - A lawn service company charges $60 for each lawn...Ch. 1.5 - The data in the graph show the wind speed y (in...Ch. 1.5 - Caroline adopted a puppy named Dodger from an...Ch. 1.5 - A paediatrician records the age xinyr and average...Ch. 1.5 - The graph shows the number of students enrolled in...Ch. 1.5 - The table gives the number of calories and the...Ch. 1.5 - The table gives the average gestation period for...Ch. 1.5 - Prob. 67PECh. 1.5 - Prob. 68PECh. 1.5 - Prob. 69PECh. 1.5 - Prob. 70PECh. 1.5 - The graph in Exercise 61 shows the wind speed y...Ch. 1.5 - Prob. 72PECh. 1.5 - The graph in Exercise 63 shows the average height...Ch. 1.5 - The graph in Exercise 64 shows the number of...Ch. 1.5 - Prob. 75PECh. 1.5 - Prob. 76PECh. 1.5 - Prob. 77PECh. 1.5 - Prob. 78PECh. 1.5 - Prob. 79PECh. 1.5 - Prob. 80PECh. 1.5 - Prob. 81PECh. 1.5 - Prob. 82PECh. 1.5 - Prob. 83PECh. 1.5 - Prob. 84PECh. 1.5 - Prob. 85PECh. 1.5 - Prob. 86PECh. 1.5 - Prob. 87PECh. 1.5 - Prob. 88PECh. 1.5 - Prob. 89PECh. 1.5 - Prob. 90PECh. 1.5 - Prob. 91PECh. 1.5 - Prob. 92PECh. 1.5 - Prob. 1PRECh. 1.5 - Prob. 2PRECh. 1.5 - Prob. 3PRECh. 1.5 - Prob. 4PRECh. 1.5 - Prob. 5PRECh. 1.5 - Prob. 6PRECh. 1.5 - Prob. 7PRECh. 1.5 - Prob. 8PRECh. 1.5 - Prob. 9PRECh. 1.5 - Prob. 10PRECh. 1.5 - Prob. 11PRECh. 1.5 - Prob. 12PRECh. 1.5 - Prob. 13PRECh. 1.5 - Prob. 14PRECh. 1.5 - Prob. 15PRECh. 1.5 - Prob. 16PRECh. 1.5 - Prob. 17PRECh. 1.5 - For Exercises 9-18, graph the functions by...Ch. 1.6 - Use translations to graph the given functions....Ch. 1.6 - Graph the function defined by gx=x+2.Ch. 1.6 - Use translations to graph the function defined by...Ch. 1.6 - Graph the functions. a.fx=x2b.gx=3x2c.hx=13x2Ch. 1.6 - The graph of y=fx is shown. Graph. a.y=f2xb.y=f12xCh. 1.6 - Prob. 6SPCh. 1.6 - Prob. 7SPCh. 1.6 - Use transformations to graph the function defined...Ch. 1.6 - Let c represent a positive real number. The graph...Ch. 1.6 - Prob. 2PECh. 1.6 - Let c represent a positive real number. The graph...Ch. 1.6 - The graph of y=3fx is the graph of y=fx with a...Ch. 1.6 - Prob. 5PECh. 1.6 - The graph of y=f13x is the graph of y=fx with a...Ch. 1.6 - The graph of y=13fx is the graph of y=fx with a...Ch. 1.6 - The graph of y=fx is the graph of y=fx reflected...Ch. 1.6 - For Exercises 9-14, from memory match the equation...Ch. 1.6 - For Exercises 9-14, from memory match the equation...Ch. 1.6 - Prob. 11PECh. 1.6 - For Exercises 9-14, from memory match the equation...Ch. 1.6 - Prob. 13PECh. 1.6 - For Exercises 9-14, from memory match the equation...Ch. 1.6 - For Exercises 15-26, use translations to graph the...Ch. 1.6 - For Exercises 15-26, use translations to graph the...Ch. 1.6 - For Exercises 15-26, use translations to graph the...Ch. 1.6 - For Exercises 15-26, use translations to graph the...Ch. 1.6 - Prob. 19PECh. 1.6 - For Exercises 15-26, use translations to graph the...Ch. 1.6 - Prob. 21PECh. 1.6 - For Exercises 15-26, use translations to graph the...Ch. 1.6 - For Exercises 15-26, use translations to graph the...Ch. 1.6 - For Exercises 15-26, use translations to graph the...Ch. 1.6 - For Exercises 15-26, use translations to graph the...Ch. 1.6 - Prob. 26PECh. 1.6 - For Exercises 27-32, use transformations to graph...Ch. 1.6 - For Exercises 27-32, use transformations to graph...Ch. 1.6 - For Exercises 27-32, use transformations to graph...Ch. 1.6 - For Exercises 27-32, use transformations to graph...Ch. 1.6 - For Exercises 27-32, use transformations to graph...Ch. 1.6 - For Exercises 27-32, use transformations to graph...Ch. 1.6 - For Exercises 33-40, use the graphs of y=fxandy=gx...Ch. 1.6 - For Exercises 33-40, use the graphs of y=fxandy=gx...Ch. 1.6 - For Exercises 33-40, use the graphs of y=fxandy=gx...Ch. 1.6 - For Exercises 33-40, use the graphs of y=fxandy=gx...Ch. 1.6 - For Exercises 33-40, use the graphs of y=fxandy=gx...Ch. 1.6 - For Exercises 33-40, use the graphs of y=fxandy=gx...Ch. 1.6 - For Exercises 33-40, use the graphs of y=fxandy=gx...Ch. 1.6 - For Exercises 33-40, use the graphs of y=fxandy=gx...Ch. 1.6 - For Exercises 41-46, graph the function by...Ch. 1.6 - For Exercises 41-46, graph the function by...Ch. 1.6 - For Exercises 41-46, graph the function by...Ch. 1.6 - For Exercises 41-46, graph the function by...Ch. 1.6 - For Exercises 41-46, graph the function by...Ch. 1.6 - For Exercises 41-46, graph the function by...Ch. 1.6 - For Exercises 47-50, use the graph of y=fxandy=gx...Ch. 1.6 - For Exercises 47-50, use the graph of y=fxandy=gx...Ch. 1.6 - For Exercises 47-50, use the graph of y=fxandy=gx...Ch. 1.6 - For Exercises 47-50, use the graph of y=fxandy=gx...Ch. 1.6 - For Exercises 51-54, use the graphs of y=fxandy=gx...Ch. 1.6 - For Exercises 51-54, use the graphs of y=fxandy=gx...Ch. 1.6 - For Exercises 51-54, use the graphs of y=fxandy=gx...Ch. 1.6 - For Exercises 51-54, use the graphs of y=fxandy=gx...Ch. 1.6 - For Exercises 55-62, a function g is given....Ch. 1.6 - Prob. 56PECh. 1.6 - For Exercises 55-62, a function g is given....Ch. 1.6 - Prob. 58PECh. 1.6 - Prob. 59PECh. 1.6 - For Exercises 55-62, a function g is given....Ch. 1.6 - Prob. 61PECh. 1.6 - Prob. 62PECh. 1.6 - For Exercises 63-78, use transformations to graph...Ch. 1.6 - For Exercises 63-78, use transformations to graph...Ch. 1.6 - Prob. 65PECh. 1.6 - Prob. 66PECh. 1.6 - For Exercises 63-78, use transformations to graph...Ch. 1.6 - Prob. 68PECh. 1.6 - Prob. 69PECh. 1.6 - For Exercises 63-78, use transformations to graph...Ch. 1.6 - Prob. 71PECh. 1.6 - For Exercises 63-78, use transformations to graph...Ch. 1.6 - For Exercises 63-78, use transformations to graph...Ch. 1.6 - Prob. 74PECh. 1.6 - For Exercises 63-78, use transformations to graph...Ch. 1.6 - For Exercises 63-78, use transformations to graph...Ch. 1.6 - Prob. 77PECh. 1.6 - Prob. 78PECh. 1.6 - For Exercises 79-86, the graph of y=fx is given....Ch. 1.6 - For Exercises 79-86, the graph of y=fx is given....Ch. 1.6 - For Exercises 79-86, the graph of y=fx is given....Ch. 1.6 - For Exercises 79-86, the graph of y=fx is given....Ch. 1.6 - For Exercises 79-86, the graph of y=fx is given....Ch. 1.6 - Prob. 84PECh. 1.6 - For Exercises 79-86, the graph of y=fx is given....Ch. 1.6 - Prob. 86PECh. 1.6 - For Exercises 87-90, write a function based on the...Ch. 1.6 - For Exercises 87-90, write a function based on the...Ch. 1.6 - For Exercises 87-90, write a function based on the...Ch. 1.6 - For Exercises 87-90, write a function based on the...Ch. 1.6 - Explain why the graph of gx=2x can be interpreted...Ch. 1.6 - Explain why the graph of hx=12x can be interpreted...Ch. 1.6 - Prob. 93PECh. 1.6 - Explain why gx=1x+1 can be graphed by shifting the...Ch. 1.6 - For Exercises 95-100, use transformations on the...Ch. 1.6 - For Exercises 95-100, use transformations on the...Ch. 1.6 - Prob. 97PECh. 1.6 - For Exercises 95-100, use transformations on the...Ch. 1.6 - For Exercises 95-100, use transformations on the...Ch. 1.6 - Prob. 100PECh. 1.6 - The graph shows the number of views y (in...Ch. 1.6 - Prob. 102PECh. 1.6 - a. Graph the functions on the viewing window...Ch. 1.7 - Determine whether the graph is symmetric with...Ch. 1.7 - Prob. 2SPCh. 1.7 - Determine if the function is even, odd, or...Ch. 1.7 - Determine if the function is even, odd, or...Ch. 1.7 - Evaluate the function for the given value of x....Ch. 1.7 - Graph the function. fx=2forx12xforx1Ch. 1.7 - Graph the function. fx=xfor4x2x+2forx2Ch. 1.7 - Evaluate fx=x for the given values of x....Ch. 1.7 - Prob. 9SPCh. 1.7 - Use interval notation to write the interval(s)...Ch. 1.7 - For the graph shown, a. Determine the location and...Ch. 1.7 - A graph of an equation is symmetric with respect...Ch. 1.7 - A graph of an equation is symmetric with respect...Ch. 1.7 - A graph of an equation is symmetric with respect...Ch. 1.7 - An even function is symmetric with respect to the ...Ch. 1.7 - An odd function is symmetric with respect to the ...Ch. 1.7 - The expression represents the greatest integer,...Ch. 1.7 - For Exercises 7-18, determine whether the graph of...Ch. 1.7 - For Exercises 7-18, determine whether the graph of...Ch. 1.7 - For Exercises 7-18, determine whether the graph of...Ch. 1.7 - For Exercises 7-18, determine whether the graph of...Ch. 1.7 - For Exercises 7-18, determine whether the graph of...Ch. 1.7 - For Exercises 7-18, determine whether the graph of...Ch. 1.7 - For Exercises 7-18, determine whether the graph of...Ch. 1.7 - For Exercises 7-18, determine whether the graph of...Ch. 1.7 - For Exercises 7-18, determine whether the graph of...Ch. 1.7 - For Exercises 7-18, determine whether the graph of...Ch. 1.7 - For Exercises 7-18, determine whether the graph of...Ch. 1.7 - For Exercises 7-18, determine whether the graph of...Ch. 1.7 - Prob. 19PECh. 1.7 - Prob. 20PECh. 1.7 - For exercises 21-26, use the graph to determine if...Ch. 1.7 - For exercises 21-26, use the graph to determine if...Ch. 1.7 - For exercises 21-26, use the graph to determine if...Ch. 1.7 - For exercises 21-26, use the graph to determine if...Ch. 1.7 - Prob. 25PECh. 1.7 - For exercises 21-26, use the graph to determine if...Ch. 1.7 - ...Ch. 1.7 - ...Ch. 1.7 - ...Ch. 1.7 - ...Ch. 1.7 - ...Ch. 1.7 - ...Ch. 1.7 - For Exercises 33-46, determine if the function is...Ch. 1.7 - For Exercises 33-46, determine if the function is...Ch. 1.7 - For Exercises 33-46, determine if the function is...Ch. 1.7 - For Exercises 33-46, determine if the function is...Ch. 1.7 - For Exercises 33-46, determine if the function is...Ch. 1.7 - For Exercises 33-46, determine if the function is...Ch. 1.7 - For Exercises 33-46, determine if the function is...Ch. 1.7 - For Exercises 33-46, determine if the function is...Ch. 1.7 - For Exercises 33-46, determine if the function is...Ch. 1.7 - For Exercises 33-46, determine if the function is...Ch. 1.7 - For Exercises 33-46, determine if the function is...Ch. 1.7 - For Exercises 33-46, determine if the function is...Ch. 1.7 - For Exercises 33-46, determine if the function is...Ch. 1.7 - For Exercises 33-46, determine if the function is...Ch. 1.7 - For Exercises 47-50, evaluate the function for the...Ch. 1.7 - For Exercises 47-50, evaluate the function for the...Ch. 1.7 - For Exercises 47-50, evaluate the function for the...Ch. 1.7 - For Exercises 47-50, evaluate the function for the...Ch. 1.7 - A sled accelerates down a hill and then slows down...Ch. 1.7 - A car starts from rest and accelerates to a speed...Ch. 1.7 - For Exercises 53-56, match the function with its...Ch. 1.7 - For Exercises 53-56, match the function with its...Ch. 1.7 - For Exercises 53-56, match the function with its...Ch. 1.7 - For Exercises 53-56, match the function with its...Ch. 1.7 - ...Ch. 1.7 - ...Ch. 1.7 - Prob. 59PECh. 1.7 - ...Ch. 1.7 - For Exercises 61-70, graph the function. (See...Ch. 1.7 - For Exercises 61-70, graph the function. (See...Ch. 1.7 - For Exercises 61-70, graph the function. (See...Ch. 1.7 - Prob. 64PECh. 1.7 - For Exercises 61-70, graph the function. (See...Ch. 1.7 - Prob. 66PECh. 1.7 - Prob. 67PECh. 1.7 - Prob. 68PECh. 1.7 - For Exercises 61-70, graph the function. (See...Ch. 1.7 - For Exercises 61-70, graph the function. (See...Ch. 1.7 - Prob. 71PECh. 1.7 - For Exercise 72-80, evaluate the step function...Ch. 1.7 - For Exercise 72-80, evaluate the step function...Ch. 1.7 - For Exercise 72-80, evaluate the step function...Ch. 1.7 - Prob. 75PECh. 1.7 - Prob. 76PECh. 1.7 - For Exercise 72-80, evaluate the step function...Ch. 1.7 - Prob. 78PECh. 1.7 - Prob. 79PECh. 1.7 - For Exercise 72-80, evaluate the step function...Ch. 1.7 - Prob. 81PECh. 1.7 - For Exercises 81-84, graph the function. (See...Ch. 1.7 - Prob. 83PECh. 1.7 - For Exercises 81-84, graph the function. (See...Ch. 1.7 - For a recent year, the rate for first class...Ch. 1.7 - The water level in a retention pond started at 5...Ch. 1.7 - A salesperson makes a base salary of $2000 per...Ch. 1.7 - A cell phone plan charges $49.95 per month plus...Ch. 1.7 - For Exercise 89-96, use interval notation to write...Ch. 1.7 - For Exercise 89-96, use interval notation to write...Ch. 1.7 - For Exercise 89-96, use interval notation to write...Ch. 1.7 - For Exercise 89-96, use interval notation to write...Ch. 1.7 - For Exercise 89-96, use interval notation to write...Ch. 1.7 - For Exercise 89-96, use interval notation to write...Ch. 1.7 - For Exercise 89-96, use interval notation to write...Ch. 1.7 - For Exercise 89-96, use interval notation to write...Ch. 1.7 - For Exercises 97-102, identify the location and...Ch. 1.7 - For Exercises 97-102, identify the location and...Ch. 1.7 - Prob. 99PECh. 1.7 - For Exercises 97-102, identify the location and...Ch. 1.7 - Prob. 101PECh. 1.7 - For Exercises 97-102, identify the location and...Ch. 1.7 - The graph shows the depth d (in ft) of a retention...Ch. 1.7 - The graph shows the height h (in meters) of a...Ch. 1.7 - For Exercises 105-110, produce a rule for the...Ch. 1.7 - Prob. 106PECh. 1.7 - For Exercises 105-110, produce a rule for the...Ch. 1.7 - Prob. 108PECh. 1.7 - Prob. 109PECh. 1.7 - Prob. 110PECh. 1.7 - For Exercises 111-112, a. Graph the function. b....Ch. 1.7 - Prob. 112PECh. 1.7 - Prob. 113PECh. 1.7 - Prob. 114PECh. 1.7 - From an equation in xandy, explain how to...Ch. 1.7 - Prob. 116PECh. 1.7 - Prob. 117PECh. 1.7 - Prob. 118PECh. 1.7 - Provide an informal explanation of a relative...Ch. 1.7 - Prob. 120PECh. 1.7 - Prob. 121PECh. 1.7 - Prob. 122PECh. 1.7 - A graph is concave up on a given interval if it...Ch. 1.7 - Prob. 124PECh. 1.7 - Prob. 125PECh. 1.7 - A graph is concave up on a given interval if it...Ch. 1.7 - For a recent year, the federal income tax owed by...Ch. 1.7 - For Exercises 128-131, use a graphing utility to...Ch. 1.7 - For Exercises 128-131, use a graphing utility to...Ch. 1.7 - For Exercises 128-131, use a graphing utility to...Ch. 1.7 - For Exercises 128-131, use a graphing utility to...Ch. 1.7 - For Exercises 132-135, use a graphing utility to...Ch. 1.7 - For Exercises 132-135, use a graphing utility to...Ch. 1.7 - For Exercises 132-135, use a graphing utility to...Ch. 1.7 - For Exercises 132-135, use a graphing utility to...Ch. 1.8 - Given mx=xandnx=4,findm+nx.Ch. 1.8 - Prob. 2SPCh. 1.8 - Prob. 3SPCh. 1.8 - ...Ch. 1.8 - ...Ch. 1.8 - Prob. 6SPCh. 1.8 - Given fx=3x+4andgx=1x1, write a rule for each...Ch. 1.8 - Prob. 8SPCh. 1.8 - Given rx=xx+1andtx=5x29,findrtx and write the...Ch. 1.8 - An artist shops online for tubes of watercolor...Ch. 1.8 - Prob. 11SPCh. 1.8 - Refer to the functions fandg pictured in Example...Ch. 1.8 - Prob. 1PECh. 1.8 - The function fg is defined by fgx= provided that ...Ch. 1.8 - Let h represent a positive real number. Given a...Ch. 1.8 - The composition of fandg, denoted by fg, is...Ch. 1.8 - For Exercises 5-8, find f+gx and identify the...Ch. 1.8 - For Exercises 5-8, find f+gx and identify the...Ch. 1.8 - For Exercises 5-8, find f+gx and identify the...Ch. 1.8 - For Exercises 5-8, find f+gx and identify the...Ch. 1.8 - For Exercises 9-18, evaluate the functions for the...Ch. 1.8 - For Exercises 9-18, evaluate the functions for the...Ch. 1.8 - For Exercises 9-18, evaluate the functions for the...Ch. 1.8 - For Exercises 9-18, evaluate the functions for the...Ch. 1.8 - For Exercises 9-18, evaluate the functions for the...Ch. 1.8 - For Exercises 9-18, evaluate the functions for the...Ch. 1.8 - For Exercises 9-18, evaluate the functions for the...Ch. 1.8 - For Exercises 9-18, evaluate the functions for the...Ch. 1.8 - For Exercises 9-18, evaluate the functions for the...Ch. 1.8 - For Exercises 9-18, evaluate the functions for the...Ch. 1.8 - For Exercises 19-26, refer to the functions...Ch. 1.8 - For Exercises 19-26, refer to the functions...Ch. 1.8 - For Exercises 19-26, refer to the functions...Ch. 1.8 - For Exercises 19-26, refer to the functions...Ch. 1.8 - For Exercises 19-26, refer to the functions...Ch. 1.8 - For Exercises 19-26, refer to the functions...Ch. 1.8 - For Exercises 19-26, refer to the functions...Ch. 1.8 - For Exercises 19-26, refer to the functions...Ch. 1.8 - For Exercises 27-32, refer to functions s,t,andv....Ch. 1.8 - For Exercises 27-32, refer to functions s,t,andv....Ch. 1.8 - For Exercises 27-32, refer to functions s,t,andv....Ch. 1.8 - For Exercises 27-32, refer to functions s,t,andv....Ch. 1.8 - For Exercises 27-32, refer to functions s,t,andv....Ch. 1.8 - For Exercises 27-32, refer to functions s,t,andv....Ch. 1.8 - For Exercises 33-36, a function is given. (See...Ch. 1.8 - For Exercises 33-36, a function is given. (See...Ch. 1.8 - For Exercises 33-36, a function is given. (See...Ch. 1.8 - For Exercises 33-36, a function is given. (See...Ch. 1.8 - For Exercises 37-44, find the difference quotient...Ch. 1.8 - For Exercises 37-44, find the difference quotient...Ch. 1.8 - For Exercises 37-44, find the difference quotient...Ch. 1.8 - For Exercises 37-44, find the difference quotient...Ch. 1.8 - For Exercises 37-44, find the difference quotient...Ch. 1.8 - For Exercises 37-44, find the difference quotient...Ch. 1.8 - For Exercises 37-44, find the difference quotient...Ch. 1.8 - For Exercises 37-44, find the difference quotient...Ch. 1.8 - Given fx=4x, a. Find the difference quotient (do...Ch. 1.8 - Given fx=12x, a. Find the difference quotient (do...Ch. 1.8 - For Exercises 47-62, refer to functions f,g,andh....Ch. 1.8 - For Exercises 47-62, refer to functions f,g,andh....Ch. 1.8 - For Exercises 47-62, refer to functions f,g,andh....Ch. 1.8 - For Exercises 47-62, refer to functions f,g,andh....Ch. 1.8 - For Exercises 47-62, refer to functions f,g,andh....Ch. 1.8 - For Exercises 47-62, refer to functions f,g,andh....Ch. 1.8 - For Exercises 47-62, refer to functions f,g,andh....Ch. 1.8 - For Exercises 47-62, refer to functions f,g,andh....Ch. 1.8 - For Exercises 47-62, refer to functions f,g,andh....Ch. 1.8 - For Exercises 47-62, refer to functions f,g,andh....Ch. 1.8 - For Exercises 47-62, refer to functions f,g,andh....Ch. 1.8 - For Exercises 47-62, refer to functions f,g,andh....Ch. 1.8 - For Exercises 47-62, refer to functions f,g,andh....Ch. 1.8 - For Exercises 47-62, refer to functions f,g,andh....Ch. 1.8 - For Exercises 47-62, refer to functions f,g,andh....Ch. 1.8 - For Exercises 47-62, refer to functions f,g,andh....Ch. 1.8 - Given fx=2x+4andgx=x2,...Ch. 1.8 - Given kx=3x+1andmx=1x,...Ch. 1.8 - For Exercises 65-76, refer to function to...Ch. 1.8 - For Exercises 65-76, refer to function to...Ch. 1.8 - For Exercises 65-76, refer to function to...Ch. 1.8 - For Exercises 65-76, refer to function to...Ch. 1.8 - For Exercises 65-76, refer to function to...Ch. 1.8 - For Exercises 65-76, refer to function to...Ch. 1.8 - For Exercises 65-76, refer to function to...Ch. 1.8 - For Exercises 65-76, refer to function to...Ch. 1.8 - For Exercises 65-76, refer to function to...Ch. 1.8 - Prob. 74PECh. 1.8 - For Exercises 65-76, refer to function to...Ch. 1.8 - For Exercises 65-76, refer to function to...Ch. 1.8 - For Exercises 77-80, find fgx and write the domain...Ch. 1.8 - For Exercises 77-80, find fgx and write the domain...Ch. 1.8 - For Exercises 77-80, find fgx and write the domain...Ch. 1.8 - For Exercises 77-80, find fgx and write the domain...Ch. 1.8 - Given fx=1x2,findffx and write the domain in...Ch. 1.8 - Given gx=x3,findggx and write the domain in...Ch. 1.8 - Prob. 83PECh. 1.8 - Prob. 84PECh. 1.8 - For Exercises 83-86, find the indicated functions....Ch. 1.8 - Prob. 86PECh. 1.8 - A law office orders business stationery. The cost...Ch. 1.8 - The cost to buy tickets online for a dance show is...Ch. 1.8 - A bicycle wheel turns at a rate of 80 revolutions...Ch. 1.8 - While on vacation in France, Sadie bought a box of...Ch. 1.8 - For Exercises 91-98, find two functions fandg such...Ch. 1.8 - Prob. 92PECh. 1.8 - For Exercises 91-98, find two functions fandg such...Ch. 1.8 - Prob. 94PECh. 1.8 - For Exercises 91-98, find two functions fandg such...Ch. 1.8 - Prob. 96PECh. 1.8 - For Exercises 91-98, find two functions fandg such...Ch. 1.8 - Prob. 98PECh. 1.8 - Prob. 99PECh. 1.8 - For Exercises 99-102, the graphs of two functions...Ch. 1.8 - Prob. 101PECh. 1.8 - Prob. 102PECh. 1.8 - For Exercises 103-110, refer to the functions...Ch. 1.8 - For Exercises 103-110, refer to the functions...Ch. 1.8 - For Exercises 103-110, refer to the functions...Ch. 1.8 - For Exercises 103-110, refer to the functions...Ch. 1.8 - Prob. 107PECh. 1.8 - For Exercises 103-110, refer to the functions...Ch. 1.8 - Prob. 109PECh. 1.8 - Prob. 110PECh. 1.8 - Prob. 111PECh. 1.8 - Consider a right circular cone with given height...Ch. 1.8 - Prob. 113PECh. 1.8 - Prob. 114PECh. 1.8 - Suppose that a function H gives the high...Ch. 1.8 - Prob. 116PECh. 1.8 - Prob. 117PECh. 1.8 - Given functions fandg, explain how to determine...Ch. 1.8 - Prob. 119PECh. 1.8 - Explain what the difference quotient represents.Ch. 1.8 - Prob. 121PECh. 1.8 - Prob. 122PECh. 1.8 - A car traveling 60 mph (88 ft/sec) undergoes a...Ch. 1.8 - A car accelerates from 0 to 60 mph (88 ft/sec) in...Ch. 1.8 - If a is b plus eight, and c is the square of a,...Ch. 1.8 - If q is r minus seven, and s is the square of q,...Ch. 1.8 - If x is twice y, and z is four less than x, write...Ch. 1.8 - If m is one-third of n, and p is two less than m,...Ch. 1.8 - Given fx=4x2+13, define functions m,n,h,andk such...Ch. 1.8 - Given fx=2x34, define functions m,n,h,andk such...Ch. 1 - For Exercises 1-2, a. Find the exact distance...Ch. 1 - For Exercises 1-2, a. Find the exact distance...Ch. 1 - Determine if the given ordered pair is a solution...Ch. 1 - Prob. 4RECh. 1 - For Exercises 4-6, determine the x-andy-intercepts...Ch. 1 - For Exercises 4-6, determine the x-andy-intercepts...Ch. 1 - Graph the equation by plotting points. y=x22xCh. 1 - Find the length of the diagonal shown.Ch. 1 - Prob. 9RECh. 1 - Prob. 10RECh. 1 - Prob. 11RECh. 1 - Prob. 12RECh. 1 - Prob. 13RECh. 1 - Prob. 14RECh. 1 - Prob. 15RECh. 1 - Prob. 16RECh. 1 - For Exercises 17-18, determine the solution set to...Ch. 1 - For Exercises 17-18, determine the solution set to...Ch. 1 - The table list four Olympic athletes and the...Ch. 1 - For Exercises 20-23, determine if the relation...Ch. 1 - For Exercises 20-23, determine if the relation...Ch. 1 - Prob. 22RECh. 1 - Prob. 23RECh. 1 - Evaluate fx=2x2+4x for the values of x given....Ch. 1 - Prob. 25RECh. 1 - A department store marks up the price of a power...Ch. 1 - Prob. 27RECh. 1 - Prob. 28RECh. 1 - Prob. 29RECh. 1 - For Exercises 29-30, determine the domain and...Ch. 1 - For Exercises 31-34, write the domain in interval...Ch. 1 - Prob. 32RECh. 1 - Prob. 33RECh. 1 - Prob. 34RECh. 1 - Prob. 35RECh. 1 - Prob. 36RECh. 1 - Prob. 37RECh. 1 - Prob. 38RECh. 1 - Prob. 39RECh. 1 - Prob. 40RECh. 1 - Prob. 41RECh. 1 - For Exercises 41-43, determine the slope of the...Ch. 1 - Prob. 43RECh. 1 - Prob. 44RECh. 1 - Prob. 45RECh. 1 - Prob. 46RECh. 1 - Prob. 47RECh. 1 - Prob. 48RECh. 1 - Prob. 49RECh. 1 - Prob. 50RECh. 1 - Prob. 51RECh. 1 - The function given by y=fx shows the value of...Ch. 1 - Prob. 53RECh. 1 - Prob. 54RECh. 1 - Prob. 55RECh. 1 - Prob. 56RECh. 1 - Prob. 57RECh. 1 - Prob. 58RECh. 1 - Prob. 59RECh. 1 - For Exercises 57-63, write an equation of the line...Ch. 1 - Prob. 61RECh. 1 - Prob. 62RECh. 1 - Prob. 63RECh. 1 - A car has a 15-gal tank for gasoline and gets 30...Ch. 1 - A dance studio has fixed monthly costs of $1500...Ch. 1 - Prob. 66RECh. 1 - Prob. 67RECh. 1 - Prob. 68RECh. 1 - Prob. 69RECh. 1 - Prob. 70RECh. 1 - Prob. 71RECh. 1 - Prob. 72RECh. 1 - Prob. 73RECh. 1 - Prob. 74RECh. 1 - Prob. 75RECh. 1 - Prob. 76RECh. 1 - Prob. 77RECh. 1 - Prob. 78RECh. 1 - Prob. 79RECh. 1 - Prob. 80RECh. 1 - Prob. 81RECh. 1 - Prob. 82RECh. 1 - Prob. 83RECh. 1 - For Exercises 79-84, use the graph of y=fx to...Ch. 1 - Prob. 85RECh. 1 - Prob. 86RECh. 1 - Prob. 87RECh. 1 - Prob. 88RECh. 1 - Prob. 89RECh. 1 - Prob. 90RECh. 1 - Prob. 91RECh. 1 - Prob. 92RECh. 1 - Prob. 93RECh. 1 - Prob. 94RECh. 1 - Prob. 95RECh. 1 - Prob. 96RECh. 1 - Prob. 97RECh. 1 - Prob. 98RECh. 1 - Prob. 99RECh. 1 - For Exercises 100-101, use interval notation to...Ch. 1 - For Exercises 100-101, use interval notation to...Ch. 1 - Prob. 102RECh. 1 - Prob. 103RECh. 1 - Prob. 104RECh. 1 - Prob. 105RECh. 1 - Prob. 106RECh. 1 - Prob. 107RECh. 1 - Prob. 108RECh. 1 - Prob. 109RECh. 1 - Prob. 110RECh. 1 - Prob. 111RECh. 1 - Prob. 112RECh. 1 - For Exercises 111-116, refer to the functions...Ch. 1 - Prob. 114RECh. 1 - For Exercises 111-116, refer to the functions...Ch. 1 - For Exercises 111-116, refer to the functions...Ch. 1 - Prob. 117RECh. 1 - Prob. 118RECh. 1 - Prob. 119RECh. 1 - Prob. 120RECh. 1 - Prob. 121RECh. 1 - Prob. 1TCh. 1 - Given x=y4, a. Determine the x-andy-intercepts of...Ch. 1 - Prob. 3TCh. 1 - For Exercises 4-5, determine if the relation...Ch. 1 - For Exercises 4-5, determine if the relation...Ch. 1 - Given fx=2x2+7x3, find a.f1. b.fx+h. c. The...Ch. 1 - Prob. 7TCh. 1 - For Exercises 8-9, write the domain in interval...Ch. 1 - For Exercises 8-9, write the domain in interval...Ch. 1 - Given 3x=4y+8, a. Identify the slope. b. Identify...Ch. 1 - Write an equation of the line passing through the...Ch. 1 - Use the graph to solve the equation and...Ch. 1 - For Exercises 13-16, graph the equation....Ch. 1 - For Exercises 13-16, graph the equation. fx=2x+3Ch. 1 - For Exercises 13-16, graph the equation. gx=x+4+3Ch. 1 - For Exercises 13-16, graph the equation....Ch. 1 - Prob. 17TCh. 1 - For Exercises 18-19, determine if the function is...Ch. 1 - For Exercises 18-19, determine if the function is...Ch. 1 - Prob. 20TCh. 1 - For Exercises 21-26, refer to the functions...Ch. 1 - For Exercises 21-26, refer to the functions...Ch. 1 - For Exercises 21-26, refer to the functions...Ch. 1 - For Exercises 21-26, refer to the functions...Ch. 1 - For Exercises 21-26, refer to the functions...Ch. 1 - Prob. 26TCh. 1 - Write two functions fandg such that hx=fgx. hx=x73Ch. 1 - For fandg pictured, estimate the following....Ch. 1 - Prob. 29TCh. 1 - Prob. 30TCh. 1 - Prob. 1CRECh. 1 - Prob. 2CRECh. 1 - Prob. 3CRECh. 1 - Prob. 4CRECh. 1 - Prob. 5CRECh. 1 - Prob. 6CRECh. 1 - Prob. 7CRECh. 1 - Prob. 8CRECh. 1 - Prob. 9CRECh. 1 - Prob. 10CRECh. 1 - Write an absolute value expression that represents...Ch. 1 - Prob. 12CRECh. 1 - Prob. 13CRECh. 1 - Prob. 14CRECh. 1 - Prob. 15CRECh. 1 - Prob. 16CRECh. 1 - Prob. 17CRECh. 1 - Prob. 18CRECh. 1 - Prob. 19CRECh. 1 - Prob. 20CRE

Additional Math Textbook Solutions

Find more solutions based on key concepts
TRY IT YOURSELF 1 Find the mean of the points scored by the 51 winning teams listed on page 39.

Elementary Statistics: Picturing the World (7th Edition)

Sine substitution Evaluate the following integrals. 7. 05/2dx25x2

Calculus: Early Transcendentals (2nd Edition)

Fill in each blank so that the resulting statement is true. The quadratic function f(x)=a(xh)2+k,a0, is in ____...

Algebra and Trigonometry (6th Edition)

Find the point-slope form of the line passing through the given points. Use the first point as (x1, .y1). Plot ...

College Algebra with Modeling & Visualization (5th Edition)

In Problems 25-32, the graph of a function is given. Use the graph to find: a. The intercepts, if any b. The do...

Precalculus

CLT Shapes (Example 4) One of the histograms is a histogram of a sample (from a population with a skewed distri...

Introductory Statistics

Knowledge Booster
Background pattern image
Calculus
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.
Similar questions
SEE MORE QUESTIONS
Recommended textbooks for you
Text book image
Intermediate Algebra
Algebra
ISBN:9781285195728
Author:Jerome E. Kaufmann, Karen L. Schwitters
Publisher:Cengage Learning
Text book image
Elementary Algebra
Algebra
ISBN:9780998625713
Author:Lynn Marecek, MaryAnne Anthony-Smith
Publisher:OpenStax - Rice University
Text book image
PREALGEBRA
Algebra
ISBN:9781938168994
Author:OpenStax
Publisher:OpenStax
Text book image
Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill
Text book image
Algebra: Structure And Method, Book 1
Algebra
ISBN:9780395977224
Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:McDougal Littell
Text book image
College Algebra (MindTap Course List)
Algebra
ISBN:9781305652231
Author:R. David Gustafson, Jeff Hughes
Publisher:Cengage Learning
SEE MORE TEXTBOOKS
What is a Linear Equation in One Variable?; Author: Don't Memorise;https://www.youtube.com/watch?v=lDOYdBgtnjY;License: Standard YouTube License, CC-BY
Linear Equation | Solving Linear Equations | What is Linear Equation in one variable ?; Author: Najam Academy;https://www.youtube.com/watch?v=tHm3X_Ta_iE;License: Standard YouTube License, CC-BY